フィボナッチ数列
フィボナッチ数列は前の二つの数字を足したものが次の項になる、という数列で以下の漸化式で定義されます。
F_0 = 0, \\
F_1 = 1, \\
F_{n+2} = F_n + F_{n+1} (n ≥ 0)
実際には以下のような
数値になります(第0~21項)
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,
計算方法
前二つの数字を覚えておきさえすればいいので項の小さいほうから計算すれば容易に計算できます
行列累乗
項の小さいほうから計算する場合は第N項を求めるために$O(N)$かかりますが行列累乗という考え方を用いると$O(logN)$で求められます。
少し見方を変えてフィボナッチ数列を以下のような遷移だと考えてみます(図の矢印は加算です)。
やっていることは何も変わらず必要な状態を縦に並べるようにしました
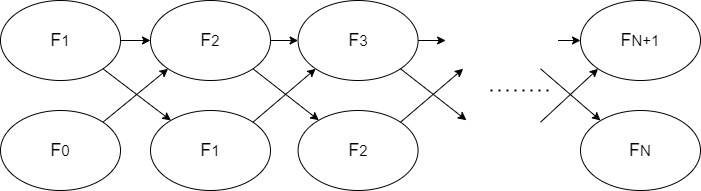
こう考えることで、うまく行列の式に落とし込むことができます
具体的には以下のような式になります
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
F_{n+1} \\ F_{n}
\end{pmatrix} =
\begin{pmatrix}
F_{n + 1} + F_{n}\\ F_{n+1}
\end{pmatrix}
=
\begin{pmatrix}
F_{n + 2} \\ F_{n+1}
\end{pmatrix}
これをもとに2項先は以下のように表現できます(行列は交換則は満たさないが結合則は満たすので好きな順序で計算できます)
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
F_{n+1} \\ F_{n}
\end{pmatrix} =
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
F_{n + 2} \\ F_{n+1}
\end{pmatrix} =
\begin{pmatrix}
F_{n + 3} \\ F_{n+2}
\end{pmatrix}
ここで行列のn乗を求めるために繰り返し二乗法を用いると、$O(logN)$で計算できるというわけです。
※実際には行列のサイズをM × Mとするときに$O(M^3logN)$となります。
ということで、nに0を代入し、m項先を計算する場合以下のように表現できます
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}^{m}
\begin{pmatrix}
F_{1} \\ F_{0}
\end{pmatrix} =
\begin{pmatrix}
F_{m + 1} \\ F_m
\end{pmatrix}
具体例
例えば第8項を計算してみます
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}^{8}
\begin{pmatrix}
F_{1} \\ F_{0}
\end{pmatrix} =
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}^{2^{3}}
\begin{pmatrix}
1 \\ 0
\end{pmatrix}\\
= \begin{pmatrix}
2 & 1 \\
1 & 1
\end{pmatrix}^{2^{2}}
\begin{pmatrix}
1 \\ 0
\end{pmatrix}\\
= \begin{pmatrix}
5 & 3 \\
3 & 2
\end{pmatrix}^{2}
\begin{pmatrix}
1 \\ 0
\end{pmatrix}\\
= \begin{pmatrix}
34 & 21 \\
21 & 13
\end{pmatrix}
\begin{pmatrix}
1 \\ 0
\end{pmatrix}\\
=
\begin{pmatrix}
34 \\ 21
\end{pmatrix}\\
という感じです
第8項は21,第9項は34なので正しく計算できていそうです。