(正の整数の)わり算のあまりのイメージ

　この記事は「十人十色Adventar Advent Calendar 2023」12月17日分です。

　どうも。だまんです。「年齢を考えろ」，というのが今年のテーマでした。今日17日(予定)は誕生日で38歳になりました。あーあ。かれーはつれー。

　なんか若い頃思ってたより加齢って自覚されない。そのわりにセンシティブな話題でもある。体力とかは落ちているんだけど，しかしそれも自覚は薄い。そのために本当になんかやってから，あとでヒヤヒヤする。

　Twitterの名前に(老害)とつけているのは，結構真面目に自分に対して(他人にも)，これ(私)はハイリスク案件おじさんだよと明示しておかないと，忘れるから危険なんですよね。いや，本題と関係ないのでやめとこう。

　さて，いきなりだけど，わり算のあまりの話をします。
　ここ半年くらいあまりに執着している。

　このようなものに執着するのは，子どものころ，わり算が苦手というか嫌いだった¹ことも原因にあると思う。
　どうもわり算というやつはふわふわしてつかみどころがない。

• 結果が一発で決まらず，九九の表の上でスキャンが必要になる(たし算，引き算，かけ算は暗記してれば一発なので)。
• ひとつの計算から，2つの値がでてくるのもなんだかびみょー。
• 「たし算」と「ひき算」はそっくりだけど，「かけ算」と「わり算」はペアなのになんかぜんぜんちがう。

　いまの私の語彙で言うとこういうふうに整理できる。

　というか書いてて思ったんだけど，なんか，前半はほぼ小学校でやることで「別にそれみんな知ってるし」という感じになりそうで怖い。かといって，後半の話は，人によっては突然難しいと感じるかもしれない。あと，無駄に長いし。1人くらいでいいから最後まで行き着く人がが出てくれるといいなあ……。

0 計算のイメージ

　私たちは計算を現実のモデルとしても使うので，そのときは現実の何かと数や演算を結びつけて考える。

りんごが9こあります。
3こずつりんごにまるをつけてわけてみましょう。

🍎🍎🍎　🍎🍎🍎　🍎🍎🍎

　非常にあいまいな記憶だけど，私のわり算のイメージなんかこういう感じだった。
　ただ，リンゴ描くのがめんどうなので，以下ではブロックを使ってますが。

　ところで，ある同じ計算$$A/B=CあまりD$$であってもその$A,B,C,D$の間の関係性は，いくつかの見方(イメージ)があり，それらは切り替えることができる。
　そうすると，描くイメージもかわる。
　まあ，とにかくわり算の「あまり」と「答え」はペアの印象が強いので，これを「あまり」を主役にするだけでも見えるものが変わるのではと期待している。

　前半は図でざっくり説明する。大人の語彙で，小学生のわり算をやる。
　それで，途中からは「あまり」だけに注目することもできて，そうすると，答えを中心としたときとは違うイメージが見える，というような話をする。

1 定義——ある数を引けるだけ引いた回数とあまり

　プログラミング言語では，よくあまりだけ計算する。記号%で10%3と書く。これの結果は，10わる3のあまりだから1になる(10/3は3)。
　で，この、あまりの1とはなんだろうか。なんか，10から3を何度か引いた，残りらしい。という話を手を替え品を替え書くのがこの記事である。

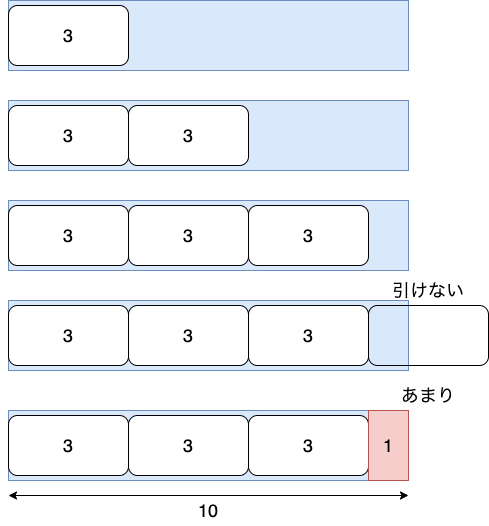
　最初なので，これからこういう図を描くよ，という意味でも図も描いてみましょう。横幅だけ考えてください。青色の部分の幅は10とします。白い3のブロックで埋める(3をひいていく)と3個目でいっぱいになった。この手順によって$10/3=3あまり1$という計算を表現します。

1.1 形式的に

　ここでまず，あまりとわり算(整数の除算・剰余)の定義を(オレオレだけど)，形式的にしておく。興味がなければ飛ばしてもかまわない。ただ，わり算にはいくつかのバリエーションがあるが，割り切れないときはあまりが発生するタイプのわり算だけをここでは扱うということです。
　$1/2=0.5$ではなくて，$1/2=0$あまり$1$である。

《定義 (/)》 ある$1$以上の整数$n$と，$0$以上の整数$m$に対して，
$$m = qn + r かつ 0 ≤ r < n$$
を満たすような $q，r$が一意に存在する。この関係を

• $m / n = q あまり r$

または，

• $m / n = q,$
• $m \% n = r$

と書くことにする²。

《定義おわり》

《定義の説明》まず$m$という数がある。そこから$n$をどんどん引いてみたら$q$回引けた(サイズ$m$の箱の中にサイズ$n$のブロックが$q$個入ったとも言える)。そして，すきまができたら，これをあまり$r$と呼ぶ。

　細かい話だが「引けるだけ」というのは1つのポイントで，定義だと「すきま(あまり)がnより小さくなるように($0 ≤ r < n$)」という部分が担当している。
　もし，このルールがないと中途半端に引いたり引きすぎてもいいことになるので，わり算の答え$q$とあまり$r$のペア$(q, r)$がいろいろあることになってしまう(一意でない)。

　小学生くらいだと，私たちはわり算あってのあまりというか，ペアで使ったと思う。しかし，わり算の「答え」は見ずに，あまりだけを使うこともできる。

2 あまりだけを見る(1): 奇数・偶数の足し算の奇・偶

　そういえば，奇数と偶数って何なんだろうね。あちこちの文明にあったようなのだけど。まあいいか。

　まず，そもそもどういう問題を考えるか確認すると，「ある整数$m$，$n$があって(もちろん奇数か偶数のどちらかわかっている)，$m + n$が奇数か偶数か知りたい」という感じ。ちなみに答えがこうなのは，どうせみんなわかっていると思います:

• 奇数+奇数=偶数
• 奇数+偶数=奇数
• 偶数+偶数=奇数　

　中学では，(ある整数$n$を使って)偶数は$2n$，奇数は$2n+1$と書ける(定義できる)と習った。そして奇数・偶数の和が何になるか，これらの式を直接足して，数式変形パワーでうまいこと$2N$または$2N+1$の型にはまるか調べた。
　ただ，これは数式変形パワーを使うので，なんでこうなるんだという納得感があったかというと人によると思う(そもそも納得感のためにやっていることでもない)。

　しかし，この判定法は，数式の「かたち」で判定するので，ちょっとプログラムで表現するにはめんどくさい。そこで，奇数と偶数の定義を次のように言い換えたい。
　ある整数$m$があって，もし$m$を$2$でわってみて，あまり$m%2$が$0$なら偶数，$1$なら奇数である。

《定義 (奇数・偶数)》

• $m$は奇数: $m\%2=1$のとき
• $m$は偶数: $m\%2=0$のとき

　プログラミングではふつう具体的な値についての奇偶の判定をするので，あまりで書く方が都合がいい。この判定はプログラミング教育ではわりとよく用いられる。

　これを使って，「納得感」を出したい。どうしたら「納得感」がでるだろうか。
　さて，そんなことを考えていたら，ちょうどよく次のツイートを見た。よしパクろう。

まず，奇数と偶数は，ブロックの言葉になおすと，

• 奇数: 2のブロックで埋めて，あまり(すきま)が1
• 偶数: 2のブロックで埋めて，あまり(すきま)がない(0)

ということになる。

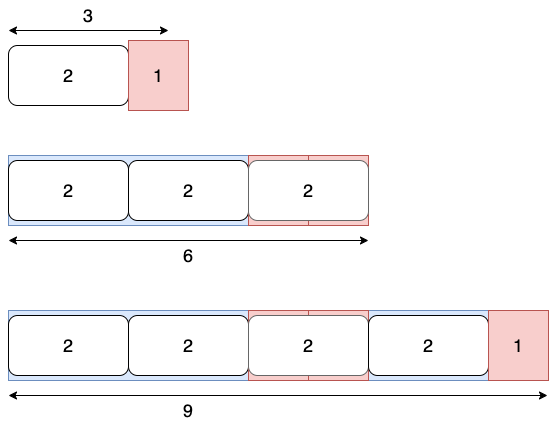
下の図は，さきほどのツイートの前半で言っていたことを再現したものだ。3に3をいくつか加えていったものを，それの奇偶を見るために2でわっている。

• $3/2=1あまり1$
• $(3+3)/2=2あまり0$
• $(3+3+3)/2=4あまり1$
• $(3+3+3+3)/2=4あまり0$

いま，奇数・偶数の判定に白いブロックは関係ないので，赤いのがくっついているか(あまり)だけをみる。

• 奇数: 赤ブロック1個
• 偶数: 赤ブロック0個

　奇数である3を2個，3個と足していくと，あまりだったものが蓄積していく。
　このとき，とりあえず，白いブロックは見ない。赤だけを見る。

　$+3$すると，赤いブロックがちょうど1個たされる。
　しかし2個たまると同時に白い2ブロックにになる。ノーカウントになる。

これはわり算の定義(/)で，引けるぶんがあったら全部引け(あるいは白いブロックが入るすきまがあれば，白いブロックをつめろ)と決めたからだ。
　こうしてすきまが消えた場合は，赤(あまり)が0なので偶数ということになる。
　めんどくさくて図をちょっとしか描いてないけど，5個以上の3の和でも，赤ブロックは1個ずつ増えるので，和は交互に奇数と偶数になる。

これを赤ブロックの個数で書く。ただし，$2\%2=0$。

• 3は……1
• 3+3は……(1+1)%2=0
• 3+3+3は……(1+1+1)%2=1
• 3+3+3+3は……(1+1+1+1)%2=0

　書き方が妙な感じで申し訳ないんだけど。

　で，これは奇数・偶数全体に一般化できる。

• 奇数: 赤ブロック1個
• 偶数: 赤ブロック0個

と定義したのだったから，2でわったあまり(赤ブロック)だけ見ればいいので，3だけでなく，奇数・偶数一般の組み合わせを検討できる。

となる。

こういうタイプの2で割ったあまりしか見ない演算は数学の書き方だと，

• $1+1\equiv 0\mod 2$
• $1+0\equiv 1\mod 2$
• $0+0\equiv 0\mod 2$

というふうに書き，「法2のもとで2と0は合同」とかいいます。初めて見たときどこで区切るのかわからなかった記憶がありますが，$\mathrm{mod}\quad2$はいわば注意書きで，両辺を別々に2でわってあまりをとるよ……という感じなんだと思います。
　奇数と偶数は下記のように，2でわったあまりが等しいグループとして書けます(ゼロは偶数じゃないんだけど)。さっきの赤いブロック記法は一番左の0，1を偶数と奇数の代表として使ったわけです(本当は偶数代表を4と奇数代表を107とか適当な数で代表できます: $4+107=111$で，$111\equiv1\mod 2$だから偶数＋奇数=奇数)。

• $1\equiv 3\equiv 5\equiv 7\equiv 9……\mod 2$
• $0\equiv 2\equiv 4\equiv 6\equiv 8\equiv 10……\mod 2$

3 あまりだけを見る(2): 時刻，周期性

　まだあるのかよ……と思うよね……。
　そもそも，本稿は書き始めたとき，AtCoderで使うようなわり算とあまりを使うネタをすべて網羅するというテーマだったので長いのである。

　さきほどは偶数・奇数の判別のために，$n\%2$が$1$か$0$かを調べた。それによってnを奇数・偶数というカテゴリーにわけた。
　つまり，あまりだけを見るということをしたわけである。 
　これを$n\%3$，$n\%4$，……のようにするとどうなるか。

　ちょっと話が飛ぶけど，12時間(0:00〜11:59)の記法で，10:22の1時間後の時刻を考える。
　これは11:22である。
　じゃあ，その14時間後は？
　25:22と答えても夜勤か深夜アニメ方面だとマルになる。お疲れさまです。しかし，ここでは1:22になるということにしたいんですね。
　この計算は12でわったあまりだけを見ていると言える。日付や午前午後，あと分以下の部分は省略して，時刻だけを見ると，

$$(11+14)\%12=1$$

　大げさないいかたをすると，このルールは「いま」と「この後12時間ごとにくる瞬間」を同一視する。

図を描くのがめんどくさくなってきて，ウィキメディアコモンズから借りてきました。

• 左: $9\%12=9$
• 右: 4時間後は$(9+4)\%12=13\%12=1$

by Spindled (CC 表示-継承 3.0 非移植)

　こういうのを周期性があるという。ルーレットやスロットマシンのドラムのように，ぐるぐる回って何週目かを考慮しない世界。

　ちなみに我々になじみのある例では10進数の最下位の桁がある(厳密には任意の1桁)。ここだけ見てみると同様のことが言えて，$n\%10$の世界になっている。なぜでしょうか。

4 n進表記の「10」で割ったあまり

　そろそろ脱落してだれも読む人がいなくなったんじゃないかと思うから，趣味に走るが……。

　プログラミングの課題で，「標準入力から7進数の整数を与える。これを63進数の整数に変換し標準出力に出力しなさい。」と言われたらどうしますか。結構地獄じゃないですか。私は某所でそういう課題があってうぉああああってなった。
　ここでやりたいのはそういう話です。
　63進数というのは大変だから，10進数でやってみて，その後n進数についてみてみる。

4.1 10進表記の10で割ったあまり

10進数の「一の位」は，10の周期で0に戻る。
　これは，2桁の数$n$を考えると，「十の位」は$n$の中に10がいくつ含まれているかを書く場所で，「一の位」は10未満の数を書く決まりだからだ。

　幅10の白いブロックのイメージして$n$にがんがんつめて，あまりが一の位なので，$n\%10$。

　たとえば10進数の42を10でわります。ついでに答え(商)をどんどん10でわっていくことにします。

• $42/10=4あまり2$ (一の位)
• $4/10=0あまり4$ (十の位)
• (商が0になったのでおわり)

　もっと大きい数でやってみるほうが桁が右から取り出される様子がわかりやすい。12345だと，

• $12345/10=1234あまり5$ (一の位)
• $1234/10=123あまり4$ (十の位)
• $123/10=12あまり3$ (百の位)
• $12/10=1あまり2$ (千の位)
• $1/10=0あまり1$ (万の位)
• (商が0になったのでおわり)

　桁によって表現する方法の定義はn進数に拡張できるので，「n進数の10(10進数のn)でわった答えとあまり」をもちいる方法は，ほかのn進表記でも成り立つ。
　これは数の性質というよりも，表記法の性質を利用している。

　また逆に，各桁の数字が列として$1,2,3,4,5$のように与えられたとき，もとの値にもどすには，定義(/)を思いだすと($(答え)×10+(あまり)=(わられる数)$)なので，

• $0×10+1=1$
• $1×10+2=12$
• $12×10+3=123$
• $123×10+4=1234$
• $1234×10+5=12345$

のようにする。プログラムっぽく書くと，m=m*10+n[i]($i$は列の要素のインデックス)をくり返す感じ。

• n進表記の「10」で割る: n進表記の一番下の桁が消える
• n進表記の「10」で割ったあまり: n進表記の一番下の桁

4.2 n進表記の「10」で割ったあまり

　最後に，さっき書いた問題，「標準入力から7進数の整数を与える。これを63進数の整数に変換し標準出力に出力しなさい。」の解答を書く。標準入力と標準出力は原則的には文字列であるから，ここでは文字列型の変数で代用する。
　まず63進数の数字を63個設定する必要がある。0〜9はそのまま使う。以降の数字はa,b,c,……,zで表し，そのあとはA,B,C,……,Z,空白文字，とする(63個)³。
　なお，7進数は0〜6を使う。

　話が長くなりそうだから，先にプログラムを貼っておきます(Google Colab.)。前半が解答例。後半のセルは逆方向に計算します。

　普段は気にしなくてもいいのだが，一般的なプログラミング言語(一般的なパソコンのCPU)の整数型は，内部的には2進数で，printf()やprint()のような機能が勝手に10進表記などに変換してくれている。
　値として変数に入っているのはすべて2進数だから，n進数からm進数にするときは，2進数を経由する。

　2・8・10・16進表記の文字列と整数型の値は簡単に変換できるが，しかし，7進とか63進とか，へんてこりんな表記にする場合は何か工夫が必要になる(簡単にできる8進数を外したのはわざと)。
　とりあえず，文字列型の変数str7に入力として7進表記の整数"320530021212060461464463102020"が入っている。さきほど言ったように文字列型を使う。
　先に文字列(数字の列)から数を復元し，2進にする。その後2進数の整数から桁ごとに取り出す。さきほどの説明とは逆の順番になっている。

　リテラルとして7進数の「10」を書けないので，これを10進数の7で書いている(n*7のところ)。あと，int()は文字をint型整数に変換する。これはちょっとずるいのだが，7進表記の1桁分を10進として変換している(16<nなn進数表記になると使えない)。

#input string
str7 =  "320530021212060461464463102020"

n = 0
for ch in str7:
    n = n*7 + int(ch)

str63=""
while n != 0:
    m = n % 63
    n = n // 63
    str63 += d63[m]
print("str63:", str63[::-1])

　さて，これで整数型の値になったので，次はn進表記を文字列として作っていく。ここでなぜ文字列にしないといけないかというと(略)。
　63進数の「10」は63なので，63でわっていくだけだ。d63というやたら大きいリストがあるが，これは63進表記で使う数字が並べてあって，d63[m]のようにするとm番目の数字が出てくる。というわけで，出力をひっくり返して表示すると，63進表記の値が出る([::-1]というのは文字列str63を配列のように扱っている。反転したものになる)。

str63: Happy Holidays

オチ

ABC(AtCoderの一番簡単なコンテスト)の334回目があり、C問題にここに説明した内容を負の整数に拡張したものが出て、ものの見事に解けませんでした……。

付録 AtCoderで整数のわり算を使う例

• 「倍数」だから割ればいい……わけではない: https://atcoder.jp/contests/aising2020/tasks/aising2020_a
• (解説)をみるとまさにあまり！: https://atcoder.jp/contests/abc266/tasks/abc266_b

1. 私は，どうも小学校とにかく暗記と反復練習が嫌いで，授業中の演習も結構サボってしていたし，計算ドリルや問題集なんかをやったことがないので，教育に問題があるとかそういう話ではない。 ↩

2. 除法 - Wikipediaを参考にしていたが，だいぶ変更している。 ↩

3. この63進数というのは，実は一応意味があって，数字(10文字)とアルファベット(大文字26文字＋小文字26文字＋空白文字)をフルに使うとこうなる。 ↩