はじめに
この記事では,ビットコインの基本的な仕組みを学んで,その技術に入門してみたいと思います.基本的な仕組みといってもひとつの記事で説明するには量が多すぎるので,内容を分割し,以下のように 3つの記事として書いています.
- トランザクション編
- データ構造・マイニング編(この記事)
- ネットワーク編
「入門」の目安として,ビットコインの送金の仕組みが理解できることを目標にします.一連の記事を通して考える具体的な設定として,以下の状況を想定します.
- アリスがボブに 1BTC を送金する.
また,最初からすべてを正確に説明しようとすると,たくさんの新しい概念をいっぺんに突きつけることになり,入門者を張り倒してしまいかねないので,簡単のため適宜ウソの説明をします(たとえば,中央集権的なビットコインの管理者が登場したりします).ウソの説明は新しい概念を導入するに従って徐々に訂正し,一連の記事の最後にはウソのない正確な仕組みをお目にかけられるよう努めます.
前回「トランザクション編」を経て,ビットコインの送金が次のように行われるところまで理解できたことになっています.
| ビットコインの送金(ver.2) |
|---|
| ${\texttt 1.}$ アリスがボブに 1BTC を送金するトランザクションを用意する. ${\texttt 2.}$ アリスがトランザクションに署名し,自分の公開鍵と併せて提示する. ${\texttt 3.}$ ビットコインの管理者がトランザクションを検証する. ${\texttt 4.}$ ビットコインの管理者がトランザクションを台帳に追記する. |
今回の記事では,ビットコインの台帳を実現するデータ構造と,ビットコインのマイニングの仕組みを紹介します.
言い訳
これは「データ構造とアルゴリズム Advent Calendar 2019」20日目の記事です.アドベントカレンダーにもかかわらず,いきなりタイトルに 2/3 などと書かれた続編記事を投稿してしまいました.ごめんなさい.以下はその言い訳です.
- もともとビットコインのデータ構造について書くつもりだった.
- しかし,トランザクションの仕組みを知っていないと厳しいということに思い至った.
- せっかくだからビットコインの基本的な仕組みから入門記事を書こうと思った.
- 記事が長くなりすぎてうんざりしてしまうので内容を分割した.
- トランザクションの話が長くなり,肝心のデータ構造の話が 2/3 に追放された.
データ構造自体は,トランザクションについて詳しく知らなくても理解できるよう配慮したつもりですが,当然知っていたほうがイメージしやすい部分が多いはずなので,忙しくなければ前回「トランザクション編」から読んでほしいなぁと思います.
あ,トランザクションというのは送金取引のことです.
基礎技術の準備
暗号学的ハッシュ関数
以下の性質をすべて満たす数学的な関数を **ハッシュ関数(hash function)**と言います.
- 任意の長さの入力に対して,出力が固定長である.
- サイズ $n$ の入力に対して,$O(n)$ 時間で出力を計算可能である.
以降,記号 $H$ でハッシュ関数を表し,入力 $x$ に対する出力 $H(x)$ を $x$ のハッシュ値と呼びます.
一般に,ビットコインを含む多くの仮想通貨では,ハッシュ関数として通常のハッシュ関数により強い制約を加えた **暗号学的ハッシュ関数(cryptographic hash function)**を用います.暗号学的ハッシュ関数とは,以下のすべての性質をみたすハッシュ関数です.
-
衝突耐性(collision resistance):
衝突するハッシュ値の発見が困難であるという性質.すなわち,$x \neq y$ かつ $H(x) = H(y)$ であるような入力の組 $(x, y)$ を見つけることが困難であるという性質. -
秘匿性(hiding):
ハッシュ値から入力を特定することが困難であるという性質.すなわち,$y = H(r||x)$ であるときに,$y$ と $H$ から $x$ を特定することが困難であるという性質.ここで,$r$ は min-entropy の高い確率分布から選ばれた秘密の値.記号 $||$ は連結を表す. -
パズル親和性(puzzle friendliness):
ハッシュ値から入力の一部を特定するために,多くの計算コストを要するという性質.すなわち,ハッシュ関数の $n$-bit の出力 $y = H(k||x)$ に関して,$y$,$k$,および $H$ から $o(2^n)$ 時間で $x$ を特定することが困難であるという性質.ここで,$k$ は min-entropy の高い確率分布から選ばれた値.
この記事で使う「困難」あるいは「簡単」という言葉は,膨大な時間的・空間的コストを伴う,あるいは伴わないことを意味します.
以降,ハッシュ関数と言ったらすべて上記性質をみたす暗号学的ハッシュ関数を意味するものとします.ビットコインでは,ハッシュ関数として SHA-256 を利用しています.
ハッシュポインタ
**ポインタ(pointer)**とは,あるオブジェクトの格納先を示すものです.より正確に言えば,ポインタとはあるオブジェクトを一意に識別するための ID であり,その ID として対象オブジェクトにアクセス可能な論理的位置情報(アドレス)を用いたものです.
**ハッシュポインタ(hash pointer)**とは,オブジェクトを識別するための ID として対象オブジェクトのハッシュ値を用いたポインタです.すなわち,オブジェクト $x$ のハッシュポインタは $H(x)$ となります.いま,$H$ は衝突耐性をみたす暗号学的ハッシュ関数なので,$H(x)$ は $x$ を一意に識別するための ID として十分に機能することが期待できます.
ブロックチェーン
以下の性質をみたす(一方向)連結リストを **ブロックチェーン(blockchain/block chain,または hash chain)**と言います.
- 各ノードがデータを格納するオブジェクトと1つのハッシュポインタから成る.
- 各ハッシュポインタは自身の1つ前のノードを指す.
要するにブロックチェーンとは,連結リストのポインタをハッシュポインタに置き換えたものです.いま $i$番目のノードを構成するオブジェクトとハッシュポインタをそれぞれ $x_i$ と $p_i$ としたとき,$p_{i+1} = H(p_i||x_i)$ が成り立ちます.一般に,ブロックチェーンにおいて各ノードは **ブロック(block)**と呼ばれ,以降でもこの名称を用います.
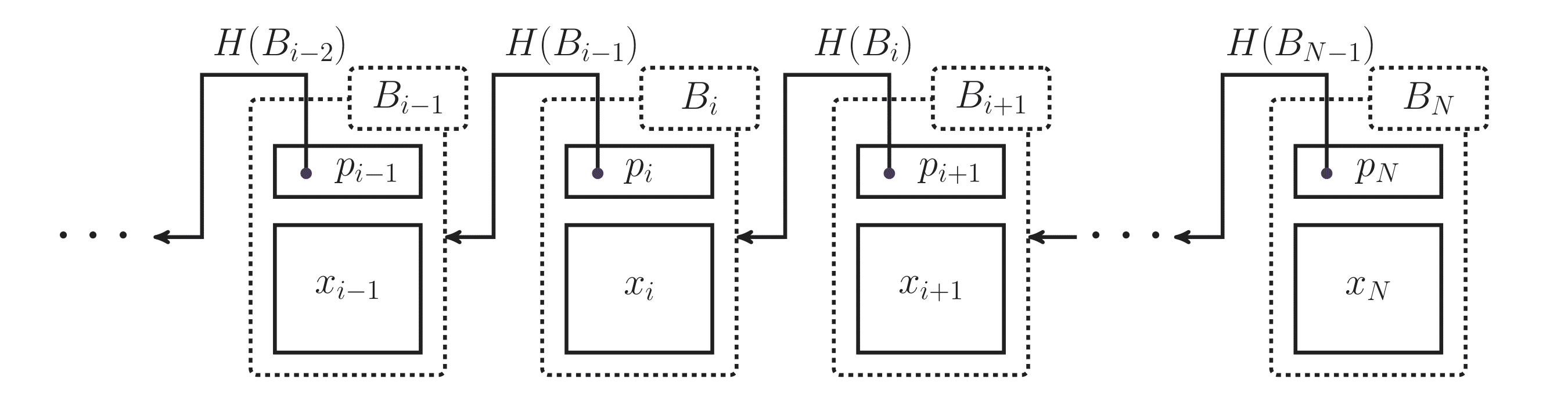
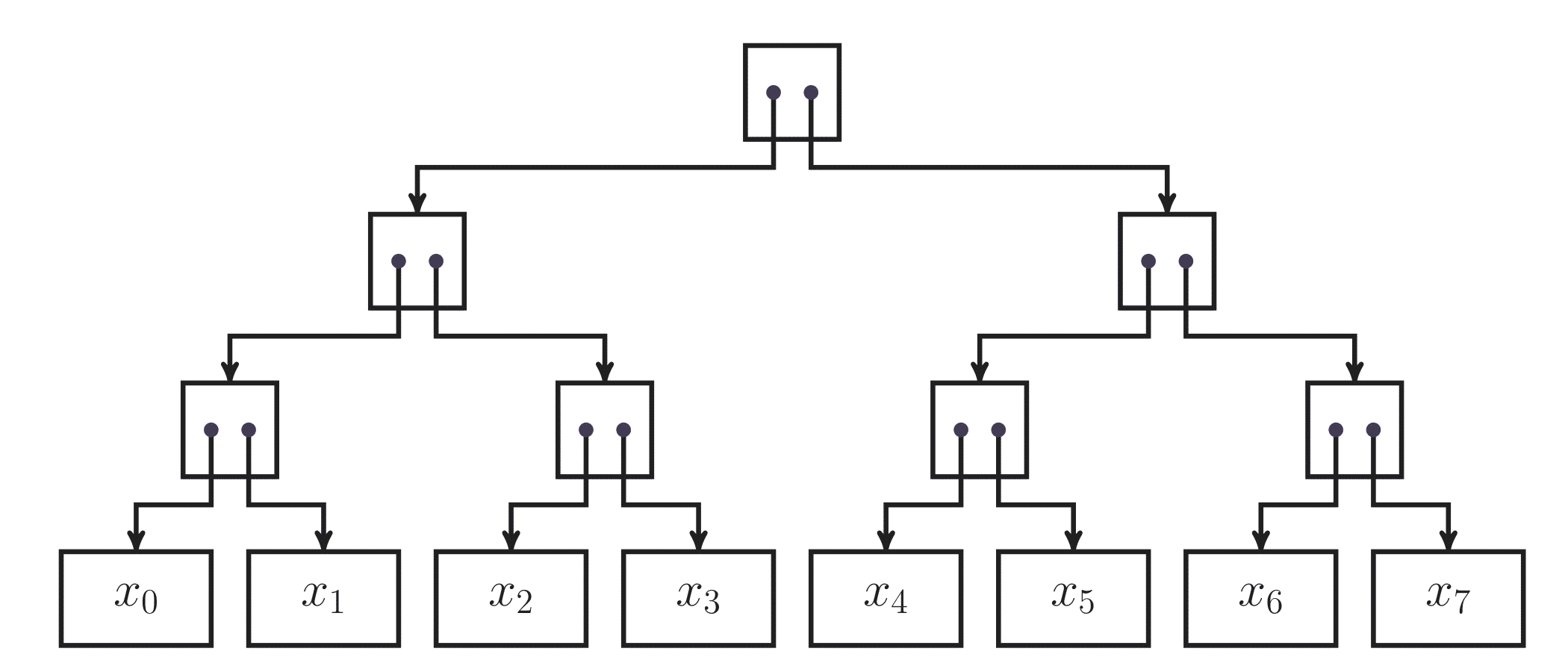
図 1:ブロックチェーン.各 $B_i$ はブロックを表し,$B_i=p_i||x_i$.$B_N$ は先頭(最新)ブロック.矢印はハッシュポインタの示す先を可視化したもの.
Merkle tree
以下の性質をみたす二分木を **Merkle tree(または hash tree)**と言います.
ビットコインのデータ構造
前回の記事「トランザクション編」で,ビットコインの台帳について説明しました.台帳は,ビットコインの承認されたトランザクションを必要十分に記録したものです.ビットコインのデータとは,すなわちこの台帳のデータであると考えることができます.このことから,以降,この台帳を指してビットコインと言うことがあります.本記事で考えるビットコインのデータ構造とは,この台帳のデータ構造のことです.
全体の構成(ブロックチェーン)
前回の記事「トランザクション編」では,簡単のため,台帳を以下のようなテーブル構造で考えました.
| ID | Contents | Public key |
|---|---|---|
| 0 | $p_0$ による署名済みのトランザクション内容 | 公開鍵 $p_0$ |
| 1 | $p_1$ による署名済みのトランザクション内容 | 公開鍵 $p_1$ |
| 2 | $p_2$ による署名済みのトランザクション内容 | 公開鍵 $p_2$ |
| $\cdots$ | $\cdots$ | $\cdots$ |
| $n$ | $p_m$ による署名済みのトランザクション内容 | 公開鍵 $p_m$ |
図 3:簡単な台帳の様子.
しかし,こうした機構では以下のような問題があります.
- 過去のデータを簡単に改竄できる.
- データの完全性確認のためのコストが大きい.
まず,言うまでもないことですが,過去のデータが簡単に改竄されるようでは,台帳は意味を成しません.
ビットコインのトランザクションの仕組み(前回「トランザクション編」を参照)を鑑みれば,台帳には新しいトランザクションの追加のみができればよく,過去のすでにあるトランザクションを編集したり削除したりする必要はありません(むしろできないほうが望ましく,過去データの編集はすなわち改竄と見なすべきです).したがって台帳には,台帳にすでに存在するトランザクションに後から手を加えることが困難で,新しいトランザクションの追加のみが効率よく行えるデータ構造を用いると良さそうです.
次に,テーブル構造のようなモデルでは,データの完全性の確認を効率よく行うことができません.平たく言えば,台帳が改竄されていないことを簡単に確認できないということです.ただトランザクションが羅列されているようなデータ構造では,完全性の確認のためにすべてのトランザクションの整合性をひとつずつ検証する必要があり,膨大なコストがかかります.
こうした問題に対応するため,ビットコインはブロックチェーンで台帳を構築しています.各ブロックはトランザクションを含みます.新しいトランザクションは新しいブロックに包含され,ブロックごと追加される形で台帳に追記されます.
上で見たような改竄にまつわる問題は,ブロックチェーンの最新ブロックのハッシュポインタを監視しておくことで解決できます.たとえば,あるブロック $B_i$ に含まれるトランザクションを編集すると,ブロック $B_i$ の値が変わり,そのハッシュ値も変わります.これは,次の(ひとつ新しい)ブロック $B_{i+1}$ が持つハッシュポインタ(これは $B_i$ を指す)の値が変わることを意味します.これはブロック $B_{i+1}$ のハッシュ値にも影響を与えるため,その次のブロック $B_{i+2}$ の持つハッシュポインタの値も変わります.ハッシュポインタの値の変更は連鎖的に以降すべてのブロックに発生し,当然,最新ブロックのハッシュポインタも変更されます.したがって,最新ブロックのハッシュポインタを監視されているだけで,すべてのトランザクションの改竄が困難になります.これは同時に,最新ブロックのハッシュポインタを確認するだけで,それまでのブロックのデータの完全性を検証できることを意味します.
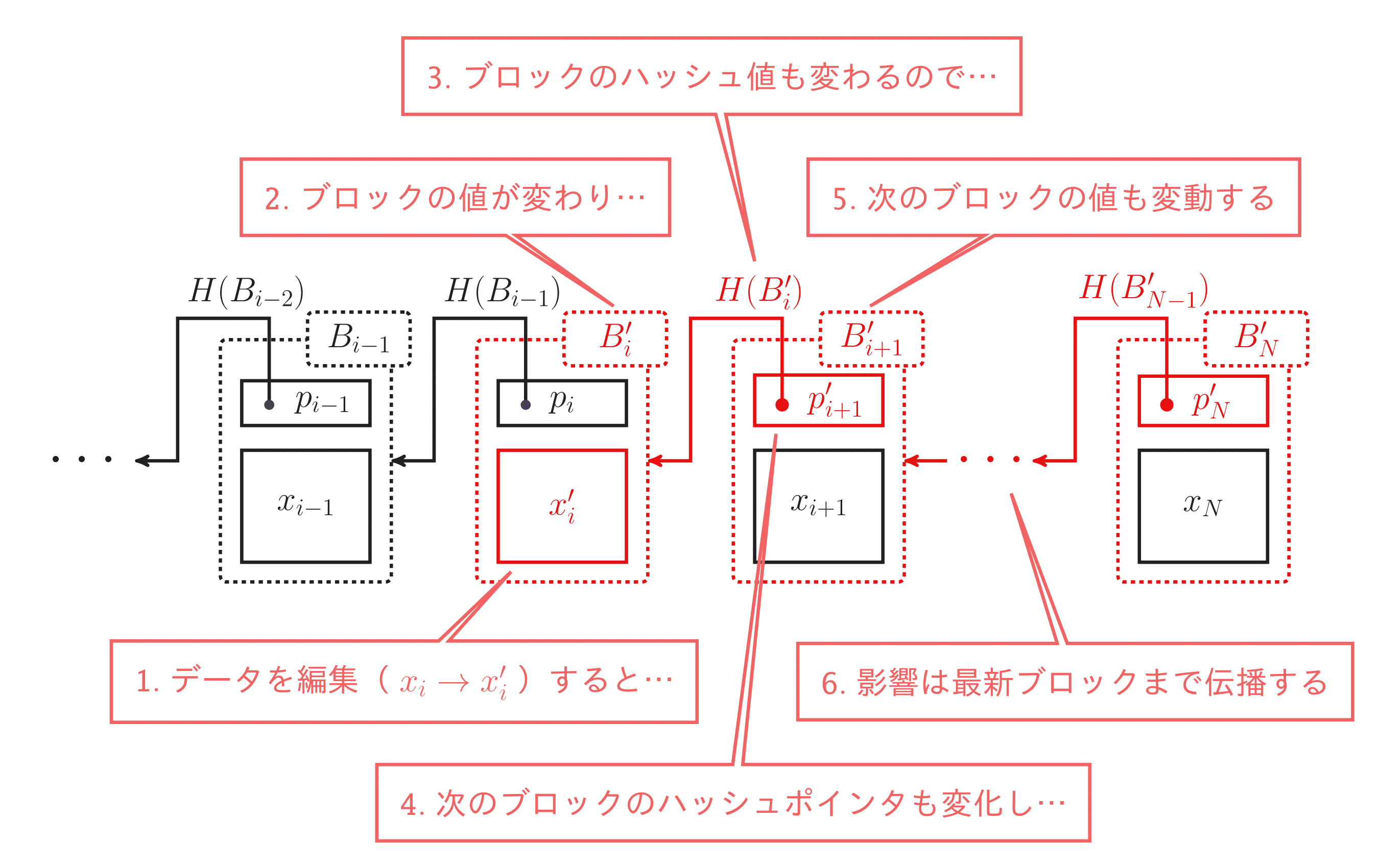
図 4:ブロックチェーンの改竄耐性.
各ブロックの構成
ブロックチェーンの各ブロックはトランザクションを含むと言いましたが,それ以外にもいくつか情報を含みます.具体的には,各ブロックは以下の要素から構成されます.
- ハッシュポインタ:直前のブロックを示すハッシュポインタ.
- ナンス(nonce):32-bit の値.詳細は後述.
- Merkle tree:正確には Merkle tree の根ノード.
肝心のトランザクションが見当たりませんが,これは Merkle tree に含まれています.実際のところ,トランザクションは各ブロックにひとつではなく,いくつかのトランザクションが平衡な Merkle tree を用いてまとめてブロックに記録されています.ブロックチェーンへの(つまり台帳への)追記も,ブロックの追加に伴っていっぺんに行われます.複数のトランザクションをブロックにまとめて処理することには,承認を高速化しつつ,ブロックチェーンが手に負えない速度で成長するのを防ぐ意味があります.
トランザクションは,下図に示すように Merkle tree の葉ノードとして保持されます.
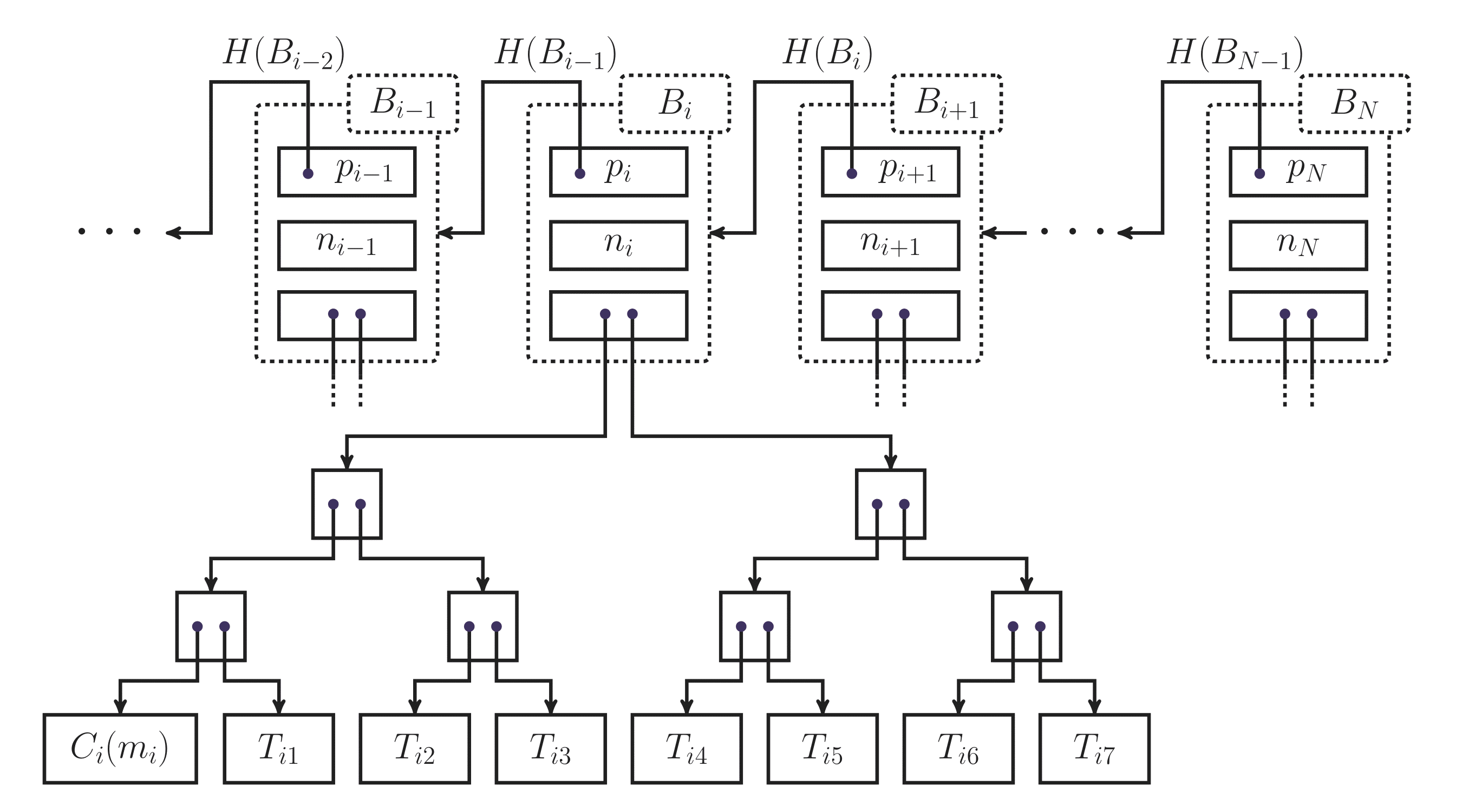
図 5:ビットコインのデータ構造.各 $n_i$ はブロックのナンス.矢印はハッシュポインタの示す先を可視化したもの.$T_i$ と $C_i$ はブロック $B_i$ の Merkle tree に包含されるトランザクションとコインベーストランザクション.$m_i$ はコインベーストランザクション $C_i$ が持つナンス.
ここで気をつけたいのが,各 Merkle tree にはひとつだけコインベーストランザクションが含まれるということです.Merkle tree は各ブロックにひとつ含まれるので,各ブロックにひとつのコインベーストランザクションがあることになります.コインベーストランザクションとは,新しいコインを発行するためのトランザクションでした(前回「トランザクション編」参照).また,「トランザクション編」では説明していませんでしたが,コインベーストランザクションは入力と出力の他にナンスをひとつ持ちます.ブロックのナンスと同様,これも 32-bit の値です.これらナンスの役割については,以下「ビットコインのマイニング」で紹介します.
いま,ブロックチェーン側から見ると,トランザクションは直接ブロックに保持されるわけではなく,Merkle tree を介して間接的に保持されることになりました.この場合でも,上で考えた台帳の改竄耐性が損なわれることはありません.Merkle tree もハッシュポインタを用いたデータ構造であり,葉ノードのトランザクションを編集すれば,その影響が根ノードの値まで伝播します.これにより,ブロック中のデータが変更されるため,ブロック自体のハッシュ値にも影響を及ぼすからです.
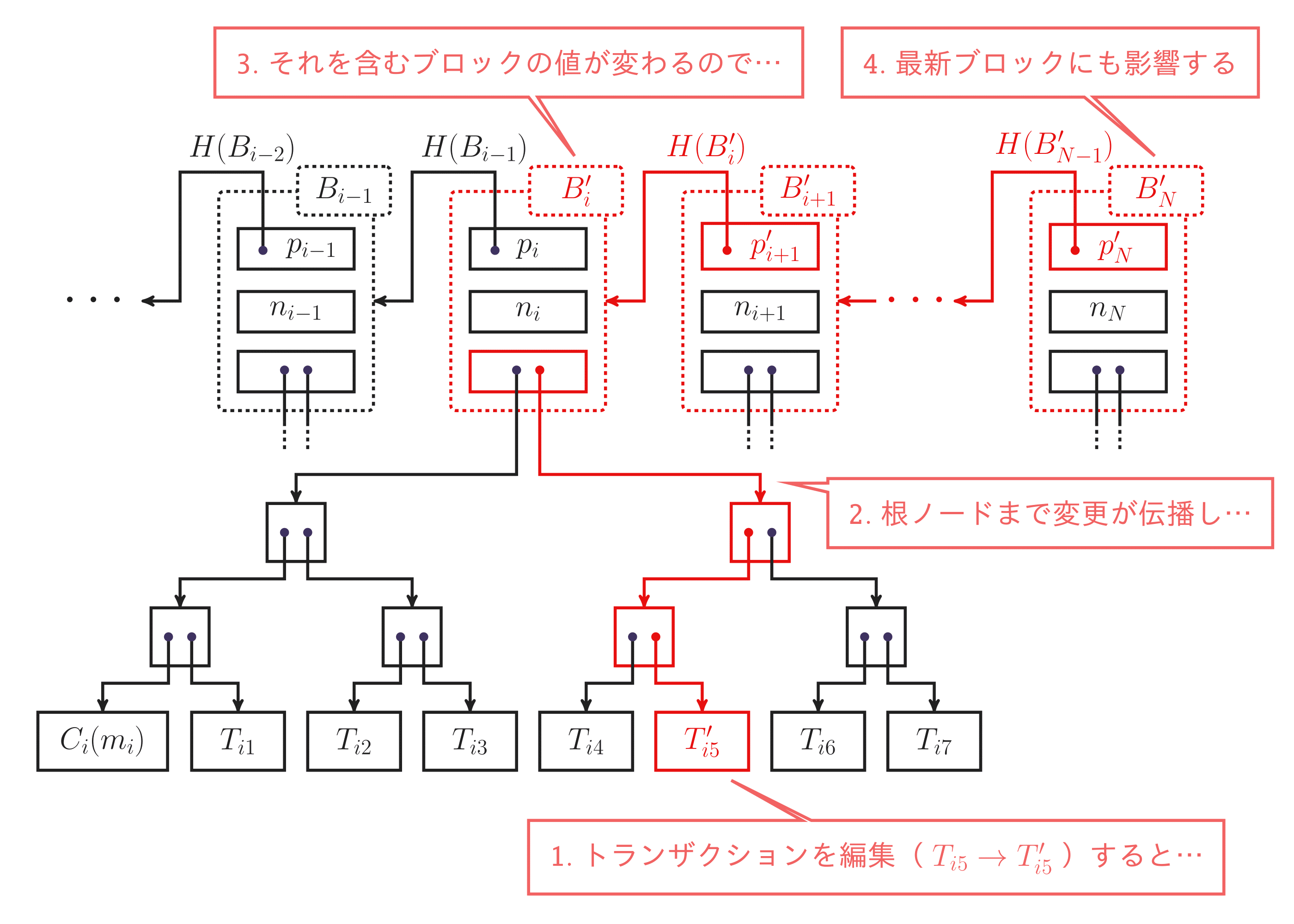
図 6:ビットコインの改竄耐性.
ビットコインのマイニング
新しいブロック
ビットコインのデータ構造がわかったところで,台帳のブロックチェーンに新しいブロックを追加することを考えてみます.これは以下のようにして実現できます.
- 誰かが新しいブロックを提示する.
- ビットコインの管理者が提示されたブロックを承認する.
これは,前回「トランザクション編」で紹介したトランザクションの処理と非常に似ています.ただ,トランザクションはアリス(送金者)が提示する必要がありましたが,ブロックは誰でも提示できます.もちろん,アリスが自分で提示しても構いません
前回までの知識で,ビットコインの送金は以下のように行われると説明していました.
| ビットコインの送金(ver.2) |
|---|
| ${\texttt 1.}$ アリスがボブに 1BTC を送金するトランザクションを用意する. ${\texttt 2.}$ アリスがトランザクションに署名し,自分の公開鍵と併せて提示する. ${\texttt 3.}$ ビットコインの管理者がトランザクションを検証する. ${\texttt 4.}$ ビットコインの管理者がトランザクションを台帳に追記する. |
新しいブロックの追加は,上記 ${\texttt 3.}$ と ${\texttt 4.}$ のプロセスに該当します.ブロックの提示者は正しいトランザクションを選定してブロックに含め,管理者はトランザクションの正当性も含めてブロックの有効性を検証し,有効と認めれば,それを新たなブロックとして台帳のブロックチェーンに追加します.
ブロックチェーンやブロックという概念を知ったいま,ビットコインの送金プロセスを改めて少し詳しく書き直すと,次のようになります.
| ビットコインの送金(ver.3) |
|---|
| ${\texttt 1.}$ アリスがボブに 1BTC を送金するトランザクションを用意する. ${\texttt 2.}$ アリスがトランザクションに署名し,自分の公開鍵と併せて提示する. ${\texttt 3.}$ 誰かがアリスのトランザクションを含めたブロックを提示する. ${\texttt 4.}$ ビットコインの管理者がブロックを検証する. ${\texttt 5.}$ ビットコインの管理者がブロックをブロックチェーンに追加する. |
前回「トランザクション編」と同様,簡単のため,権限を持つ誰か特定の人物がビットコインシステムを管理しているように話す場面があります.上でも「ビットコインの管理者」と書いていますが,実際にはビットコインは非中央集権的な分散システムで管理されており,ユーザーは誰もが管理者としてシステムに参加できます(これについては,次回「ネットワーク編」で紹介したいと思います).
ブロックが有効である,つまり,新しいブロックとして承認されブロックチェーンに追加されるためには,必要なことが2つあります.
- まず,含まれるトランザクションがすべて正しい必要があります.トランザクションの正当性に関しては,前回「トランザクション編」で紹介しました.ブロックの提示者は,人々が次々と提示するトランザクションから正しいものをいくつか選定し,それらを用いて Merkle tree を構築します.
- 次に,ブロックのハッシュ値がある条件をみたす必要があります.1. も併せてより厳密に記述すると,以下のようになります.
| 有効なブロック |
|---|
| $k$ をある非負整数とし,最新のブロックを指すハッシュポインタを $p$,コインベーストランザクションのナンスを $m$,Merkle tree の根ノードを $M(m)$,ブロックのナンスを $n$ とする.Merkle tree は正しいトランザクションのみから成るとする.ここで,$p$,$M(m)$,および $n$ から構成されるブロックが有効であるとは,ハッシュ値 $H(p||M(m)||n)$ の先頭 $k$ 文字が 0 となることである. |
注意したいのは,Merkle tree の値 $M(m)$ がコインベーストランザクションのナンス $m$ を入力に持つ関数(の出力)になっていることです.Merkle tree はハッシュポインタで構成される二分木なので,ナンス $m$ を変える(すなわち葉ノードの値を変える)ことによって根ノードの値も変動し,ブロックのハッシュ値が変化します.
マイニング
ところで,コインベーストランザクションとは,新しいコインを作成するトランザクションなのでした.トランザクションの出力を自分に指定しておけば,新しいコインを貰うことができます.「トランザクション編」からずっと説明を怠っていましたが,そろそろコインベーストランザクションを発行して,コインを作成したくなってきました.
コインベーストランザクションを承認されるための唯一の方法は,新しい有効なブロックを提示し,そのブロックが承認される(ブロックチェーンに組み込まれる)ことです(前述の通り,ブロックにはひとつだけコインベーストランザクションが含まれます).そこで,新しいコインを発行したい人々は,新しい有効なブロックを探すことになります.ビットコインにおいて,新しい有効なブロックを探すことや発見すること,あるいはそれによって新たなコインを作成することを マイニング(mining) または 採掘 と言います.マイニングを行うビットコインユーザーは マイナー(miner) または 鉱夫 と呼ばれます.
マイニングで発行できるビットコインの額は,それがビットコインのブロックチェーンでいくつ目のブロックなのかによって決められています.具体的には,最初のブロックの 50BTC からはじまり,210,000 ブロックごとに半分になります.2019年12月20日現在,累計およそ 609,000 ブロックがマイニングされており,発行額は 1ブロックにつき 12.5BTC です1.2140年頃には最小単位2を下回ると言われており,以降のマイニングでは新たにビットコインを発行できなくなります3.初期値の 50BTC や 210,000 ブロックごとに半減することの意図については,筆者が詳しく理解できていないため説明できません.無念です.
Proof of Work
上述の「有効なブロック」(枠線で囲まれた記述)からもわかる通り,有効なブロックを発見することは,ブロックが条件をみたすようなナンスの組 $(n, m)$ を発見することと本質的に同じです.新しいブロックをマイニングしようとする人々は,そのようなナンスの組を求めることになります.
いま,ハッシュ関数 $H$ は秘匿性を持つので,目的のハッシュ値からそれをみたすような入力 $p||M(m)||n$ を求めることは困難です.さらに,$H$ はパズル親和性を持つので,ナンスの組 $(n, m)$ を $2^{256}$ より大幅に小さい時間で計算することも困難です(ビットコインで用いられるハッシュ関数 SHA-256 が出力するハッシュ値は 256-bit です).基本的には,先頭 $k$ 文字が 0 になるハッシュ値が出るまで,ナンスの取り得る値を片っ端から試すことになります.
「解を求めることが困難だが,解の正当性は簡単に検証できる問題」の解を proof of work と言います(文脈により,そうした問題自体を指す場合もあるようです).ナンスについて考えてみると,有効なナンスの組を発見するのは困難ですが,提示されたナンスの組の検証はハッシュ値を計算するだけで行えるため簡単です.したがって,ナンスの組は proof of work であり,ビットコインのマイニングは proof of work を求める問題であると言えます.
マイニングや proof of work についてわかったところで,ビットコインの送金プロセスを再び書き直すと,次のようになります.
| ビットコインの送金(ver.4) |
|---|
| ${\texttt 1.}$ アリスがボブに 1BTC を送金するトランザクションを用意する. ${\texttt 2.}$ アリスがトランザクションに署名し,自分の公開鍵と併せて提示する. ${\texttt 3.}$ マイナーがアリスのトランザクションを含めたブロックを準備する. ${\texttt 4.}$ マイナーがブロックの proof of work を求め,ブロックを提示する. ${\texttt 5.}$ ビットコインの管理者がブロックを検証する. ${\texttt 6.}$ ビットコインの管理者がブロックをブロックチェーンに追加する. |
難易度
以下のように再帰的な定義で決定される値を **難易度(difficulty)**と言います.これは,直前の 2016ブロックをマイニングしていた期間におけるブロック発見効率から決定されるパラメタです.
$$難易度 = 直前の難易度 \cdot (2016 \cdot 10 ~{\rm min})/(直前の~2016ブロックのマイニングに要した時間).$$
2016というのはヒューリスティックな数字です.上記の式は,およそ 10分にひとつ新たなブロックが発見されるように,2016ブロックごとに難易度が再調整されることを意味します.すべてのブロックが 10分おきに発見されるとすれば,2016ブロックのマイニングにはちょうど 2週間かかります.
上に現れた値 $k$(ハッシュ値の先頭に並ぶ 0 の数)は,この難易度から決定されるものです.具体的には,難易度 $d$ に対して $k = \lfloor\log_2{d}\rfloor$ となる値です.人々が熱心にマイニングを行うと,おそらく新しいブロックを発見する間隔は短くなり,$k$ の値が増大して,マイニングは難しくなると予想されます.逆も然りですが,今のところビットコインのマイニングは大局的に見て難化の一途をたどっているようです.
おわりに
今回はビットコインのデータ構造とマイニングの仕組みを紹介しました.この記事の要点は以下の通りです.
- ブロックチェーンは,ブロックと呼ばれるノードをハッシュポインタで繋いだ連結リストである.
- ビットコインはブロックチェーンを用いて,台帳に改竄耐性を与えている.
- ビットコインのマイニングとは,ナンスと呼ばれる proof of work を算出し,新しい有効なブロックを発見することである.
- ビットコインの送金は(現時点での知識では)以下のように行われる.
| ビットコインの送金(ver.4) |
|---|
| ${\texttt 1.}$ アリスがボブに 1BTC を送金するトランザクションを用意する. ${\texttt 2.}$ アリスがトランザクションに署名し,自分の公開鍵と併せて提示する. ${\texttt 3.}$ マイナーがアリスのトランザクションを含めたブロックを準備する. ${\texttt 4.}$ マイナーがブロックの proof of work を求め,ブロックを提示する. ${\texttt 5.}$ ビットコインの管理者がブロックを検証する. ${\texttt 6.}$ ビットコインの管理者がブロックをブロックチェーンに追加する. |
実際には,台帳は分散システムで管理されているため,権限のある特定の個人や団体が管理しているわけではなく,ビットコインの利用者すべてが管理権限を持っています.次回「ネットワーク編」ではこれについて紹介し,いままで説明のために登場させてきた「ビットコインの管理者」とやらを排除したいと思います.
誤字や内容の間違いがありましたらご指摘ください.
お疲れさまでした.
前回:ビットコイン技術入門 1/3(トランザクション編)
次回:ビットコイン技術入門 3/3(ネットワーク編)(いつか書きます)
-
これまでビットコインの単位として,説明なしに「BTC」を用いてきましたが,厳密にはビットコインに「ドル」「円」のような単位はありません.しかし,トランザクションにおいて金額として記述可能な数値の最小単位が,通例 satoshi と呼ばれています(Bitcoin の創始者 Satoshi Nakamoto(中本哲史)に因んだものです).利便性のための別表現として,100,000,000 satoshi が 1BTC(または 1 bitcoin)と呼ばれています. ↩
-
現在のルールが変更されなければ,ビットコインは総額約 2100万BTC が発行されて,そこで打ち止めになります.その後は新しいコインを発行できなくなるため,マイニングのインセンティブは減少します.しかし,この一連の記事では扱っていませんが,ビットコインにはマイニングで得られるの利益として新規コイン以外にも取引手数料というものがあるため,打ち止め後のマイニングでは必ずしも利益がゼロになってしまうというわけでもありません. ↩