[Unity]インタラクティブな水面の表現をやってみる

みなもは しずかに ゆれている
....なみのりを つかいますか？

スィ〜〜〜〜〜〜

概要

グレンジ Advent Calendar 2021 3日目担当の、flankids です。
普段はインプット管理、カメラワーク作り、アニメーション制御などなどで遊び心地を作ることを主にやってるエンジニアをしています。

今回はUnityで

• 光の性質を加味した水面の表現
• 波動方程式を使った波の表現

をやってみました。
もし気に入っていただけたら、LGTM(いいね)やストックをしてもらえるとスゴく嬉しいです！

参考にした記事を先に紹介しておきます！

• モバイルアプリにおけるアーティストフレンドリーな水面表現戦略 - slideshare
• 水面を作ってみた - しゅみぷろ

両方をほとんどそのまま踏襲してマージしたのが今回の表現になります。
ありがたい記事に感謝・・・！

各記事内のコードやサンプルプロジェクトがそのまま参考になるため、本記事ではざっくり概要の解説をします。

光の性質を加味した水面の表現

まずは光の性質を加味して、クオリティ高く見える水面の表現です。
今回は以下の３つのテクニックを使ってビジュアルを作りました。

• キューブマップを使って映り込みを表現
• ノーマルマップを使って水面の凹凸を表現
• フレネル反射という光の性質を再現して水面の透け具合をリアルに表現

キューブマップを使って映り込みを表現

キューブマップとは、周囲の環境のリフレクションを表現する正方形テクスチャが 6 つで一組になったもの。
モデルへの周囲の風景の映り込みなどを表現するために使われることが多いです。

今回は、青空と雲が広がるキューブマップを使って水面に映る空を表現します。

WaterSurface.shader

// 視点からのベクトルと法線から反射方向のベクトルを計算する
half3 reflDir = reflect(-i.toEye, i.normal);
float4 col = texCUBE(_Cube, reflDir);

reflectを使って、視線から頂点へのベクトルを反射させたベクトル計算します。
それを使ってキューブマップをサンプリングすることで、映り込みを反映しています。

反射ベクトルを使ってピクセルシェーダーの色を決めているので、普通にテクスチャを反映するのと違って、角度を変えることで映り込みなりの色の動きがあることが確認できます。

ノーマルマップを使って水面の凹凸を表現

次にノーマルマップを使ってフラットなポリゴンに凹凸を与えます。

WaterSurface.shader

// ノーマルマップから法線情報を取得する
float3 localNormal = UnpackNormalWithScale(tex2D(_BumpMap, i.uvNormal), _BumpScale);
// タンジェントスペースの法線をワールドスペースに変換する
i.normal = i.tangent * localNormal.x + i.binormal * localNormal.y + i.normal * localNormal.z;

tangentやbinormalを使ってモデルの持つ法線にノーマルマップを上乗せする形で計算しています。

これだけで水面っぽい凹凸は生まれるのですが、水流を表すためにノーマルの位置をUVスクロールで動かしてみましょう。

WaterSurface.shader

float2 scroll = float2(_ScrollSpeedX, _ScrollSpeedY) * _Time;

// ノーマルマップから法線情報を取得する
float3 localNormal = UnpackNormalWithScale(tex2D(_BumpMap, i.uvNormal + scroll), _BumpScale);

少しずつ水面っぽくなってきました。

フレネル反射を再現して水面の透け具合をリアルに表現

フレネル反射とは、水面に対して垂直に覗き込むと大部分が透けて見えて、覗き込む角度が平行に近づくほど透明度が減って見えるという水面に見られる現象です。

先に実装結果を出します。

カメラの角度によって水面の透け具合が変化し、視点が水面に対して並行に近づくほど透明度が減り、空の映り込みが強く反映されることがわかると思います。
ノーマルで表現された凹凸の角度もこの現象に影響するため、透明度は視点と法線の角度によって決まります。

フレネル反射を実現する実装は以下のとおりです。

WaterSurface.shader

// 水のF0値（正面から見たときの反射率）は0.02
#define F0 0.02

~~中略~~

// フレネル反射率を反映
half vdotn = dot(i.toEye, i.normal);
half fresnel = F0 + (1 - F0) * pow(1 - vdotn, 5);
col.a = fresnel;

視線から頂点へのベクトルと法線の内積を使って、フレネル反射を反映するためのアルファ値を計算します。
水面に対して垂直に覗き込んだときの透明率（F0値）は定数で0.02＝2%として定義しています。

これでフレネル反射を再現することができました。
ノーマルによる凹凸もあり、透明度がまばらだったり、角度を変えると透明度が変化したりと、かなり現実の水面に近い質感が表現できたと思います！

TIPS: さらなる水面の表現

• モバイルアプリにおけるアーティストフレンドリーな水面表現戦略 - slideshare

ここまでの実装の参考にした上記公演スライドでは、さらに

• 深さに合わせた水中の色
• コースティクス（水面によって屈折した光が水底に投影されてできる独特の模様）

について解説されています。
本記事ではひとまず水面だけを考えた表現に留めているため、興味がある方は是非上記スライドをご覧ください！

波動方程式を使った波の表現

ここまでは水面の質感を表現する工程でした。
インタラクティブな水面にするためには、外からの影響で水面の凹凸が変化する必要があります。

そのために「波動方程式」を使って波の動きをシミュレートします。
波動方程式は水面の波紋以外にも、音波、電磁波などのいろんな振動・波動現象を計算する方程式です。

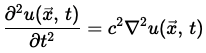波動方程式

波動方程式自体の解説は割愛します。（というか僕もちゃんと分かってません・・・）
下記サイトがパラメータを調整できるデモもついていて分かりやすそうです。
https://ryukau.github.io/filter_notes/waveequation/waveequation.html

上記Githubのプロジェクトで、波動方程式を使って波を作る実装が紹介されていたので、そちらを参考にしました。

1. 同開発者さんによるInkPainterというアセットで、指定した位置のテクスチャを塗り、波発生源の入力として扱う
2. 波の動きのシミュレートする Wave.shader に波発生源の入力を渡す
3. Wave.shader でシミュレートの結果を赤色で表現されるハイトマップとして出力
4. ハイトマップを法線として反映

という流れで、ここまでで作った水面に波の動きを追加しています。

Wave.shader

float2 stride = float2(_Stride, _Stride) * _PrevTex_TexelSize.xy;
half4 prev = (tex2D(_PrevTex, i.uv) * 2) - 1;
half value =
    (prev.r * 2 -
        (tex2D(_Prev2Tex, i.uv).r * 2 - 1) + (
        (tex2D(_PrevTex, half2(i.uv.x+stride.x, i.uv.y)).r * 2 - 1) +
        (tex2D(_PrevTex, half2(i.uv.x-stride.x, i.uv.y)).r * 2 - 1) +
        (tex2D(_PrevTex, half2(i.uv.x, i.uv.y+stride.y)).r * 2 - 1) +
        (tex2D(_PrevTex, half2(i.uv.x, i.uv.y-stride.y)).r * 2 - 1) -
        prev.r * 4) *
    _C);
float4 input = tex2D(_InputTex, i.uv);
value += input.r;
value *= _Attenuation;
value = (value + 1) * 0.5;
value += _RoundAdjuster * 0.01;
return fixed4(value, 0, 0, 1);

WaterSurface.shader

//波動方程式の解を_WaveTexで受け取り、波による歪み具合を法線に反映
//_WaveTexは波の高さなので、高さの変化量から法線を求める
float2 shiftX = { _WaveTex_TexelSize.x,  0 };
float2 shiftZ = { 0, _WaveTex_TexelSize.y };
shiftX *= _ParallaxScale * _NormalScaleFactor;
shiftZ *= _ParallaxScale * _NormalScaleFactor;
float3 texX = 2 * tex2Dlod(_WaveTex, float4(i.uvNormal.xy + shiftX,0,0)) - 1;
float3 texx = 2 * tex2Dlod(_WaveTex, float4(i.uvNormal.xy - shiftX,0,0)) - 1;
float3 texZ = 2 * tex2Dlod(_WaveTex, float4(i.uvNormal.xy + shiftZ,0,0)) - 1;
float3 texz = 2 * tex2Dlod(_WaveTex, float4(i.uvNormal.xy - shiftZ,0,0)) - 1;
float3 du = { 1, 0, _NormalScaleFactor * (texX.x - texx.x) };
float3 dv = { 0, 1, _NormalScaleFactor * (texZ.x - texz.x) };
float3 waveNormal = normalize(cross(du, dv));
i.normal = i.tangent * waveNormal.x + i.binormal * waveNormal.y + i.normal * waveNormal.z;

これで外からの影響で波が発生する水面が作れました！

波を発生させる方法

今回、波の動きのシミュレーションの参考先にした記事を踏襲して、記事の著者が開発した InkPainter というアセットを使って波の発生位置を指定しています。
InkPainterとは、Unityでテクスチャペイントを行えるようになるアセットです。
波の発生位置を表すテクスチャを塗り、波動方程式を行うシェーダーの入力テクスチャとして扱っています。

クリック位置が波の発生位置となるように実装しましたが、応用すればキャラクターの足に判定を仕込み、歩く動きに合わせて波を発生させることもできます。

まとめ

• 光の性質を加味した水面の表現
• 波動方程式を使った波の表現

を使ってインタラクティブな水面の表現をやってみました。
どちらも現実世界の物理現象を再現する内容で、リアルな表現には物理や科学、気象などについて向き合わないといけないことが多いなと改めて感じました…引き続き精進します！

来週と再来週の金曜日も同じアドベントカレンダーに記事を投稿する予定です。
もしよろしければ、引き続き読んでいただけると嬉しいです。