スリザーリンクと論理回路と将来と。

この記事は、
ペンパアドベントカレンダーhttps://adventar.org/calendars/3414
の第10日目の企画です。

皆様、初めまして。fffと申します。スリザーリンク狂です。

さて、皆様はスリザーリンクというパズルをご存じでしょうか？
スリザーリンクのルールはこちらから確認できますので、ルールが心配な方はご確認ください。
https://www.nikoli.co.jp/ja/puzzles/slitherlink/
以下スリザーリンクのルールと初級手筋がわかっていることを前提とします。

今まで、スリザーリンクと情報分野ではいくつかの研究/開発がされてきました。
例えばスリザーリンクのソルバーはいくつかネットで公開されているものがありますし、スリザーリンクを解く行為のNP完全性は以下に挙げる論文で示されています。
http://www-imai.is.s.u-tokyo.ac.jp/~yato/data2/SIGAL74-3.pdf

そして今回、スリザーリンクそのものの演算能力等について考えてみました。
まず、共通解/入出力を以下のように定義し直します。

######共通解の定義
以下、スリザーリンクの「共通解」とは、複数存在するスリザーリンクの解答盤面の全てにおいて共通してひかれる線のことを指す。

どうしても唯一解問題にするのがきつかったのでこの定義を導入しました。
######入出力の定義
入力　回路全体では各ビット(0,1)に対応したヒントを定義し、入力部にそのヒントを配置すること、各素子では特定の部分に線が引かれることを1、引かれないことを0とする
出力　共通解の特定の部分に線が引かれることを1、引かれないことを0とする。

入出力といってもいじれるのはヒント数字と解しかありませんしこれもある意味妥当とは思います。

定義はこれくらいにして、これからスリザーリンクで論理値を扱う方法について解説していきます。
###スリザーリンク回路　初級編
まず、この後の論理回路を組む上でいくつか必要になる論理回路をスリザーリンクで実装していきます。
####not回路
notは、入力が1の時に0を出力し、入力が0の時に1を出力するものです。
これは次のようなスリザーリンクの機構によって実現可能です。
http://pzv.jp/p.html?slither/10/10/zs00ajax03bzr

実際に成立しているか試してみましょう。
まず、入力が1(線が通る)の時は次のようになり、確かに出力は0(線が通らない)です。

逆に、入力が0(線が通らない)の時には次のようになり、確かに出力は1です。

このとき、出力部以外にループの端点(下方向に伸びているやつ)が生じていますね。この端点を後で処理するので忘れないようにしておきましょう。

####xor回路
xorは、入力を二つ受けとり、入力が二つとも同じ時0を、違う時に1を出力する回路です。二進数の足し算をした時の一桁目に対応している、と言った方がわかりやすい人もいるかもしれません。
xor回路は次のようにして実現可能です。
http://pzv.jp/p.html?slither/10/10/zs00atao0akazj

いくつか試してみましょう。入力が00の時、出力は0です。

次に、入力が10の時、出力は1です。

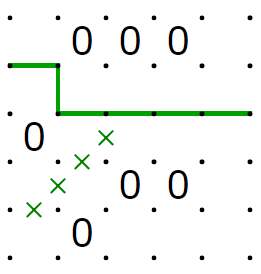
次に、入力が11の時、出力は0です。

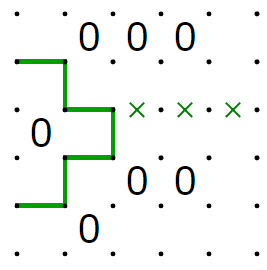
入力が01の時は割愛しますが、この場合も成立しています。

####and回路
and回路は、二つの入力がどちらも1の時に1を出力し、そうでないときは0を出力する回路です。
この回路は次のようにして実現可能です。
http://pzv.jp/p.html?slither/10/10/s000ahandk5603bidlazv

試してみましょう。まず、入力がどちらも1のときの出力は1です。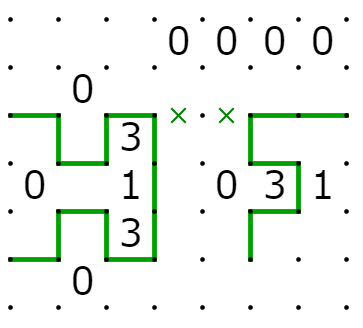
次に、入力が10あるいは01の時、出力は0です。


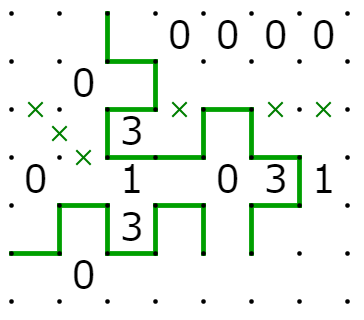
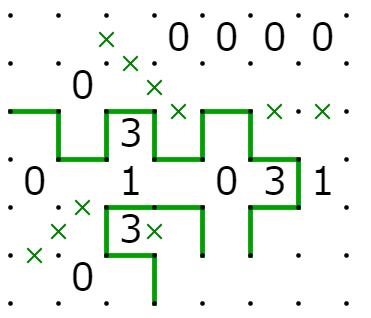
最後に、入力が00の時、出力は0です。

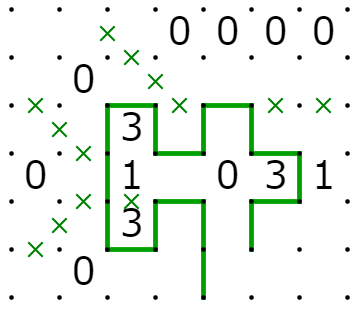
####分岐
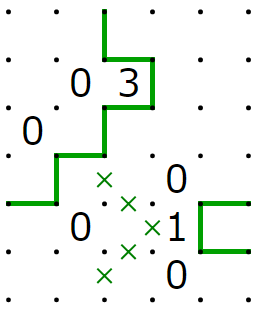
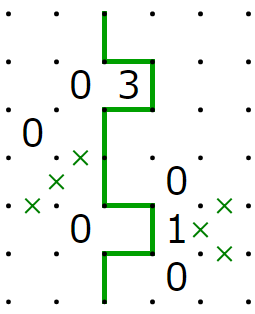
電子回路では容易に作れるがスリザーリンクでは作りにくいものとして分岐があります。これは、入力が1の時は1を二つ出力し、入力が0の時は0を二つ出力するものです。これは、次のようにして実現できます。
http://pzv.jp/p.html?slither/10/10/r0dkapak5bmazzi

確かめてみましょう。まず、入力が1の時は出力はともに1です。

また、入力が0の時は出力はともに0です。

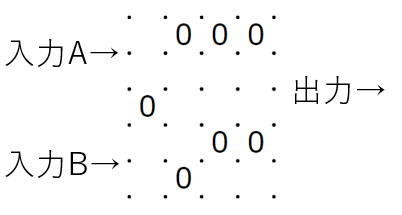
####交差
同じく電子回路では容易だがスリザーリンクでは作りにくいものとして交差があります。記号で書けば下に書いたものです。

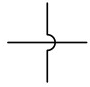
これを通常の盤面で実現する方法を思いつきませんでした。しかし、切り貼りを認めた特殊盤面ならば可能です。

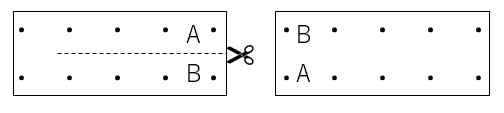
上の図のように盤面の一部を切って、同じアルファベットが重なるように貼りなおせばたしかに交差が実現できています。

####解の存在
ここまでいくつかの回路を紹介してきましたが、各回路では入力でも出力でもない端点がいくつもありました。しかしこれらはあくまでスリザーリンクなので、少なくとも一つ解が存在しなければなりません。
そこで、すぐ上の交差のところで使った切り貼りを利用します。
具体的には、
1.十分にひろい盤面（解生成盤面と呼びます）を、回路の盤面とはべつに用意する。
2.各回路の、入出力に関係ない端点を生じうるすべての点から、切り貼りによって解生成盤面に一列につなげる
ことで解が生じるようになります。

###半加算器を作ってみた
文字で見てもよくわからないことが多いかと思いますので、ここでは半加算器を作ってみようと思います。半加算器は、二進数の足し算を行う装置です。

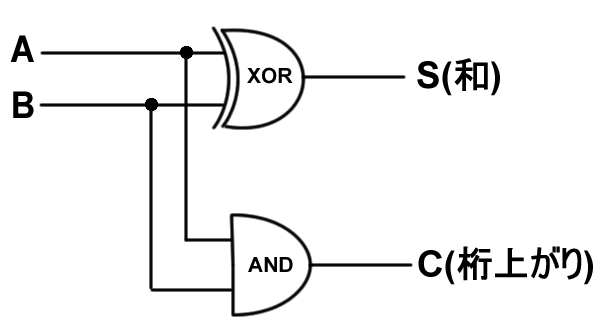
（甲南大学の資料より、http://kccn.konan-u.ac.jp/information/cs/cyber08/cy8_cmex.htm）
この図を見てもらえばわかる通り、今までに説明したxor、and、分岐、交差を使った回路なので作ることが可能です。
実際に作ってみました。

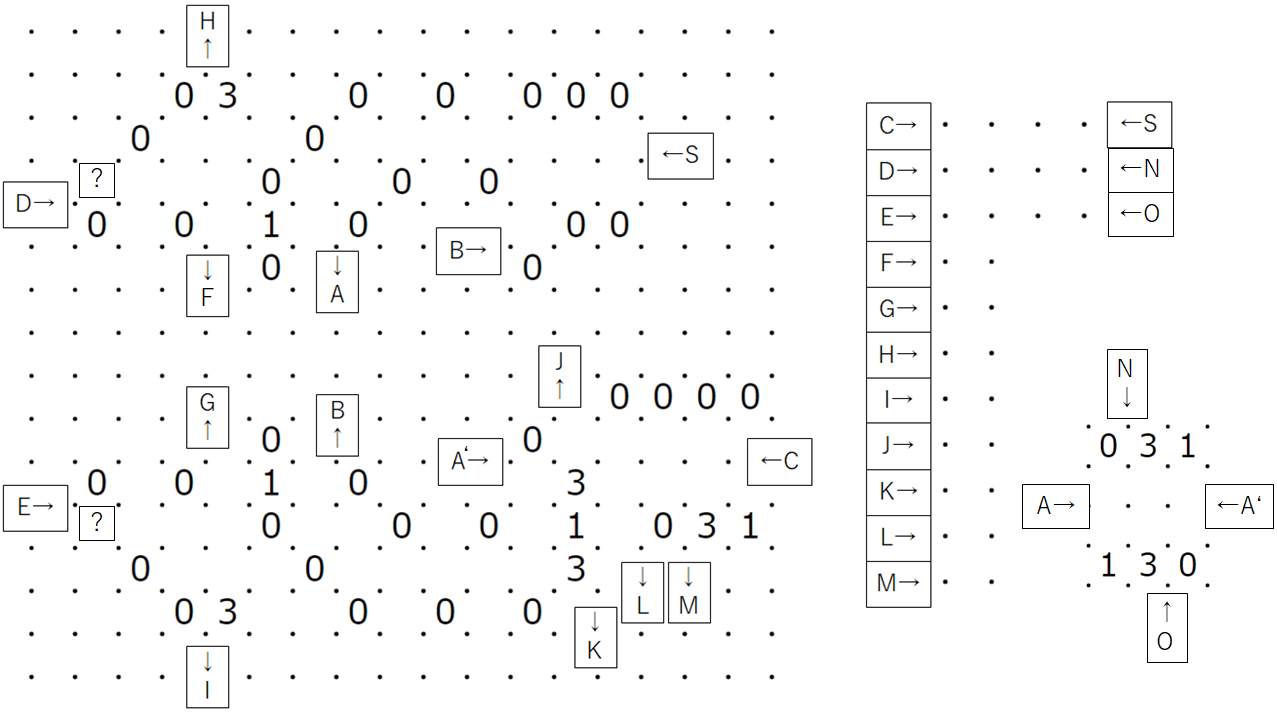
右についている回路はそれぞれ、解を存在させるため、小さなループが発生することを避けるためです。
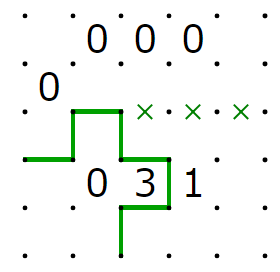
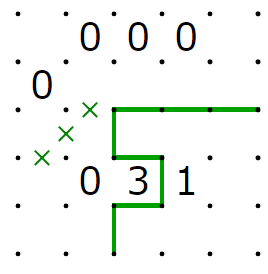
上のスリザーリンクでは、同じアルファベットが書かれたところがつながっている、と考えてください。この？は、回路全体の入力に対応しています。入力が0の時？には0が、入力が1の時には3が入ります。
出力は2進数表記で1の位はS,2の位はCに対応しています。
何が起きているのかよくわからないかもしれませんが、試しに1+1を計算してみましょう。

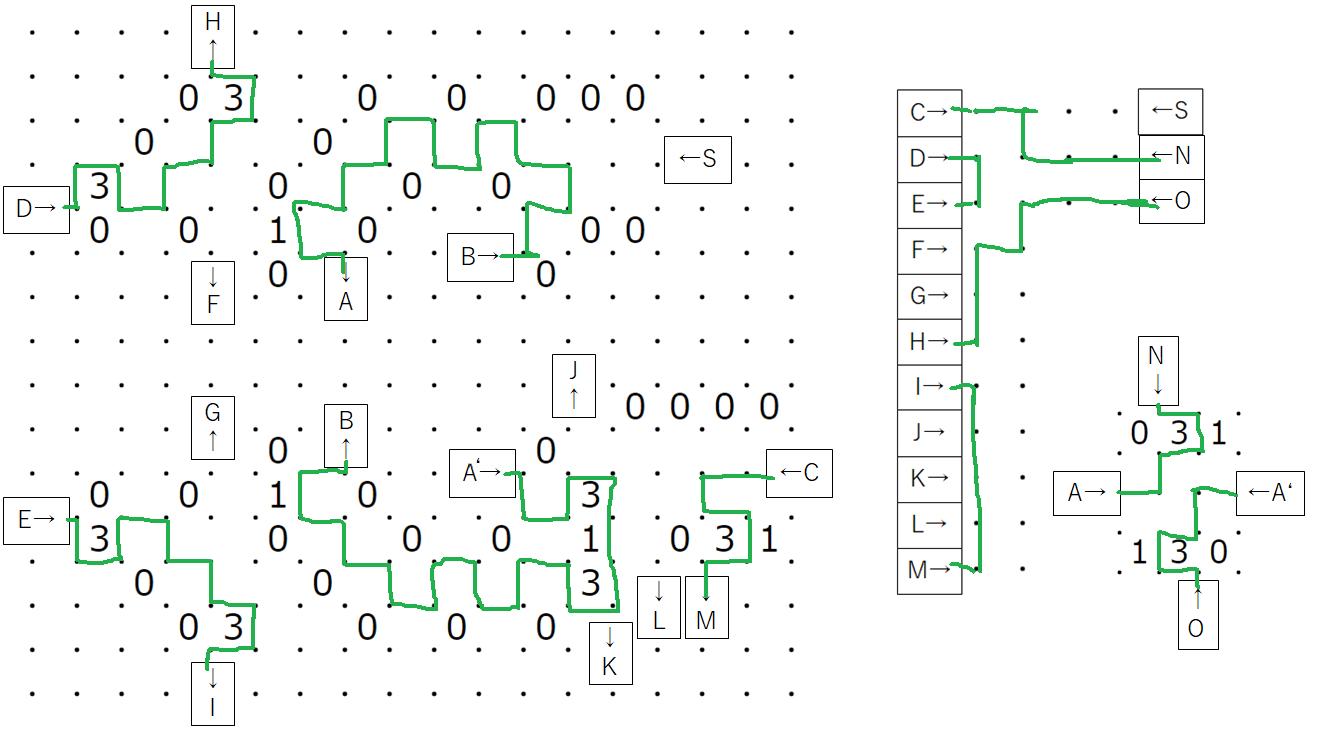
上に上げたのは二つの？に3を代入して解いた時の解のうちの一つです。たしかにC=1、S=0となっていて、1+1＝10(2進法表記)=2(10 進法表記)となることがわかります。
？にほかの数字をいれてみても、足し算が成立することは簡単に確かめられます。

しかし、スリザーリンクの力をもってすれば、単純に半加算機とおなじ出力を得るだけならばより簡潔にすることができます。
実は、ここまであえて回りくどい方法をとったのは、論理回路をスリザーリンクで置き換える、ということが可能であることをを導入するためでした。

次の目標は
###特定の条件下の任意のスリザーリンクを解ける機械はチューリング完全である。
ことを示すことです。
(示したつもりですが、専門分野ではないため誤りがある可能性があります。もし誤りを見つけた方がいらっしゃいましたらfffpuzzle(アット)gmail.comまでご連絡いただけると幸いです)
細かいことをいうと、以下で述べるスリザーリンクを解くと、入出力がルール110セルオートマトンというチューリング完全のものを模倣しているため、スリザーリンクをとける⇒ルール110セルオートマトンを再現できる⇒その機械はチューリング完全、ということです。
ただし、この記事はあくまで「ペンパ」アドベントカレンダーですので、概要のみを解説することにします。（行間広めです）

######チューリング完全とは？
チューリング完全というのは、ざっくり言うと計算能力がある基準を満たしていることを保証するものです。例えば多くのプログラミング言語はチューリング完全であることが知られています。

######ルール110セルオートマトンとは？
無限に長いテープに、1または0が一列に書き込まれているとします。このときに、次の操作を全ての数字にたいし同時に行って数字を書き換えることで新しい数字列を作ることをします。
・ある数字とその前後の数字が
000，111，100の時0に、
それ以外の時1に書き換える

######基本の考え方
半加算器の時に示した通り、論理回路はスリザーリンクで置き換えることができました。
今、not,xor,andを再現できていますが、この3つを再現できればその組み合わせでどのような論理演算(入出力の組み合わせ)も再現できることが知られています。
したがって、3つの入力を受け取り、ルール110セルオートマトンの出力と一致するような論理回路を作り、スリザーリンクで置き換えることができます。
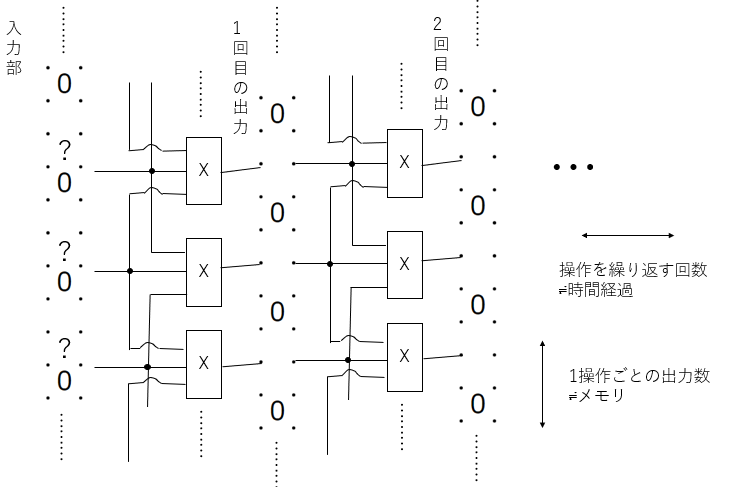
あとは、下図の回路のようにスリザーリンクを作れば、スリザーリンクの共通解がルール110セルオートマトンの出力と一致します。

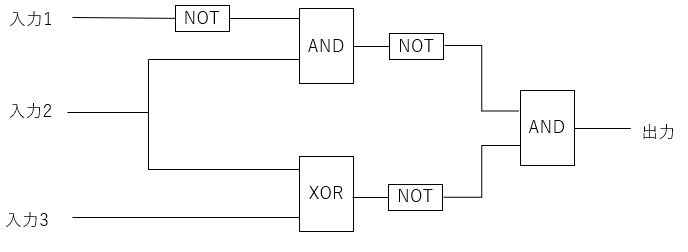
この回路の方針を簡単に説明すると、入力2、3の値が一致している、かつ011でないものについて1を出力するようになっています。
この回路のことを省略してXと書くことにすると、下のスリザーリンクはルール110オートマトンにおけるルールに従って数列を操作したときの結果を見ることができるようになっているとわかります。

特に、上下、左右の幅を有限にとどめたものはスリザーリンクのルールに則って共通解を得ることが可能です。
従ってこの論理回路に対応したスリザーリンクを解くことができる機械はルール110セルオートマトンの出力を再現できることになり、チューリング完全であることがいえます。

####スリザーリンクの将来
最後に、(本来のアドベントカレンダーの目的であった)スリザーリンクの魅力や今後についてを語ろうとおもいます。
私は、スリザーリンクの良さは小規模手筋と大規模な手筋のバランスにあると思います。
スリザーリンクのヒント数字は基本的にはせいぜいその数字を含むマスと、そのマスに隣接するマスまでしか影響しません。しかし、「全体が一つの大きなループになる」という制約のおかげで盤面全体に個々のヒントが影響してくるようなパズルが作れるようになるのです。
そして、全体を見てその制約に気づいたときに一気に線が引ける、というのもループ系ならではの強みだと思います。
現状、スリザーリンクは単純で小規模な手筋の多くが発見/研究されており、その見せ方や、まだ未開発の中～大規模な手筋を研究していくことが今後の課題とされています。
私は、スリザーリンクは盤面全体を見る必要のあるような、いわば一発ネタ的な大規模手筋がまだまだ多く残されているように感じますし、そこを研究することが上で上げたようなスリザーリンクの良さを最も生かせそうなのです。
そして、新しい一発ネタの発想は、「スリザーリンク」という枠組みの中で考えていても思いつけないようなものもあるかもしれません。例えばこの記事で述べたような、スリザーリンクと論理式の関係を考える、という試みはその一つです。
過去にはスリザーリンクと電車のポイント切り替えについて考えながら年賀パズルを試行錯誤して作っていて、次のようなスリザーリンクを思いつきました。(fffのパズル日記/2016年1月の記事より)
http://pzv.jp/p.html?slither/11/11/ahchaicl1333biaaahbcch233211chdbdhbabi0323albiahcha
スリザーリンクと○○、スリザーリンクと△△……。いろいろな組み合わせをイメージしながら数字を調整してみる。それだけでも、ひょっとするとスリザーリンクの枠を打ち破り
新しい世界を見ることができるかもしれないな、と思っています。

最後までお付き合いいただきありがとうございました。
著　fff
協力　gotoloop