Salome-Meca2019による軸対称圧力容器の解析結果と公式の比較

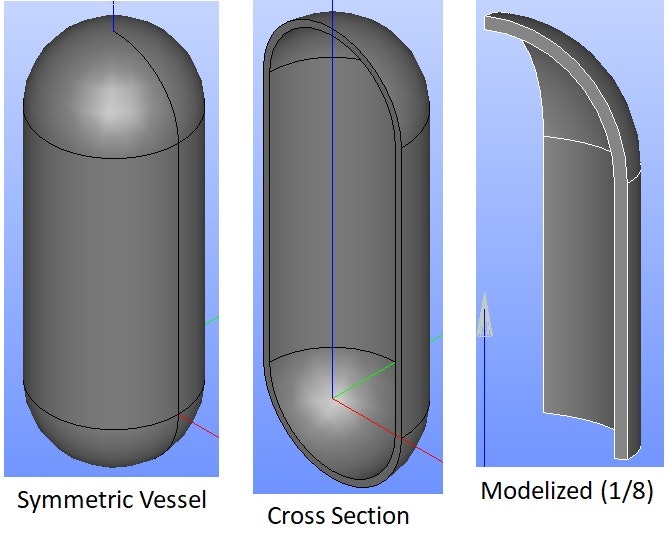
解析対象の概要

公式に基づく設計が規格化されている圧力容器について，公式と解析による応力分布の対応を検討してみる

※ Salome-Meca2015による解析手順を記載した以下に従い,Salome-Meca2019に焼き直した
(https://www.slideshare.net/stebee19/ax-symmetricpressurevesselelasticstressanalysis)

• 材料特性

ヤング率 E = 200 GPa
ポアソン比 ν = 0.3

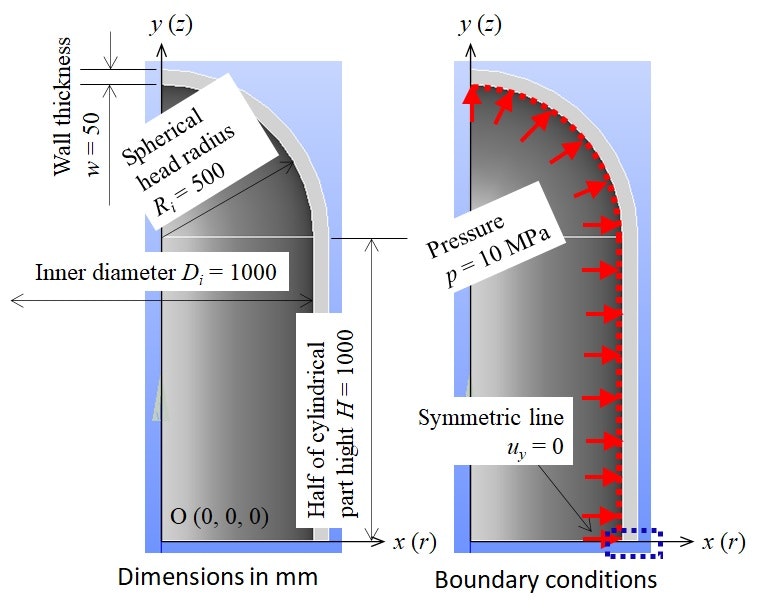
• 容器の形状・寸法と境界条件

内径 D_in = 1000 mm
円筒胴部長さ L = 2000 mm
肉厚 w = 10 mm
内圧 p = 10 MPa
とすると，設計公式（平均径公式 = mean-diameter hoop stress formulae）から得られる周方向応力（最大主応力）σ_θ = pD/w = 105 MPa
※ D は板厚中心を基準とする平均外径
つり合い関係から求められる周方向応力 σ_θ = pD_in/w = 100 MPa

#モデル化

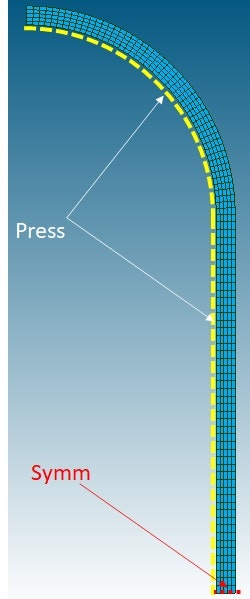
• 主に軸対称六面体ソリッド要素となるよう規則的に要素分割し，二次要素化する．子午線および胴長手方向に50均等分割，板厚方向に5均等分割

• グループ定義
  内圧を受ける線にEdgeグループ Press，上下対称線にSymmを定義

#結果
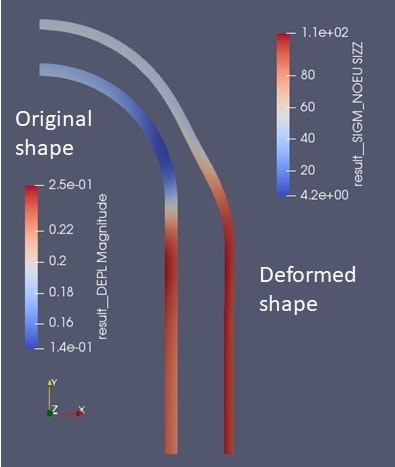
変形図と周方向応力のコンター図

mesh = LIRE_MAILLAGE(FORMAT='MED',
                     UNITE=2)

model = AFFE_MODELE(AFFE=_F(MODELISATION=('AXIS', ),
                            PHENOMENE='MECANIQUE',
                            TOUT='OUI'),
                    MAILLAGE=mesh)

mater = DEFI_MATERIAU(ELAS=_F(E=200000.0,
                              NU=0.3))

materfl = AFFE_MATERIAU(AFFE=_F(MATER=(mater, ),
                                TOUT='OUI'),
                        MODELE=model)

mecabc = AFFE_CHAR_MECA(DDL_IMPO=_F(DY=0.0,
                                    GROUP_MA=('Symm', )),
                        MODELE=model)

mecach = AFFE_CHAR_MECA(MODELE=model,
                        PRES_REP=_F(GROUP_MA=('Press', ),
                                    PRES=10.0))

result = MECA_STATIQUE(CHAM_MATER=materfl,
                       EXCIT=(_F(CHARGE=mecabc),
                              _F(CHARGE=mecach)),
                       MODELE=model)

result = CALC_CHAMP(reuse=result,
                    CONTRAINTE=('SIGM_ELNO', 'SIGM_NOEU'),
                    CRITERES=('SIEQ_ELNO', 'SIEQ_NOEU'),
                    FORCE=('REAC_NODA', ),
                    RESULTAT=result)

IMPR_RESU(FORMAT='MED',
          RESU=_F(NOM_CHAM=('DEPL', 'REAC_NODA', 'SIGM_ELNO', 'SIGM_NOEU', 'SIEQ_ELNO', 'SIEQ_NOEU'),
                  RESULTAT=result),
          UNITE=3)

IMPR_RESU(FORMAT='RESULTAT',
          RESU=_F(GROUP_MA=('Symm', ),
                  IMPR_COOR='OUI',
                  NOM_CHAM=('DEPL', 'REAC_NODA', 'SIGM_NOEU', 'SIGM_ELNO', 'SIEQ_NOEU', 'SIEQ_ELNO'),
                  RESULTAT=result),
          UNITE=80)

FIN()

評価

• 数値解
  長手方向中央対称面上の応力分布（IMPR_RESU, FORMAT='RESULTAT'で指定したファイルにテキスト出力してある）
  

• テキスト（*.RESU）をスプレッドシートで開いて後処理を行う

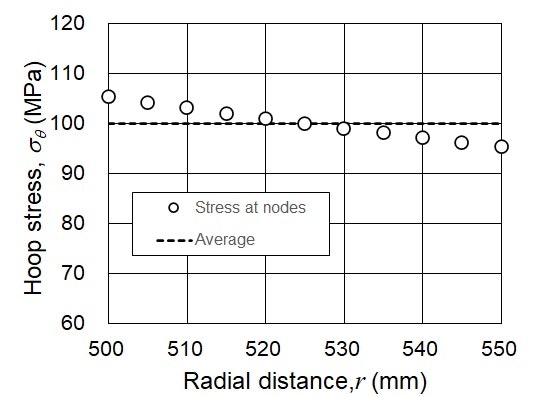
周方向応力の板厚平均をとると（台形公式を使用），100.00116 MPaとなり，つり合い関係から求められる教科書の公式と一致する．周方向応力の板厚方向応力をグラフにすると，内面がやや高めになり，カラーコンター図や点の最大応力に着目すると（安全側ではあるが），公式よりも厳しめの応力評価となる．
　本研究の一部は科学研究費補助金（18K02963，代表：藤岡照高）の助成を受けて実施した．