Salome-Meca2019による片持ちはりの曲げ解析（ビーム要素）

解析対象

• 矩形断面はり

全長 L = 300 mm
幅 b = 100 mm
高さ h = 20 mm

• 境界条件

先端面に集中荷重 P = 1000 N
荷重点の反対側を固定（3方向変位と3軸回りの回転の合計6自由度）

#はりの弾性理論解

• 材料特性
  ヤング率 E = 200 GPa
  ポアソン比 ν = 0.3

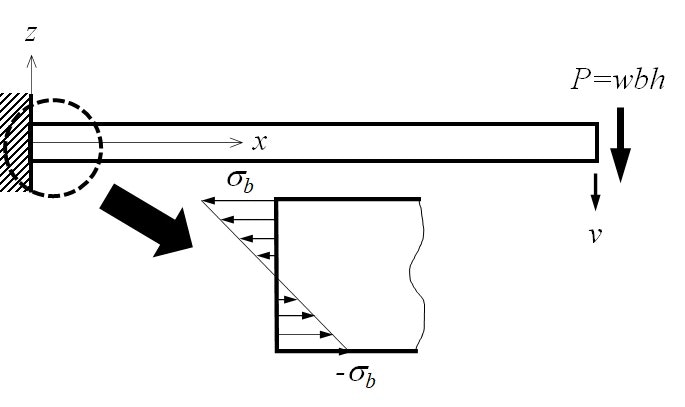
• モデル化と理論解

下図のようにモデル化し，z軸方向の直線が，曲げモーメントを与えた後にも直線を保つと仮定する（Bernoulli-Euler theory）と，自由端変位 v は以下のようになる．

断面二次モーメント I = bh³/12 = 6.6667×10⁴ mm⁴
自由端たわみ v = PL³/(3 EI) = 0.67500 mm
固定端反モーメント M_max = PL = 3.0×10⁵ N・mm
曲げ応力 σ_b = (M_max/I) ×(h/2) = 45.000 MPa

※ 曲げ応力（bending stress）とは，はりの断面での応力の分布が線形と仮定し，曲げモーメントとつり合うようにしたものであり，実際の表面応力とは限らない．

#メッシュ

• チモシェンコはり要素（POU_D_T）
• AFFE_CARA_ELEM で断面形状 RECTANGLE（矩形）と幅 HY = 100，高さ HZ = 20 の寸法を与える
• グループ
  はりの全体：Edgeグループ（Beam）
  左端（固定端）：Nodeグループ（fix）
  右端（自由端，荷重点）：Nodeグループ（load）
• 長さ方向均等15分割

コマンドファイル

コマンドファイルは以下の通り．

mesh = LIRE_MAILLAGE(FORMAT='MED',
                     UNITE=20)

model = AFFE_MODELE(AFFE=_F(MODELISATION=('POU_D_T', ),
                            PHENOMENE='MECANIQUE',
                            TOUT='OUI'),
                    MAILLAGE=mesh)

elemprop = AFFE_CARA_ELEM(MODELE=model,
                          POUTRE=_F(CARA=('HY', 'HZ'),
                                    GROUP_MA=('Beam', ),
                                    SECTION='RECTANGLE',
                                    VALE=(100.0, 20.0)))

mater = DEFI_MATERIAU(ELAS=_F(E=200000.0,
                              NU=0.3))

fieldmat = AFFE_MATERIAU(AFFE=_F(MATER=(mater, ),
                                 TOUT='OUI'),
                         MODELE=model)

fix = AFFE_CHAR_MECA(DDL_IMPO=_F(DRX=0.0,
                                 DRY=0.0,
                                 DRZ=0.0,
                                 DX=0.0,
                                 DY=0.0,
                                 DZ=0.0,
                                 GROUP_NO=('fix', )),
                     MODELE=model)

load = AFFE_CHAR_MECA(FORCE_NODALE=_F(FZ=-1000.0,
                                      GROUP_NO=('load', )),
                      MODELE=model)

reslin = MECA_STATIQUE(CARA_ELEM=elemprop,
                       CHAM_MATER=fieldmat,
                       EXCIT=(_F(CHARGE=fix),
                              _F(CHARGE=load)),
                       MODELE=model)

reslin = CALC_CHAMP(reuse=reslin,
                    CONTRAINTE=('SIEF_ELNO', 'SIPO_ELNO', 'EFGE_NOEU', 'SIPO_NOEU'),
                    FORCE=('REAC_NODA', ),
                    RESULTAT=reslin)

IMPR_RESU(FORMAT='MED',
          RESU=_F(MAILLAGE=mesh,
                  NOM_CHAM=('DEPL', 'EFGE_NOEU', 'SIPO_NOEU', 'REAC_NODA'),
                  RESULTAT=reslin),
          UNITE=80)

IMPR_RESU(FORMAT='RESULTAT',
          RESU=(_F(GROUP_NO=('load', ),
                   IMPR_COOR='OUI',
                   NOM_CHAM=('DEPL', ),
                   RESULTAT=reslin),
                _F(GROUP_NO=('fix', ),
                   IMPR_COOR='OUI',
                   NOM_CHAM=('EFGE_NOEU', 'SIPO_NOEU', 'REAC_NODA'),
                   RESULTAT=reslin)),
          UNITE=2)

FIN()

結果

• 固定端（fix）のテキスト出力（IMPR_RESU FORMAT='RESULTAT'）から
  z方向変位DEPL DZ = 0.67734 mm（理論解 0.6750 mm）
  曲げ応力 SIPO_NOEU SMFY = 45.0000 MPa（理論解 45.0 MPa）

本研究の一部は科学研究費補助金（18K02963，代表：藤岡照高）の助成を受けて実施した．