(こっそりと)アニーリングに関する記事を何本か投稿してきたので、アドベントカレンダーにも思い切って参加することにしました。ところが、面白みのあるネタが思い浮かびません。苦し紛れに、アニーリングのモデル化における「次数下げ」というネタを持ち出してみました。初心者の戯言にお付き合いいただければ幸いです。
そもそも何の話をしようとしているのか
アニーリングマシンに問題を解かせるためには、イジングモデルあるいはQUBOで定式化する必要があります。以降、QUBOを前提に話を進めることにします。QUBOは以下の数式で表現されます。
H(\vec{q}; Q)
= \sum _{i\leq j} Q_{ij}q_{i}q_{j}, \quad \vec{q} = \left(
\begin{matrix}
q_{0} \\
q_{1} \\
\vdots \\
q_{N-1}
\end{matrix}
\right) \in \{ 0, 1 \} ^{N}, \quad Q = \left( Q_{ij} \right) _{1\leq i, j \leq N}.
上記数式からも分かるように、QUBOは2次式で表現されます。アニーリングマシンの入力はQUBO(あるいはイジングモデル)でなければならないため、3次以上の多項式で表現される問題はそのままアニーリングマシンに投入できません。そこで、3次以上の項の次数を下げて、何とか2次式で表現できないか考えてみます。結論だけで十分だよ、という方は結論をお読みください。
制約条件を用いた次数下げの手法
まずは、どのようなアイディアで次数下げを行うのかについて説明します。
具体的な数式から制約条件を導出する
具体的に、$N=3$のケースを例にして考えてみましょう。一番シンプルな3次式を考えると、
H(\vec{q}) = q_{0}q_{1}q_{2}, \quad \vec{q} = \left(
\begin{matrix}
q_{0} \\
q_{1} \\
q_{2}
\end{matrix}
\right)
です。これを2次式に変換するにはどうすればよいのでしょうか。まずは無理やり2次式で表現してみます。つまり、以下のように書いてみます。
H(\vec{q}; y_{0}) = y_{0} q_{2}, \quad y_{0} \equiv q_{0}q_{1}, \quad y_{0} \in \{ 0, 1 \}.
唐突に現れた$y_{0}$は、新規追加したQUBO変数です。QUBO変数を追加したことで数式自体は2次式になっていますが、このままでは何も解決していません。$y_{0} = q_{0}q_{1}$を満たすことを要求しているにも関わらず、上記数式で表したモデルにはその制約条件が反映されていないからです。
制約条件という言葉が出てきました。最適化問題をモデル化する際には、様々な制約条件をモデルに取り込む工夫をしますが、それと似たようなことをします。具体的に言うと、$y_{0} = q_{0}q_{1}$という制約条件が満たされる場合にのみQUBO(つまり$H$)が最小値を取るような項を追加します。この制約条件項は、上記ケースでは$q_{0}, q_{1}, y_{0}$に依存するでしょう。制約条件項を$H_{c}(q_{0}, q_{1}, y_{0})$と書くことにすると、
H(\vec{q}) = q_{0}q_{1}q_{2}
\longrightarrow
H(\vec{q}; y_{0}) = y_{0}q_{2} + \lambda H_{c}(q_{0}, q_{1}, y_{0})
となります。ただし、$\lambda > 0$です。
さて、具体的に$H_{c}$を決める必要があります。大前提として、$H_{c}$はQUBO変数の2次までの多項式である必要があります。ただし、定数項には任意性があるので予め$0$としておきます。
先に、$q_{0}, q_{1}, y_{0}$の関係性を一覧にしてみましょう。下表を参照してください。一番右の列のOKまたはNGは、パターンとして正しいかどうか、つまり$q_{0}q_{1} = y_{0}$を満たしているかどうかを示しています。
| $q_{0}$ | $q_{1}$ | $q_{0}q_{1}$ | $y_{0}$ | |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | OK |
| 1 | 1 | 1 | 0 | NG |
| 1 | 0 | 0 | 1 | NG |
| 1 | 0 | 0 | 0 | OK |
| 0 | 1 | 0 | 1 | NG |
| 0 | 1 | 0 | 0 | OK |
| 0 | 0 | 0 | 1 | NG |
| 0 | 0 | 0 | 0 | OK |
OKになっているパターンについては$H_{c} = 0$、NGになっているパターンについては$H_{c} > 0$となるように制約条件項を定義できれば良さそうです。$q_{0}$と$q_{1}$の入れ替えについて対称であることを考慮すると、
H_{c}(q_{0}, q_{1}, y_{0}) \equiv a q_{0}q_{1} + b(q_{0} + q_{1})y_{0} + c(q_{0} + q_{1}) + d y_{0}
と書けます。上記パターンを代入して、以下を満たすようにパラメータ$a, b, c,d$を決めます。
\begin{align}
H_{c}(1,1,1) &= a + 2b + 2c + d = 0,\\
H_{c}(1,1,0) &= a + 2c > 0, \\
H_{c}(1,0,1) &= b + c + d > 0,\\
H_{c}(1,0,0) &= c = 0,\\
H_{c}(0,1,1) &= b + c + d > 0,\\
H_{c}(0,1,0) &= c = 0, \\
H_{c}(0,0,1) &= d > 0,\\
H_{c}(0,0,0) &= 0. \\
\end{align}
$c=0$がただちに決まるので、
\begin{align}
a + 2b + d &= 0 \\
a &> 0 \\
b + d &> 0
\end{align}
となります。さらに、$a=1, b+d=1$を仮定すると1、$b=-2, d=3$を得ます。以上の結果から、制約条件付きQUBOは以下のように書けます。
H(\vec{q}) = q_{0}q_{1}q_{2} \longrightarrow
H(\vec{q}; y_{0}) = y_{0}q_{2}
+ \lambda H_{c} (q_{0}, q_{1}, y_{0}).
ただし、
H_{c}(x,y,z) \equiv xy - 2(x+y) z + 3z
です。制約条件項$H_{c}$は、この後も使用します。
制約条件を適用する
$N=3$の場合には、QUBO変数1つと制約条件項$H_{c}$を追加することで、2次式に落とし込むことができました。それでは、次数が4以上の項を2次式に変換するためにはどうすればよいのでしょうか。
N=4の場合
$N=4$の場合を考えます。まずは$N=3$の場合と同様に、$q_{0}$と$q_{1}$の積を新しく追加したQUBO変数$y_{0}$に置き換え、
H(\vec{q}; y_{0}) = q_{0}q_{1}q_{2}q_{3} = y_{0} q_{2} q_{3}, \quad y_{0} \equiv q_{0}q_{1}
とします。このとき、制約条件項を付け加えると、
H(\vec{q}; y_{0}) \longrightarrow y_{0}q_{2}q_{3} + \lambda H_{c} (q_{0}, q_{1}, y_{0})
と書けます。4次式から3次式になりました。同じ要領で、さらに新しくQUBO変数$y_{1}$を追加して、制約条件項を追加すれば2次式に変換できます。すなわち、最終的なQUBOは以下のように書けます。
H(\vec{q}; \vec{y}) \longrightarrow y_{1}q_{3} + \lambda \left[ H_{c} (q_{0}, q_{1}, y_{0}) + H_{c} (y_{0}, q_{2}, y_{1}) \right], \quad \vec{y} \in \{ 0, 1\} ^{2}.
N=5の場合
$N=5$の場合を考えてみます。$N=3,4$の例に倣って、QUBO変数の積の左から順に、新しく追加したQUBO変数で置き換えていきます。制約条件を追加していく過程は、以下のようになります。
\begin{align}
H(\vec{q}) &= q_{0}q_{1}q_{2}q_{3}q_{4} \\
&\longrightarrow y_{0} q_{2} q_{3} q_{4} + \lambda H_{c} (q_{0}, q_{1}, y_{0}) \\
&\longrightarrow y_{1} q_{3} q_{4} + \lambda \left[ H_{c} (q_{0}, q_{1}, y_{0} ) + H_{c} (y_{0}, q_{2}, y_{1}) \right] \\
&\longrightarrow y_{2} q_{4} + \lambda \left[ H_{c} (q_{0}, q_{1}, y_{0} ) + H_{c} (y_{0}, q_{2}, y_{1}) + H_{c} (y_{1}, q_{3}, y_{2}) \right],
\quad \vec{y} \in \{ 0, 1 \} ^{3}.
\end{align}
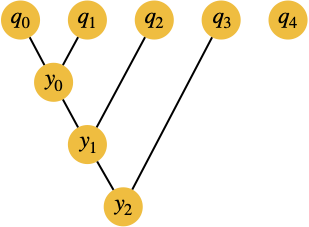
最終的に、QUBO変数が3個追加されました。制約条件を追加していく過程を図示すると、以下のようになります。
$q_{0}$と$q_{1}$の積を$y_{0}$で定義し、$y_{0}$と$q_{2}$の積を$y_{1}$で定義し...と左から順に積を新しく追加したQUBO変数で置き換えています。追加したQUBO変数が満たすべき制約条件は、$N=3$のときに定義した$H_{c}$で表現します。
制約条件を用いた次数下げを一般化する
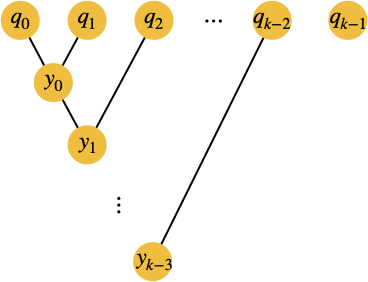
ここまで$N=3,4,5$の場合を見てきましたが、法則性から制約条件を一般化できそうです。先程の図を使って表現すると、以下のようになります。
$k$次式を2次式に次数下げするためには、$k-2$個のQUBO変数を追加し、制約条件項を付け加える必要があることが分かります。制約条件を含めたQUBOは以下のように書けます。$0$から$k-4$まで和を取っている項は、$N=3$の場合には登場しないことに注意してください。
H(\vec{q}) = \prod _{i=0} ^{k-1} q_{i}
\longrightarrow
H(\vec{q}; \vec{y}) =
y_{k-3} q_{k-1}
+ \lambda \left[ H_{c} \left(q_{0}, q_{1}, y_{0}\right) + \sum _{j=0}^{k-4} H_{c} \left( y_{j}, q_{j+2}, y_{j+1} \right) \right], \quad \vec{y} \in \{ 0, 1 \}^{k-2} .
シミュレータで確認する
制約条件項を加えたQUBOで正しく動作するのか、シミュレータで確認してみます。dwave-ocean-sdkを使い、ソルバーにはdimodとdwave-nealをそれぞれ指定して、同じように動作することを確認しました。
N=3の場合
まずは$N=3$の場合ですが、以下のQUBOをインプットにしました。パラメータ$\lambda$は$1$としました。
H(\vec{q}) = q_{0}q_{1}q_{2} \longrightarrow y_{0}q_{2} + H_{c} (q_{0}, q_{1}, y_{0}).
結果は以下のようになりました。先頭の3桁が$q_{0}, q_{1}, q_{2}$に対応しています。半角スペースを開けた後の1桁が、$y_{0}$に対応します。
110 1
011 0
100 0
101 0
010 0
001 0
000 0
$N=3$の場合、組み合わせは$2^{3}=8$通りありますが、そのうち$q_{0}q_{1}q_{2}=1$となるパターン以外が網羅されています。期待した通りの動作になっていますね。
N=10の場合
値を飛ばして$N=10$を試してみましょう。結果は以下の通りです。
1100001010 10000000
1111010000 11100000
1010111010 00000000
1100101010 10000000
1111000101 11100000
0001101100 00000000
0101011111 00000000
1001101010 00000000
1011011101 00000000
0011101010 00000000
0110101100 00000000
1110001001 11000000
1111111010 11111100
1100010000 10000000
0110011011 00000000
1111010100 11100000
0111001111 00000000
0000000000 00000000
全パターンは網羅されませんが、$\prod _{i=0}^{9} q _{i} =1$のパターンは登場していないので、これも成功です。この場合も$\lambda=1$としました。
結論
多項式を2次式に次数下げしてQUBOに変換することは、
-
QUBO変数の追加
-
制約条件項$H _{c}$の追加
によって実現できます。変換前の$k$次式を
H(\vec{q}) = \prod _{i=0} ^{k-1} q_{i}, \quad \vec{q} \in \{ 0, 1 \} ^{k}
とすると、QUBOは正のパラメータ$\lambda$を使って以下のように書けます。
H(\vec{q}) = \prod _{i=0} ^{k-1} q_{i} \longrightarrow
H(\vec{q}; \vec{y}) = y_{k-3} q_{k-1}
+ \lambda \left[ H_{c} \left(q_{0}, q_{1}, y_{0}\right) + \sum _{j=0}^{k-4} H_{c} \left( y_{j}, q_{j+2}, y_{j+1} \right) \right], \quad \vec{y} \in \{ 0, 1 \} ^{k-2} .
ただし、
H_{c}(x,y,z) = xy - 2(x+y) z + 3z
です。
おわりに
シミュレータで確認も行ったのでおそらく正しいだろうと思いつつ、色々と不備があるかもしれません。お手数ですが、何かお気づきの方はコメントいただければと思います。
-
パラメータの取り方は一意には決まりません。例えば$a=2$, $b+d=1$を仮定して、$b=-3, d=4$などとすることもできます。 ↩