【ラビットチャレンジ】深層学習(Day4:強化学習)

4_1_tensorflow_codes

#constant

import tensorflow as tf
import numpy as np

# それぞれ定数を定義
a = tf.constant(1)
b = tf.constant(2, dtype=tf.float32, shape=[3,2])
c = tf.constant(np.arange(4), dtype=tf.float32, shape=[2,2])

print('a:', a)
print('b:', b)
print('c:', c)

sess = tf.Session()

print('a:', sess.run(a))
print('b:', sess.run(b))
print('c:', sess.run(c))

a: Tensor("Const_3:0", shape=(), dtype=int32)
b: Tensor("Const_4:0", shape=(3, 2), dtype=float32)
c: Tensor("Const_5:0", shape=(2, 2), dtype=float32)
a: 1
b: [[2. 2.]
 [2. 2.]
 [2. 2.]]
c: [[0. 1.]
 [2. 3.]]

#placeholder
#後から自在に値を変えることができる。値を入れる箱のイメージ
#xをバッチ毎に代入するときによく使われる

import tensorflow as tf
import numpy as np

# プレースホルダーを定義
x = tf.placeholder(dtype=tf.float32, shape=[None,3])

print('x:', x)

sess = tf.Session()

X = np.random.rand(2,3)
print('X:', X)

# プレースホルダにX[0]を入力
# shapeを(3,)から(1,3)にするためreshape
print('x:', sess.run(x, feed_dict={x:X[0].reshape(1,-1)}))
# プレースホルダにX[1]を入力
print('x:', sess.run(x, feed_dict={x:X[1].reshape(1,-1)}))

x: Tensor("Placeholder:0", shape=(?, 3), dtype=float32)
X: [[0.72845236 0.90635957 0.89028197]
 [0.195471   0.57672833 0.62216894]]
x: [[0.7284524  0.90635955 0.890282  ]]
x: [[0.195471   0.57672834 0.62216896]]

#variables

# 定数を定義
a = tf.constant(10)
print('a:', a)
# 変数を定義
x = tf.Variable(1)
print('x:', x)

calc_op = x * a

print ('calc_op',calc_op)

# xの値を更新
update_x = tf.assign(x, calc_op)

sess = tf.Session()

# 変数の初期化
init = tf.global_variables_initializer()
sess.run(init)

print(sess.run(x))

sess.run(update_x)
print(sess.run(x))

sess.run(update_x)
print(sess.run(x)))

a: Tensor("Const_7:0", shape=(), dtype=int32)
x: <tf.Variable 'Variable_1:0' shape=() dtype=int32_ref>
calc_op Tensor("mul_1:0", shape=(), dtype=int32)
1
10
100

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

iters_num = 300
plot_interval = 10
#何学習ごとに誤差を出すか

# データを生成
n = 100
x = np.random.rand(n)
d = 3 * x + 2

# ノイズを加える
noise = 0.3
d = d + noise * np.random.randn(n) 

# 入力値
xt = tf.placeholder(tf.float32)
dt = tf.placeholder(tf.float32)

# 最適化の対象の変数を初期化
W = tf.Variable(tf.zeros([1]))
b = tf.Variable(tf.zeros([1]))

y = W * xt + b

# 誤差関数 平均2乗誤差
loss = tf.reduce_mean(tf.square(y - dt))
optimizer = tf.train.GradientDescentOptimizer(0.1)
train = optimizer.minimize(loss)

# 初期化
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

# 作成したデータをトレーニングデータとして準備
x_train = x.reshape(-1,1)
d_train = d.reshape(-1,1)

# トレーニング
for i in range(iters_num):
    sess.run(train, feed_dict={xt:x_train,dt:d_train})
    if (i+1) % plot_interval == 0:
        loss_val = sess.run(loss, feed_dict={xt:x_train,dt:d_train}) 
        W_val = sess.run(W)
        b_val = sess.run(b)
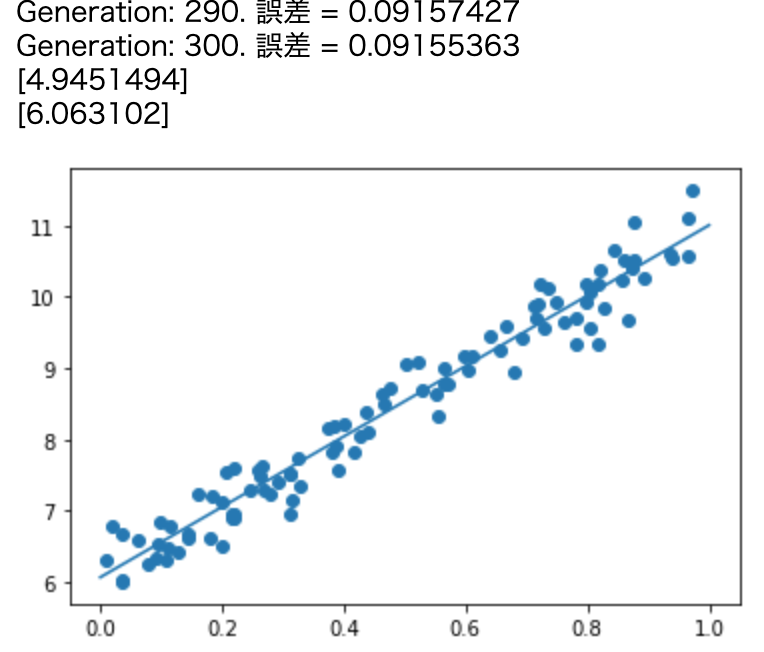
        print('Generation: ' + str(i+1) + '. 誤差 = ' + str(loss_val))

print(W_val)
print(b_val)

#  予測関数
def predict(x):
    return W_val * x + b_val

fig = plt.figure()
subplot = fig.add_subplot(1, 1, 1)
plt.scatter(x, d)
linex = np.linspace(0, 1, 2)
liney = predict(linex)
subplot.plot(linex,liney)
plt.show()

Generation: 10. 誤差 = 0.31117848
Generation: 20. 誤差 = 0.22165476
Generation: 30. 誤差 = 0.18499129
Generation: 40. 誤差 = 0.15758781
Generation: 50. 誤差 = 0.1370309
Generation: 60. 誤差 = 0.12160983
Generation: 70. 誤差 = 0.11004148
Generation: 80. 誤差 = 0.10136328
Generation: 90. 誤差 = 0.09485321
Generation: 100. 誤差 = 0.08996957
Generation: 110. 誤差 = 0.086306006
Generation: 120. 誤差 = 0.08355774
Generation: 130. 誤差 = 0.08149611
Generation: 140. 誤差 = 0.07994952
Generation: 150. 誤差 = 0.07878932
Generation: 160. 誤差 = 0.077918984
Generation: 170. 誤差 = 0.077266075
Generation: 180. 誤差 = 0.07677631
Generation: 190. 誤差 = 0.07640888
Generation: 200. 誤差 = 0.076133266
Generation: 210. 誤差 = 0.07592651
Generation: 220. 誤差 = 0.07577139
Generation: 230. 誤差 = 0.07565503
Generation: 240. 誤差 = 0.07556775
Generation: 250. 誤差 = 0.07550226
Generation: 260. 誤差 = 0.07545314
Generation: 270. 誤差 = 0.075416304
Generation: 280. 誤差 = 0.07538865
Generation: 290. 誤差 = 0.075367935
Generation: 300. 誤差 = 0.075352356
[3.1188667]
[1.9609197]

#Wは4つ
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

iters_num = 10000
plot_interval = 100

# データを生成
n=100
x = np.random.rand(n).astype(np.float32) * 4 - 2
d =  - 0.4 * x ** 3 + 1.6 * x ** 2 - 2.8 * x + 1

#  ノイズを加える
noise = 0.05
d = d + noise * np.random.randn(n) 

# モデル
# bを使っていないことに注意.
xt = tf.placeholder(tf.float32, [None, 4])
dt = tf.placeholder(tf.float32, [None, 1])
W = tf.Variable(tf.random_normal([4, 1], stddev=0.01))
#ウェイト4つ標準偏差0.01のランダムな値
y = tf.matmul(xt,W)

# 誤差関数 平均２乗誤差
loss = tf.reduce_mean(tf.square(y - dt))
optimizer = tf.train.AdamOptimizer(0.001)
train = optimizer.minimize(loss)

# 初期化
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

# 作成したデータをトレーニングデータとして準備
d_train = d.reshape(-1,1)
x_train = np.zeros([n, 4])
for i in range(n):
    for j in range(4):
        x_train[i, j] = x[i]**j

#  トレーニング
for i in range(iters_num):
    if (i+1) % plot_interval == 0:
        loss_val = sess.run(loss, feed_dict={xt:x_train, dt:d_train}) 
        W_val = sess.run(W)
        print('Generation: ' + str(i+1) + '. 誤差 = ' + str(loss_val))
    sess.run(train, feed_dict={xt:x_train,dt:d_train})

print(W_val[::-1])
    
# 予測関数
def predict(x):
    result = 0.
    for i in range(0,4):
        result += W_val[i,0] * x ** i
    return result

fig = plt.figure()
subplot = fig.add_subplot(1,1,1)
plt.scatter(x ,d)
linex = np.linspace(-2,2,100)
liney = predict(linex)
subplot.plot(linex,liney)
plt.show()

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

iters_num = 8000
plot_interval = 1000

# データを生成
n=100
x = np.random.rand(n).astype(np.float32) * 4 - 2
#d =  - 0.4 * x ** 3 + 1.6 * x ** 2 - 2.8 * x + 1
d =  30 * x ** 2 + 0.5 * x  + 0.2

#  ノイズを加える
#noise = 0.05
#d = d + noise * np.random.randn(n) 

# モデル
# bを使っていないことに注意.
xt = tf.placeholder(tf.float32, [None, 3])
dt = tf.placeholder(tf.float32, [None, 1])
W = tf.Variable(tf.random_normal([3, 1], stddev=0.01))
y = tf.matmul(xt,W)

# 誤差関数 平均２乗誤差
loss = tf.reduce_mean(tf.square(y - dt))
optimizer = tf.train.AdamOptimizer(0.05)
train = optimizer.minimize(loss)

# 初期化
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

# 作成したデータをトレーニングデータとして準備
d_train = d.reshape(-1,1)
x_train = np.zeros([n, 3])
for i in range(n):
    for j in range(3):
        x_train[i, j] = x[i]**j

#  トレーニング
for i in range(iters_num):
    if (i+1) % plot_interval == 0:
        loss_val = sess.run(loss, feed_dict={xt:x_train, dt:d_train}) 
        W_val = sess.run(W)
        print('Generation: ' + str(i+1) + '. 誤差 = ' + str(loss_val))
    sess.run(train, feed_dict={xt:x_train,dt:d_train})

print(W_val[::-1])
    
# 予測関数
def predict(x):
    result = 0.
    for i in range(0,3):
        result += W_val[i,0] * x ** i
    return result

fig = plt.figure()
subplot = fig.add_subplot(1,1,1)
plt.scatter(x ,d)
linex = np.linspace(-2,2,100)
liney = predict(linex)
subplot.plot(linex,liney)
plt.show()

import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

iters_num = 100
batch_size = 100
plot_interval = 1

# -------------- ここを補填 ------------------------
#28×28
x = tf.placeholder(tf.float32, [None, 784])
#0-9の分類
d = tf.placeholder(tf.float32, [None, 10])
W = tf.Variable(tf.random_normal([784, 10], stddev=0.01))
b = tf.Variable(tf.zeros([10]))
# ------------------------------------------------------

y = tf.nn.softmax(tf.matmul(x, W) + b)

# 交差エントロピー
cross_entropy = -tf.reduce_sum(d * tf.log(y), reduction_indices=[1])
loss = tf.reduce_mean(cross_entropy)
train = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

# 正誤を保存
correct = tf.equal(tf.argmax(y, 1), tf.argmax(d, 1))
# 正解率
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

accuracies = []
for i in range(iters_num):
    x_batch, d_batch = mnist.train.next_batch(batch_size)
    sess.run(train, feed_dict={x: x_batch, d: d_batch})
    if (i+1) % plot_interval == 0:
        print(sess.run(correct, feed_dict={x: mnist.test.images, d: mnist.test.labels}))
        accuracy_val = sess.run(accuracy, feed_dict={x: mnist.test.images, d: mnist.test.labels})
        accuracies.append(accuracy_val)
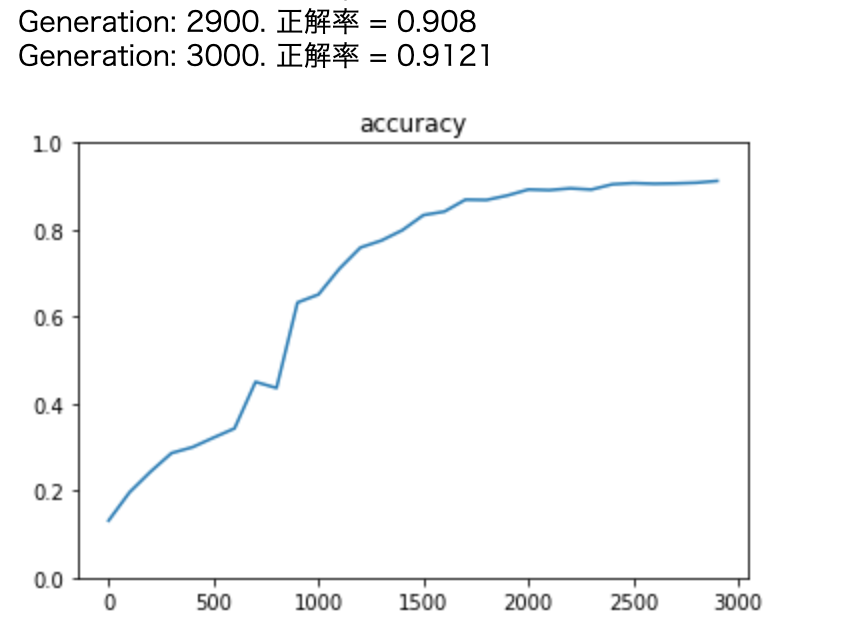
        print('Generation: ' + str(i+1) + '. 正解率 = ' + str(accuracy_val))
        
        
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies)
plt.title("accuracy")
plt.ylim(0, 1.0)
plt.show()        

import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

iters_num = 3000
batch_size = 100
plot_interval = 100

hidden_layer_size_1 = 600
hidden_layer_size_2 = 300
#784->600->300->10

dropout_rate = 0.5

x = tf.placeholder(tf.float32, [None, 784])
d = tf.placeholder(tf.float32, [None, 10])
W1 = tf.Variable(tf.random_normal([784, hidden_layer_size_1], stddev=0.01))
W2 = tf.Variable(tf.random_normal([hidden_layer_size_1, hidden_layer_size_2], stddev=0.01))
W3 = tf.Variable(tf.random_normal([hidden_layer_size_2, 10], stddev=0.01))

b1 = tf.Variable(tf.zeros([hidden_layer_size_1]))
b2 = tf.Variable(tf.zeros([hidden_layer_size_2]))
b3 = tf.Variable(tf.zeros([10]))

z1 = tf.sigmoid(tf.matmul(x, W1) + b1)
z2 = tf.sigmoid(tf.matmul(z1, W2) + b2)

keep_prob = tf.placeholder(tf.float32)
drop = tf.nn.dropout(z2, keep_prob)

y = tf.nn.softmax(tf.matmul(drop, W3) + b3)
loss = tf.reduce_mean(-tf.reduce_sum(d * tf.log(y), reduction_indices=[1]))


optimizer = tf.train.AdamOptimizer(1e-4)

train = optimizer.minimize(loss)
correct = tf.equal(tf.argmax(y, 1), tf.argmax(d, 1))
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

accuracies = []
for i in range(iters_num):
    x_batch, d_batch = mnist.train.next_batch(batch_size)
    sess.run(train, feed_dict={x:x_batch, d:d_batch, keep_prob:(1 - dropout_rate)})
    if (i+1) % plot_interval == 0:
        accuracy_val = sess.run(accuracy, feed_dict={x:mnist.test.images, d:mnist.test.labels, keep_prob:1.0})   #1.0を渡すことでdropoutさせない         
        accuracies.append(accuracy_val)
        print('Generation: ' + str(i+1) + '. 正解率 = ' + str(accuracy_val))        
    
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies)
plt.title("accuracy")
plt.ylim(0, 1.0)
plt.show()            

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
import matplotlib.pyplot as plt

iters_num = 300
batch_size = 100
plot_interval = 10

dropout_rate = 0.5

# placeholder
x = tf.placeholder(tf.float32, shape=[None, 784])
d = tf.placeholder(tf.float32, shape=[None, 10])

# 画像を784の一次元から28x28の二次元に変換する
# 画像を28x28にreshape
x_image = tf.reshape(x, [-1,28,28,1])

# 第一層のweightsとbiasのvariable
W_conv1 = tf.Variable(tf.truncated_normal([5, 5, 1, 32], stddev=0.1))
# 5×5のフィルタ。1~32チャンネル
b_conv1 = tf.Variable(tf.constant(0.1, shape=[32]))

# 第一層のconvolutionalとpool
# strides[0] = strides[3] = 1固定
h_conv1 = tf.nn.relu(tf.nn.conv2d(x_image, W_conv1, strides=[1, 1, 1, 1], padding='SAME') + b_conv1)
# プーリングサイズ n*n にしたい場合 ksize=[1, n, n, 1]
h_pool1 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

# 第二層
W_conv2 = tf.Variable(tf.truncated_normal([5, 5, 32, 64], stddev=0.1))
b_conv2 = tf.Variable(tf.constant(0.1, shape=[64]))
h_conv2 = tf.nn.relu(tf.nn.conv2d(h_pool1, W_conv2, strides=[1, 1, 1, 1], padding='SAME') + b_conv2)
h_pool2 = tf.nn.max_pool(h_conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

# 第一層と第二層でreduceされてできた特徴に対してrelu
W_fc1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1024], stddev=0.1))
#7×7×64
b_fc1 = tf.Variable(tf.constant(0.1, shape=[1024]))
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

# Dropout
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

# 出来上がったものに対してSoftmax
W_fc2 = tf.Variable(tf.truncated_normal([1024, 10], stddev=0.1))
b_fc2 = tf.Variable(tf.constant(0.1, shape=[10]))
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

# 交差エントロピー
loss = -tf.reduce_sum(d * tf.log(y_conv))

train = tf.train.AdamOptimizer(1e-4).minimize(loss)

correct = tf.equal(tf.argmax(y_conv,1), tf.argmax(d,1))
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)


accuracies = []
for i in range(iters_num):
    x_batch, d_batch = mnist.train.next_batch(batch_size)
    sess.run(train, feed_dict={x: x_batch, d: d_batch, keep_prob: 1-dropout_rate})
    if (i+1) % plot_interval == 0:
        accuracy_val = sess.run(accuracy, feed_dict={x:x_batch, d: d_batch, keep_prob: 1.0})
        accuracies.append(accuracy_val)
        print('Generation: ' + str(i+1) + '. 正解率 = ' + str(accuracy_val))        
    
    
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies)
plt.title("accuracy")
plt.ylim(0, 1.0)
plt.show()                

4_3_keras_codes

import numpy as np
import matplotlib.pyplot as plt

iters_num = 1000
plot_interval = 10

x = np.linspace(-1, 1, 200)
np.random.shuffle(x)
d = 0.5 * x + 2 + np.random.normal(0, 0.05, (200,))

from keras.models import Sequential
from keras.layers import Dense

# モデルを作成
model = Sequential()
model.add(Dense(input_dim=1, output_dim=1))

# モデルを表示
model.summary()

# モデルのコンパイル
model.compile(loss='mse', optimizer='sgd')

# train
for i in range(iters_num):
    loss = model.train_on_batch(x, d)
    if (i+1) % plot_interval == 0:
        print('Generation: ' + str(i+1) + '. 誤差 = ' + str(loss))

W, b = model.layers[0].get_weights()
print('W:', W)
print('b:', b)

y = model.predict(x)
plt.scatter(x, d)
plt.plot(x, y)
plt.show()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_1 (Dense)              (None, 1)                 2         
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________

# モジュール読み込み
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras.optimizers import SGD
 
# 乱数を固定値で初期化
np.random.seed(0)
# np.random.seed(1)

# シグモイドの単純パーセプトロン作成
model = Sequential()
model.add(Dense(input_dim=2, units=1))
model.add(Activation('sigmoid'))
model.summary()

model.compile(loss='binary_crossentropy', optimizer=SGD(lr=0.1))
 
# トレーニング用入力 X と正解データ T
X = np.array( [[0,0], [0,1], [1,0], [1,1]] )

#OR
T = np.array( [[0], [1], [1], [1]] )
#AND
# T = np.array( [[0], [0], [0], [1]] )
#XOR
# T = np.array( [[0], [1], [1], [0]] )

# トレーニング
model.fit(X, T, epochs=30, batch_size=1)
 
# トレーニングの入力を流用して実際に分類
Y = model.predict_classes(X, batch_size=1)

print("TEST")
print(Y == T)

Model: "sequential_3"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_3 (Dense)              (None, 1)                 3         
_________________________________________________________________
activation_2 (Activation)    (None, 1)                 0         
=================================================================
Total params: 3
Trainable params: 3
Non-trainable params: 0
_________________________________________________________________
Epoch 1/30
4/4 [==============================] - 0s 22ms/step - loss: 0.4352
Epoch 2/30
4/4 [==============================] - 0s 1ms/step - loss: 0.4204
Epoch 3/30
4/4 [==============================] - 0s 2ms/step - loss: 0.4079
Epoch 4/30
4/4 [==============================] - 0s 2ms/step - loss: 0.3971
Epoch 5/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3876
Epoch 6/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3790
Epoch 7/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3717
Epoch 8/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3650
Epoch 9/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3586
Epoch 10/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3528
Epoch 11/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3476
Epoch 12/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3425
Epoch 13/30
4/4 [==============================] - 0s 2ms/step - loss: 0.3378
Epoch 14/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3333
Epoch 15/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3291
Epoch 16/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3250
Epoch 17/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3210
Epoch 18/30
4/4 [==============================] - 0s 2ms/step - loss: 0.3172
Epoch 19/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3136
Epoch 20/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3100
Epoch 21/30
4/4 [==============================] - 0s 2ms/step - loss: 0.3067
Epoch 22/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3032
Epoch 23/30
4/4 [==============================] - 0s 1ms/step - loss: 0.3000
Epoch 24/30
4/4 [==============================] - 0s 1ms/step - loss: 0.2968
Epoch 25/30
4/4 [==============================] - 0s 1ms/step - loss: 0.2938
Epoch 26/30
4/4 [==============================] - 0s 1ms/step - loss: 0.2908
Epoch 27/30
4/4 [==============================] - 0s 1ms/step - loss: 0.2878
Epoch 28/30
4/4 [==============================] - 0s 2ms/step - loss: 0.2850
Epoch 29/30
4/4 [==============================] - 0s 2ms/step - loss: 0.2821
Epoch 30/30
4/4 [==============================] - 0s 2ms/step - loss: 0.2794
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

Epoch 29/30
4/4 [==============================] - 0s 980us/step - loss: 0.2991
Epoch 30/30
4/4 [==============================] - 0s 1ms/step - loss: 0.2961
TEST
[[False]
 [ True]
 [ True]
 [ True]]

#np.random.seed(0)

Epoch 100/100
4/4 [==============================] - 0s 1ms/step - loss: 0.1640
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

#np.random.seed(1)

Epoch 100/100
4/4 [==============================] - 0s 1ms/step - loss: 0.1715
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

#np.random.seed(0)  And
Epoch 100/100
4/4 [==============================] - 0s 1ms/step - loss: 0.2457
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

#np.random.seed(1) And
 
Epoch 100/100
4/4 [==============================] - 0s 1ms/step - loss: 0.2527
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

#np.random.seed(0)  XOR
Epoch 100/100
4/4 [==============================] - 0s 1ms/step - loss: 0.7195
TEST
[[ True]
 [ True]
 [False]
 [False]]

#np.random.seed(1) XOR

Epoch 100/100
4/4 [==============================] - 0s 1ms/step - loss: 0.7196
TEST
[[ True]
 [False]
 [ True]
 [False]]

#np.random.seed(0)
Epoch 30/30
4/4 [==============================] - 0s 386us/step - loss: 0.3594
TEST
[[False]
 [ True]
 [ True]
 [ True]]
#np.random.seed(1)
Epoch 30/30
4/4 [==============================] - 0s 256us/step - loss: 0.3874
TEST
[[False]
 [ True]
 [ True]
 [ True]]

#np.random.seed(0)

Epoch 300/300
4/4 [==============================] - 0s 1ms/step - loss: 0.0722
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

#np.random.seed(1)

Epoch 300/300
4/4 [==============================] - 0s 1ms/step - loss: 0.0739
TEST
[[ True]
 [ True]
 [ True]
 [ True]]

#XOR

Epoch 299/300
4/4 [==============================] - 0s 1ms/step - loss: 0.7187
Epoch 300/300
4/4 [==============================] - 0s 1ms/step - loss: 0.7190
TEST
[[False]
 [False]
 [ True]
 [ True]]

%matplotlib inline
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
x = iris.data
d = iris.target

from sklearn.model_selection import train_test_split
x_train, x_test, d_train, d_test = train_test_split(x, d, test_size=0.2)
#train 0.8, test 0.2

from keras.models import Sequential
from keras.layers import Dense, Activation
# from keras.optimizers import SGD

#モデルの設定
model = Sequential()
model.add(Dense(12, input_dim=4))
#入力4 中間層12

model.add(Activation('relu'))
# model.add(Activation('sigmoid'))
model.add(Dense(3, input_dim=12))
model.add(Activation('softmax'))
model.summary()

model.compile(optimizer='sgd', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

history = model.fit(x_train, d_train, batch_size=5, epochs=20, verbose=1, validation_data=(x_test, d_test))
loss = model.evaluate(x_test, d_test, verbose=0)

#print(history.history)

#Accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.ylim(0, 1.0)
plt.show()

Model: "sequential_26"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_35 (Dense)             (None, 12)                60        
_________________________________________________________________
activation_35 (Activation)   (None, 12)                0         
_________________________________________________________________
dense_36 (Dense)             (None, 3)                 39        
_________________________________________________________________
activation_36 (Activation)   (None, 3)                 0         
=================================================================
Total params: 99
Trainable params: 99
Non-trainable params: 0
_________________________________________________________________
Train on 120 samples, validate on 30 samples
Epoch 1/20
120/120 [==============================] - 0s 3ms/step - loss: 1.4307 - accuracy: 0.3000 - val_loss: 0.9220 - val_accuracy: 0.3667
Epoch 2/20
120/120 [==============================] - 0s 278us/step - loss: 0.8610 - accuracy: 0.5667 - val_loss: 0.8394 - val_accuracy: 0.7000
Epoch 3/20
120/120 [==============================] - 0s 293us/step - loss: 0.7606 - accuracy: 0.6750 - val_loss: 0.6464 - val_accuracy: 0.7333
Epoch 4/20
120/120 [==============================] - 0s 274us/step - loss: 0.6395 - accuracy: 0.6917 - val_loss: 0.6388 - val_accuracy: 0.6667
Epoch 5/20
120/120 [==============================] - 0s 283us/step - loss: 0.5760 - accuracy: 0.7583 - val_loss: 0.5394 - val_accuracy: 0.8667
Epoch 6/20
120/120 [==============================] - 0s 248us/step - loss: 0.5719 - accuracy: 0.7167 - val_loss: 0.4985 - val_accuracy: 0.8667
Epoch 7/20
120/120 [==============================] - 0s 262us/step - loss: 0.5038 - accuracy: 0.7833 - val_loss: 0.4596 - val_accuracy: 0.9333
Epoch 8/20
120/120 [==============================] - 0s 249us/step - loss: 0.4652 - accuracy: 0.8417 - val_loss: 0.4528 - val_accuracy: 0.7333
Epoch 9/20
120/120 [==============================] - 0s 236us/step - loss: 0.4379 - accuracy: 0.8000 - val_loss: 0.4016 - val_accuracy: 0.9000
Epoch 10/20
120/120 [==============================] - 0s 269us/step - loss: 0.4239 - accuracy: 0.8500 - val_loss: 0.3931 - val_accuracy: 0.8000
Epoch 11/20
120/120 [==============================] - 0s 229us/step - loss: 0.3983 - accuracy: 0.8583 - val_loss: 0.3794 - val_accuracy: 0.9000
Epoch 12/20
120/120 [==============================] - 0s 237us/step - loss: 0.3664 - accuracy: 0.8833 - val_loss: 0.3521 - val_accuracy: 0.9000
Epoch 13/20
120/120 [==============================] - 0s 236us/step - loss: 0.3705 - accuracy: 0.8583 - val_loss: 0.3291 - val_accuracy: 0.9667
Epoch 14/20
120/120 [==============================] - 0s 237us/step - loss: 0.3485 - accuracy: 0.9083 - val_loss: 0.3246 - val_accuracy: 0.9333
Epoch 15/20
120/120 [==============================] - 0s 231us/step - loss: 0.3472 - accuracy: 0.8667 - val_loss: 0.3136 - val_accuracy: 0.9667
Epoch 16/20
120/120 [==============================] - 0s 233us/step - loss: 0.3418 - accuracy: 0.8833 - val_loss: 0.3229 - val_accuracy: 0.9000
Epoch 17/20
120/120 [==============================] - 0s 238us/step - loss: 0.3132 - accuracy: 0.9250 - val_loss: 0.2929 - val_accuracy: 0.9667
Epoch 18/20
120/120 [==============================] - 0s 234us/step - loss: 0.3017 - accuracy: 0.9250 - val_loss: 0.3151 - val_accuracy: 0.8667
Epoch 19/20
120/120 [==============================] - 0s 263us/step - loss: 0.2877 - accuracy: 0.9083 - val_loss: 0.3263 - val_accuracy: 0.8000
Epoch 20/20
120/120 [==============================] - 0s 288us/step - loss: 0.2829 - accuracy: 0.9250 - val_loss: 0.2907 - val_accuracy: 0.9333

# 必要なライブラリのインポート
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import keras
import matplotlib.pyplot as plt
from data.mnist import load_mnist

(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

# 必要なライブラリのインポート、最適化手法はAdamを使う
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import Adam

# モデル作成
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(0.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(10, activation='softmax'))
model.summary()

# バッチサイズ、エポック数
batch_size = 128
epochs = 20

model.compile(loss='categorical_crossentropy', 
#               optimizer=Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False), 
              optimizer=Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, decay=0.0, amsgrad=False), 
              metrics=['accuracy'])

history = model.fit(x_train, d_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, d_test))
loss = model.evaluate(x_test, d_test, verbose=0)
print('Test loss:', loss[0])
print('Test accuracy:', loss[1])
#Accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
# plt.ylim(0, 1.0)
plt.show()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_10 (Dense)             (None, 512)               401920    
_________________________________________________________________
dropout_7 (Dropout)          (None, 512)               0         
_________________________________________________________________
dense_11 (Dense)             (None, 512)               262656    
_________________________________________________________________
dropout_8 (Dropout)          (None, 512)               0         
_________________________________________________________________
dense_12 (Dense)             (None, 10)                5130      
=================================================================
Total params: 669,706
Trainable params: 669,706
Non-trainable params: 0
_________________________________________________________________
Train on 60000 samples, validate on 10000 samples
Epoch 1/20
60000/60000 [==============================] - 4s 61us/step - loss: 0.2503 - accuracy: 0.9241 - val_loss: 0.1097 - val_accuracy: 0.9637
Epoch 2/20
60000/60000 [==============================] - 4s 59us/step - loss: 0.1014 - accuracy: 0.9688 - val_loss: 0.0776 - val_accuracy: 0.9752
Epoch 3/20
60000/60000 [==============================] - 4s 63us/step - loss: 0.0731 - accuracy: 0.9768 - val_loss: 0.0685 - val_accuracy: 0.9781
Epoch 4/20
60000/60000 [==============================] - 4s 64us/step - loss: 0.0578 - accuracy: 0.9819 - val_loss: 0.0661 - val_accuracy: 0.9797
Epoch 5/20
60000/60000 [==============================] - 4s 62us/step - loss: 0.0458 - accuracy: 0.9855 - val_loss: 0.0668 - val_accuracy: 0.9803
Epoch 6/20
60000/60000 [==============================] - 4s 63us/step - loss: 0.0403 - accuracy: 0.9866 - val_loss: 0.0653 - val_accuracy: 0.9804
Epoch 7/20
60000/60000 [==============================] - 4s 68us/step - loss: 0.0342 - accuracy: 0.9890 - val_loss: 0.0730 - val_accuracy: 0.9809
Epoch 8/20
60000/60000 [==============================] - 4s 65us/step - loss: 0.0327 - accuracy: 0.9892 - val_loss: 0.0611 - val_accuracy: 0.9829
Epoch 9/20
60000/60000 [==============================] - 4s 73us/step - loss: 0.0265 - accuracy: 0.9906 - val_loss: 0.0646 - val_accuracy: 0.9826
Epoch 10/20
60000/60000 [==============================] - 4s 63us/step - loss: 0.0254 - accuracy: 0.9917 - val_loss: 0.0632 - val_accuracy: 0.9839
Epoch 11/20
60000/60000 [==============================] - 4s 64us/step - loss: 0.0220 - accuracy: 0.9924 - val_loss: 0.0753 - val_accuracy: 0.9820
Epoch 12/20
60000/60000 [==============================] - 4s 64us/step - loss: 0.0224 - accuracy: 0.9926 - val_loss: 0.0662 - val_accuracy: 0.9817
Epoch 13/20
60000/60000 [==============================] - 4s 60us/step - loss: 0.0192 - accuracy: 0.9935 - val_loss: 0.0680 - val_accuracy: 0.9812
Epoch 14/20
60000/60000 [==============================] - 4s 62us/step - loss: 0.0215 - accuracy: 0.9929 - val_loss: 0.0741 - val_accuracy: 0.9798
Epoch 15/20
60000/60000 [==============================] - 4s 66us/step - loss: 0.0187 - accuracy: 0.9936 - val_loss: 0.0725 - val_accuracy: 0.9835
Epoch 16/20
60000/60000 [==============================] - 4s 67us/step - loss: 0.0177 - accuracy: 0.9941 - val_loss: 0.0628 - val_accuracy: 0.9842
Epoch 17/20
60000/60000 [==============================] - 4s 69us/step - loss: 0.0164 - accuracy: 0.9945 - val_loss: 0.0702 - val_accuracy: 0.9840
Epoch 18/20
60000/60000 [==============================] - 4s 68us/step - loss: 0.0160 - accuracy: 0.9949 - val_loss: 0.0766 - val_accuracy: 0.9819
Epoch 19/20
60000/60000 [==============================] - 4s 66us/step - loss: 0.0168 - accuracy: 0.9942 - val_loss: 0.0706 - val_accuracy: 0.9834
Epoch 20/20
60000/60000 [==============================] - 4s 64us/step - loss: 0.0141 - accuracy: 0.9955 - val_loss: 0.0777 - val_accuracy: 0.9827
Test loss: 0.07771477883279009
Test accuracy: 0.982699990272522

# 必要なライブラリのインポート
import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import keras
import matplotlib.pyplot as plt
from data.mnist import load_mnist

(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)


# 行列として入力するための加工
batch_size = 128
num_classes = 10
epochs = 20

img_rows, img_cols = 28, 28

x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)
input_shape = (img_rows, img_cols, 1)


# 必要なライブラリのインポート、最適化手法はAdamを使う
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.optimizers import Adam

model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3),
                 activation='relu',
                 input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.summary()

# バッチサイズ、エポック数
batch_size = 128
epochs = 20

model.compile(loss='categorical_crossentropy', optimizer=Adam(), metrics=['accuracy'])
history = model.fit(x_train, d_train, batch_size=batch_size, epochs=epochs, verbose=1, validation_data=(x_test, d_test))

#Accuracy
plt.plot(history.history['accuracy'])
plt.plot(history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
# plt.ylim(0, 1.0)
plt.show()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (None, 26, 26, 32)        320       
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 24, 24, 64)        18496     
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 12, 12, 64)        0         
_________________________________________________________________
dropout_23 (Dropout)         (None, 12, 12, 64)        0         
_________________________________________________________________
flatten_1 (Flatten)          (None, 9216)              0         
_________________________________________________________________
dense_34 (Dense)             (None, 128)               1179776   
_________________________________________________________________
dropout_24 (Dropout)         (None, 128)               0         
_________________________________________________________________
dense_35 (Dense)             (None, 10)                1290      
=================================================================
Total params: 1,199,882
Trainable params: 1,199,882
Non-trainable params: 0
_________________________________________________________________
Train on 60000 samples, validate on 10000 samples
Epoch 1/20
60000/60000 [==============================] - 74s 1ms/step - loss: 0.2500 - accuracy: 0.9238 - val_loss: 0.0547 - val_accuracy: 0.9820
Epoch 2/20
60000/60000 [==============================] - 92s 2ms/step - loss: 0.0909 - accuracy: 0.9721 - val_loss: 0.0392 - val_accuracy: 0.9871
Epoch 3/20
60000/60000 [==============================] - 84s 1ms/step - loss: 0.0671 - accuracy: 0.9801 - val_loss: 0.0360 - val_accuracy: 0.9875
Epoch 4/20
60000/60000 [==============================] - 81s 1ms/step - loss: 0.0557 - accuracy: 0.9830 - val_loss: 0.0315 - val_accuracy: 0.9897
Epoch 5/20
60000/60000 [==============================] - 154s 3ms/step - loss: 0.0459 - accuracy: 0.9859 - val_loss: 0.0308 - val_accuracy: 0.9900
Epoch 6/20
60000/60000 [==============================] - 126s 2ms/step - loss: 0.0384 - accuracy: 0.9881 - val_loss: 0.0293 - val_accuracy: 0.9914
Epoch 7/20
60000/60000 [==============================] - 138s 2ms/step - loss: 0.0344 - accuracy: 0.9886 - val_loss: 0.0295 - val_accuracy: 0.9911
Epoch 8/20
60000/60000 [==============================] - 189s 3ms/step - loss: 0.0310 - accuracy: 0.9901 - val_loss: 0.0280 - val_accuracy: 0.9921
Epoch 9/20
60000/60000 [==============================] - 139s 2ms/step - loss: 0.0292 - accuracy: 0.9905 - val_loss: 0.0302 - val_accuracy: 0.9911
Epoch 10/20
60000/60000 [==============================] - 87s 1ms/step - loss: 0.0248 - accuracy: 0.9921 - val_loss: 0.0286 - val_accuracy: 0.9918
Epoch 11/20
60000/60000 [==============================] - 77s 1ms/step - loss: 0.0243 - accuracy: 0.9920 - val_loss: 0.0261 - val_accuracy: 0.9918
Epoch 12/20
60000/60000 [==============================] - 176s 3ms/step - loss: 0.0213 - accuracy: 0.9926 - val_loss: 0.0277 - val_accuracy: 0.9923
Epoch 13/20
60000/60000 [==============================] - 101s 2ms/step - loss: 0.0205 - accuracy: 0.9930 - val_loss: 0.0243 - val_accuracy: 0.9936
Epoch 14/20
60000/60000 [==============================] - 74s 1ms/step - loss: 0.0194 - accuracy: 0.9934 - val_loss: 0.0305 - val_accuracy: 0.9919
Epoch 15/20
60000/60000 [==============================] - 76s 1ms/step - loss: 0.0181 - accuracy: 0.9941 - val_loss: 0.0295 - val_accuracy: 0.9930
Epoch 16/20
60000/60000 [==============================] - 78s 1ms/step - loss: 0.0161 - accuracy: 0.9944 - val_loss: 0.0289 - val_accuracy: 0.9931
Epoch 17/20
60000/60000 [==============================] - 77s 1ms/step - loss: 0.0159 - accuracy: 0.9946 - val_loss: 0.0302 - val_accuracy: 0.9926
Epoch 18/20
60000/60000 [==============================] - 77s 1ms/step - loss: 0.0141 - accuracy: 0.9956 - val_loss: 0.0284 - val_accuracy: 0.9926
Epoch 19/20
60000/60000 [==============================] - 76s 1ms/step - loss: 0.0144 - accuracy: 0.9949 - val_loss: 0.0277 - val_accuracy: 0.9936
Epoch 20/20
60000/60000 [==============================] - 77s 1ms/step - loss: 0.0148 - accuracy: 0.9951 - val_loss: 0.0314 - val_accuracy: 0.9918