はじめに
Qiitaをよく使います。
しかし、私はQiitaを書いたことがありません。
恥ずかしいですねー
これから、自分自身の勉強のため、Qiitaでいろいろなことを書きたいと思っています。
自分の書いたものが他の方の参考になれば幸せです。
そうなれるように頑張ります。
最近、社内勉強会に参加しました。
この勉強会は、輪講の形で実施しています。
「Rによる統計的学習の入門」という教科書を使っています。
下記のURLで教科書の購入ができます。
https://www.asakura.co.jp/books/isbn/978-4-254-12224-4/
今回の投稿内容は、この教科書の演習問題3.7(4)の自分の解答です。
それでは、早速見ていきましょう。
1.演習問題
1.1.問題
この演習問題は、「Rによる統計的学習の入門」から引用します。
(4)応答変数と1つの予測変数について100個(n=100)のデータを観測した。線形回帰と、3次多項式での回帰$𝑌=\beta_0+\beta_1 𝑋+\beta_2 𝑋^2+\beta_3 𝑋^3+\epsilon$をそれぞれ当てはめた。
(a) 𝑋と𝑌の真の関係が$𝑌=\beta_0+\beta_1 𝑋+\epsilon$であるとする。線形単回帰を当てはめたときの訓練RSSと3次式の回帰における訓練RSSを考えた場合、どちらの方がより小さくなるといえるか。両方等しくなると考えられるか。または、情報不足により判断できないか。説明せよ。
(b) (a)において、テストRSSを比べた場合について答えよ。
(c) 𝑋と𝑌の真の関係は線形ではないと仮定する。しかし、どの程度非線形かは未知である。線形単回帰を当てはめたときの訓練RSSと3次式の回帰における訓練RSSを考えた場合、どちらの方がより小さくなるといえるか。両方等しくなると考えられるか。または情報不足により判断できないか。説明せよ。
(d) (c)において、テストRSSを比べた場合について答えよ。
1.2.概念紹介
この問題を解くために必要な概念を紹介します。
1.2.1.線形回帰問題とは何か?
まず、回帰問題は、データから誤差を織り込んだ入出力関係を推定する問題です。ここで、出力は応答変数、入力は予測変数と言います。
線形回帰は、教師あり学習の一つです。線形回帰では、線形単回帰と線形重回帰二つのアプローチがあります。この二つのアプローチの違いは、簡単に言えば、予測変数の数が異なります。線形単回帰の場合は一つ、線形重回帰の場合は二つ以上です。二つのアプローチの名称では、両方「線形」という言葉がついています。しかし、線形重回帰の場合では、非線形性への拡張ができます。
1.2.2.線形単回帰とは何か?
量的応答変数を単一の予測変数によって予測しようというアプローチです。イメージしにくいと思うので、式(1)で説明します。式(1)が示すように、xは入力すなわち予測変数、yは出力すなわち応答変数です。$\beta_0$は切片といい、つまりx=0の時のyの期待値です。$\beta_1$は傾きといい、つまりxが1増加したときのyの増加量です。$\epsilon$は、誤差です。
y = \beta_0 + \beta_1 x + ε \tag{1}
ここで、応答変数yを予測変数xによって予測しようとします。観測データを使用することによって、$\beta_0$ 、$\beta_1$の値を算出することができます。観測データを測定するとき、誤差が生じる可能性があるという考えで、誤差$\epsilon$は式に入れました。通常、誤差$\epsilon$は予測変数xと独立していると仮定します。
1.2.3.線形重回帰とは何か?
量的応答変数yを二つ以上の予測変数$x_1$,$x_2$,…によって予測しようというアプローチです。式(2)に示すように、線形重回帰と線形単回帰との違いは、予測変数の数です。
y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ⋯ + \epsilon \tag{2}
演習問題の中で、「3次多項式での回帰」という言葉がありましたが、それは線形重回帰の一つのパターンという認識で問題ありません。
1.2.4.残差平方和とは何か?
線形回帰では、モデルを学習させます。ここでの学習とは、観測データによって切片と傾きを調整することです。どのように調整するのか、評価指標が必要です。残差平方和は一つの評価指標としてよく使われています。残差平方和は、観測データと推定モデルとの差異を評価する尺度です。英語の省略はRSS (Residual Sum of Squares)です。式(3)により残差平方和の算出ができます。$y_i$は観測データ、$y_i$は予測変数$x_i$により予測された予測値です。RSSの値が小さくなると、学習モデルの精度は高くなります。
RSS= \sum(y_i-y ̂_i )^2 \tag{3}
2.解答
問題を解くために必要な概念の説明はここまでです。
それでは、もう一度問題を見ましょう。
実は、この問題が聞きたいのは、表1の中での各条件で、線形単回帰と3次多項式での回帰、線形重回帰のRSSの値の大小関係です。すなわち、線形単回帰、線形重回帰は各条件で、どちらのモデルの精度が良いのかという質問です。
表1. 問題内容と解答
| 応答変数と予測変数の真の関係 | 線形性 | 非線形性 | ||
|---|---|---|---|---|
| 訓練時/テスト時 | 訓練時 | テスト時 | 訓練時 | テスト時 |
| 線形単回帰RSS Vs 3次多項式回帰RSS | ① | ③ | ⑤ | ⑦ |
| 理由 | ② | ④ | ⑥ | ⑧ |
①回帰における訓練RSSの値は線形単回帰を当てはめたときの訓練RSSより小さくなると言えます。
②線形単回帰と、3次多項式回帰をそれぞれ当てはめた時、3次多項式の方の回帰曲線は線形単回帰の回帰直線より予測変数の微小変動を捉えます。
③線形単回帰を当てはめたときのテストRSSは3次式の回帰におけるテストRSSより小さくなると言えます。
④訓練において、3次多項式の方の回帰曲線は線形単回帰の回帰直線より予測変数の微小変動を捉えますが、過学習が起こり得ます。線形単回帰の場合では、発生しません。
⑤3次式の回帰における訓練RSSは線形単回帰を当てはめたときの訓練RSSより小さくなると言えます。
⑥線形単回帰と、3次多項式回帰をそれぞれ当てはめた時、3次多項式の方の回帰曲線は線形単回帰の回帰直線より予測変数の微小変動を捉えます。
⑦情報不足により判断できません。
⑧XとYの真の関係は線形ではないと仮定します。しかし、どの程度非線形かは未知です。XとYの真の関係は線形と近づければ、線形単回帰を当てはめた時のテストRSSは、3次式の回帰におけるテストRSSより小さくなると言えます。XとYの真の関係は非線形と近づければ、3次式の回帰におけるテストRSSは、線形単回帰を当てはめた時のテストRSSより小さくなると言えます。
3. Rによる検証
演習問題(a)の内容をRStudio Desktopで検証します。
3.1. Rコード
検証実験を実施する時、観測データが必要です。今回の観測データは、応答変数と予測変数の真の関係$Y = \beta_0 + \beta_1X + \epsilon$に基づいて作成しました。Rソースコードの詳細は以下となります。
# ランダムに100個の観測データを作成します。
x <- 1:100
y <- 1 + 2*x + rnorm(100, mean = 10, sd = 2)
# 観測データをデータフレームに変換します。
xy <- data.frame(x,y)
# 観測データをプロットします。
plot(xy)
# 線形単回帰場合での回帰を行います。
lm.fitA <- lm(y~x, data=xy)
# データの特徴を集計します。
summary(lm.fitA)
# 残差平方和RSSを算出します。
deviance(lm.fitA)
# 3次多項式場合での回帰を行います。
lm.fitB <- lm(y~x+I(x^2)+I(x^3), data=xy)
# データの特徴を集計します。
summary(lm.fitB)
# 残差平方和RSSを算出します。
deviance(lm.fitB)
3.2. 実行結果
自作の観測データを、以下の図に示します。
縦軸は応答変数y、横軸は予測変数xです。
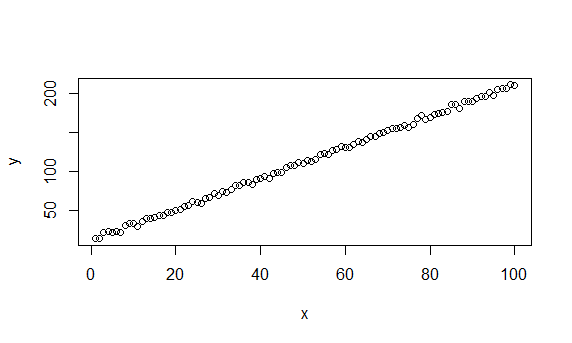
> # ランダムに100個の観測データを作成します。
> x <- 1:100
> y <- 1 + x*2 + rnorm(100, mean = 10, sd = 2)
>
> # 観測データをデータフレームに変換します。
> xy <- data.frame(x,y)
>
> # 観測データをプロットします。
> plot(xy)
>
> # 線形単回帰場合での回帰を行います。
> lm.fitA <- lm(y~x, data=xy)
>
> # データの特徴を集計します。
> summary(lm.fitA)
Call:
lm(formula = y ~ x, data = xy)
Residuals:
Min 1Q Median 3Q Max
-4.8167 -1.5275 0.0368 1.6421 4.5547
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.197201 0.424163 26.4 <2e-16 ***
x 1.995952 0.007292 273.7 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.105 on 98 degrees of freedom
Multiple R-squared: 0.9987, Adjusted R-squared: 0.9987
F-statistic: 7.492e+04 on 1 and 98 DF, p-value: < 2.2e-16
>
> # 残差平方和RSSを算出します。
> deviance(lm.fitA)
[1] 434.2108
>
> # 3次多項式場合での回帰を行います。
> lm.fitB <- lm(y~x+I(x^2)+I(x^3), data=xy)
>
> #データの特徴を集計します。
> summary(lm.fitB)
Call:
lm(formula = y ~ x + I(x^2) + I(x^3), data = xy)
Residuals:
Min 1Q Median 3Q Max
-4.9985 -1.3449 0.0055 1.6976 4.3623
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.202e+01 8.783e-01 13.689 <2e-16 ***
x 1.917e+00 7.494e-02 25.581 <2e-16 ***
I(x^2) 1.693e-03 1.719e-03 0.985 0.327
I(x^3) -1.005e-05 1.119e-05 -0.898 0.371
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.114 on 96 degrees of freedom
Multiple R-squared: 0.9987, Adjusted R-squared: 0.9987
F-statistic: 2.476e+04 on 3 and 96 DF, p-value: < 2.2e-16
>
> #残差平方和RSSを算出します。
> deviance(lm.fitB)
[1] 428.9941
実行結果を確認します。線形単回帰の場合と3次多項式の場合での残差平方和の値は、434.2108と428.9941です。訓練時で、3次多項式の場合は線形単回帰の場合より残差平方和が低かったことを確認できました。
4. 所感
統計学を勉強する時、いろいろな検証実験をすると思います。その時、観測データを自作する場合が多いです。どのように観測データを作れば適切と言えるのか、検証実験を実施する前に考慮する必要があります。
参考書籍
1.著者 G. James,D. Witten,T. Hastie,R. Tibshirani,(2017),原著タイトル,An Introduction to Statistical Learning: with Applications in R.訳者 落海 浩,首藤 信通,(2018),Rによる統計的学習の入門,朝倉書店.
以上です。