More than 5 years have passed since last update.

【論文】Filter Response Normalization Layer: Eliminating Batch Dependence in the Training of Deep Neural Networks

Last updated at 2019-12-04Posted at 2019-12-02

【論文編】では論文の軽いまとめを掲載します
~~【検証編】では PyTorch を使って実装してみて効果が期待できそうか確認をします(作成中)~~
- あまりまともな精度が出なかったのでやめます(すみません)
- 実装: https://github.com/yukkyo/FilterResponseNormalizationLayer-PyTorch

0. 導入

今話題の [1911.09737] Filter Response Normalization Layer: Eliminating Batch Dependence in the Training of Deep Neural Networks について読んでみました。

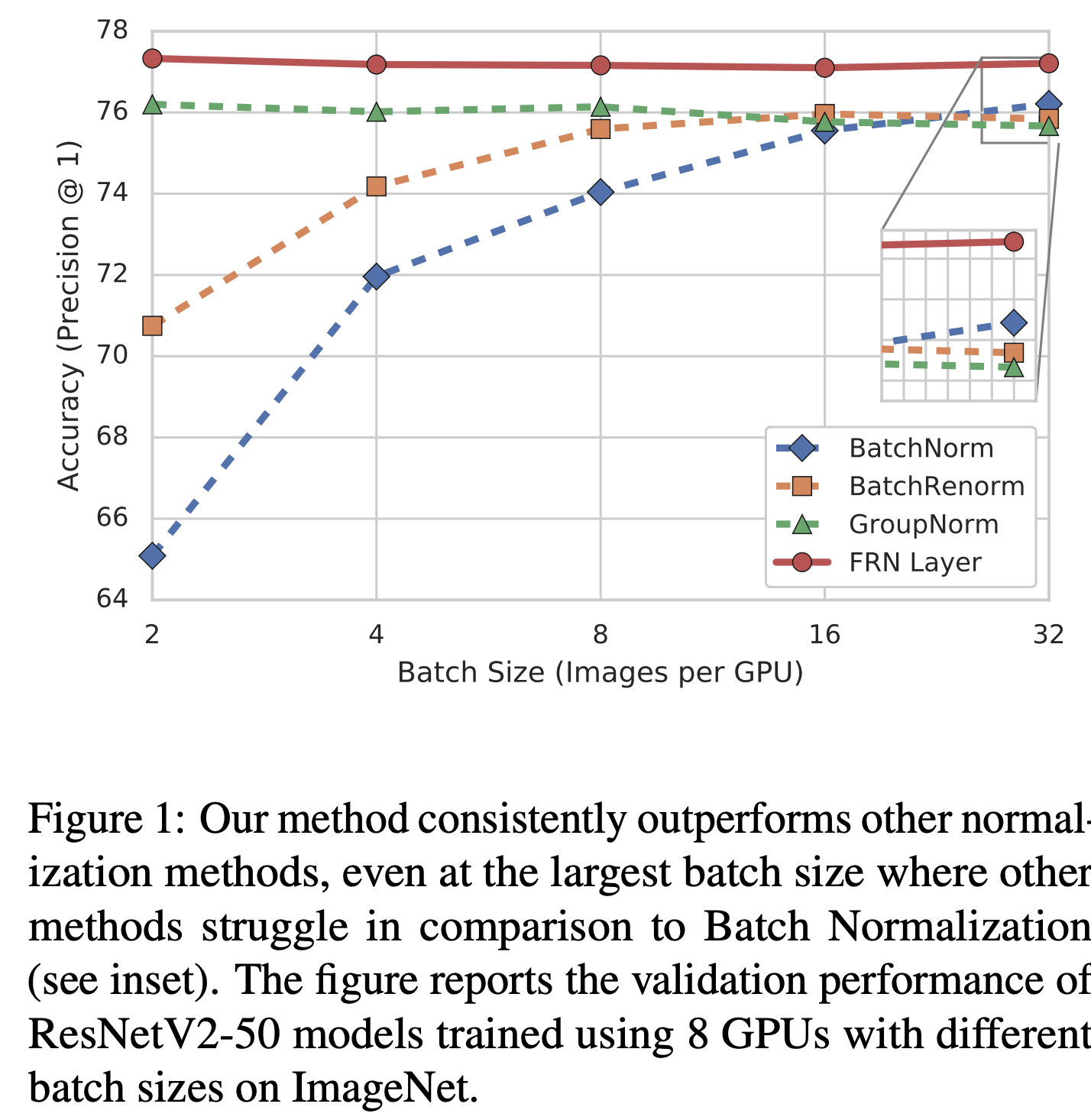
上記は Classification の実験結果らしいですが、高そうですね。
むしろここまで来ると高すぎて逆に怪しいですね。

1. 論文まとめ

1.1 Abstract & Conclusion

Batch Normalization(BN)¹ はぐう優秀
- でも mini-batch の統計情報に依存するので batch-size が小さかったり sample 間に相関があると悪影響がある
- それらに対処するため Batch Renormalization(BR)² とか Group Normalization(GN)³ とかが提案されている
- ただし下記のような課題が残っている
  - 大規模 Batch Size の BN のパフォーマンスと一致しない
  - 小規模 Batch Size でのパフォーマンス低下
  - モデルに対し人為的な制約が生じる
本論文では **Filter Response Normalization (FRN)**を提案する
- 正規化と活性化関数を組み合わせたもの
- 各バッチサンプルの各アクティベーションマップ上で独立して動作する（？）
  - 他のバッチサンプルまたは同じサンプルのチャネルへの依存を排除する（？）
- 既存の正規化(ex. BN) + 活性化関数(ex. ReLU)を置換して使える
- Batch Size 変えて色々実験したけど、いずれも BN より FRN の方が高かった
- BN に置き換わる Group Normalization よりも FRN の方が検証上良かった
各ドメインに応じて違う Normalization 方法が成功している(ex. NLP での Layer Normalization)
- それは今後検証していくとのこと

1.2 Introduction

BN はすごいけど BS 小さいと悪さするよね
BR² とか GN³ も提案されてるけど課題あるよね
- BR → 小さい BS での性能が良くない
- GN → モデルに制約が入る(Input Channel が BS の倍数であることが望ましい)
FRN の構成要素
- フィルター応答正規化（FRN）と呼ばれる正規化手法
  - 平均減算を実行せずに、各バッチサンプルの応答を非中心2次モーメントの平方根で除算することにより、独立して正規化する
    - チャンネルごとの正規化 をしている
- Thresholded Linear Unit (TLU)
  - learned rectification threshold を使い、ゼロから離れる方向にバイアスされるアクティベーションを可能にする
The main contributions in this paper
- Filter Response Normalization (FRN)
- The Thresholded Linear Unit (TLU)
- FRN と TLU の組み合わせの検証と精度向上の確認
- 様々な classification と object detection 手法に対する FRN+TLU の検証

1.3 Related work

whitening(白色化) とか Batch Normalization (BN) とかがある。ただし BN は BS が小さいときに悪さしやすい。
これらに対処する方法として以下の方法が提案されている。

batch normalized モデルの train-test 間の乖離を低減する
- Batch Renormalization (BR)²
  - train-test 間の統計量の不一致は、小さいバッチサイズや non-iid(独立でない)サンプルのバイアスによるものと仮定
  - ミニバッチモーメントを特定の範囲に制限し、トレーニング中のミニバッチ統計の変動を制限する
- Evalnorm⁴
  - training scheme を修正する代わりに evaluation 時の統計情報を修正する
  - モデルの re-training が不要なのがメリット
  - ただし BR と Evalnorm は小さい BS 時の精度が高くない
- 実装の工夫で大規模バッチを複数 GPU で処理する⁵
  - それ専用のインフラが必要になる
バッチ単位の正規化を回避するための Sample based normalization
- 平均と分散を計算するための範囲を変えることが多い(Batch 方向だけじゃなく他の方向でも集約させる)
  - その範囲の分布について、train・test は同一分布であるという仮定が置かれていることに注意
- 代表例
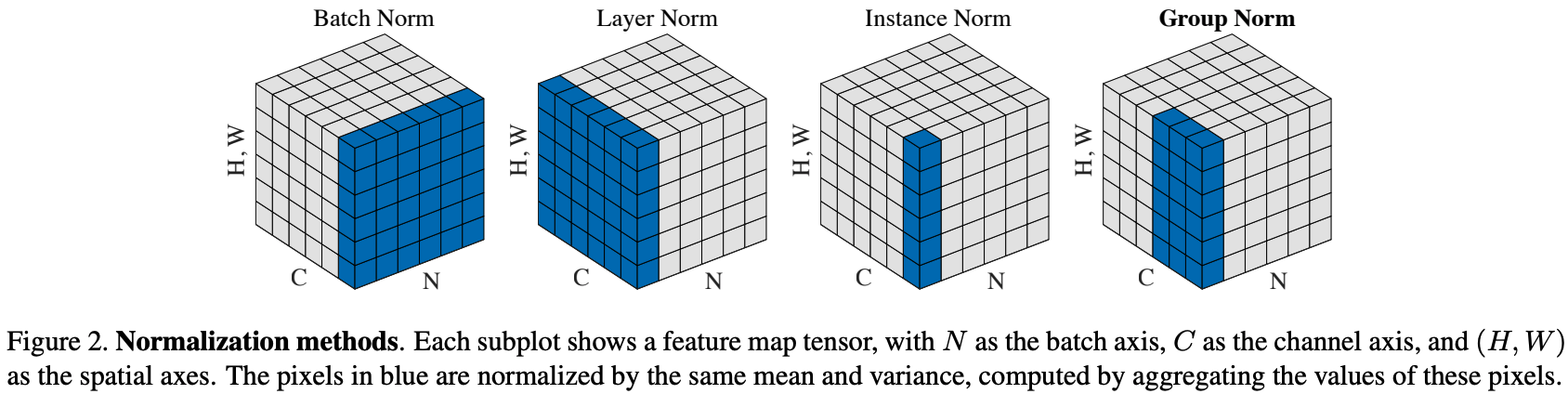
  - Layer Normalization (LN)⁶
    - 指定した BS 内の全 H・W・C について計算して正規化する
  - Instance Normalization (IN)⁷
    - BS は 1にして、各 Channel(C) も独立に計算する
      - BS を 1にした BN
    - Style Transfer では有用だったが、Recognition では成功事例を聞かない
  - Group Normalization (GN)³
    - 指定した BS 内全 H・W と C について計算するが、LN と違い Channel(C) をグループに分割する
    - Channel 数がグループ数の倍数である必要がある
    - グループ数は実験的に決める
    - ただし BS を大きくすると BN の方が良い

LN・IN・GN の比較は Group Normalization の論文³にあった下図が分かりやすいです。

1.4 Approach(一番大事なところ)

FRN Layer は下の図のように FRN と TLU で分けられます。
この図を見てティンと来てしまった人は飛ばしましょう。

また下図内の $\gamma, \beta, \epsilon, \tau$ は学習対象のパラメータです。　

1.4.1 Filter Response Normalization (FRN)

まず FRN Layer への入力を $\boldsymbol{X}$ とする
- $\boldsymbol{X}$ のサイズは $[\text{BatchSize}, \text{Width}, \text{Height}, \text{Channel}]$ とします
- PyTorch が Channel First(BS, CH, H, W) に対して Channel Last であることに注意
次に $\boldsymbol{x} = \boldsymbol{X}_{b, :, :, c} \in \mathbb{R}^{N}$ とする
- バッチのうち $b$ 番目の要素でかつ $c$ 番目の channel(filter) の要素
- $N = W \times H$
次に $\boldsymbol{x}$ の各要素を $x_i$ とし、$\nu^2 = \sum_{i}x_i^2 / N$ を計算する
- この値はスカラー
- ちょうど下図の青い部分の範囲について各要素を2乗して平均を取ることと同じ

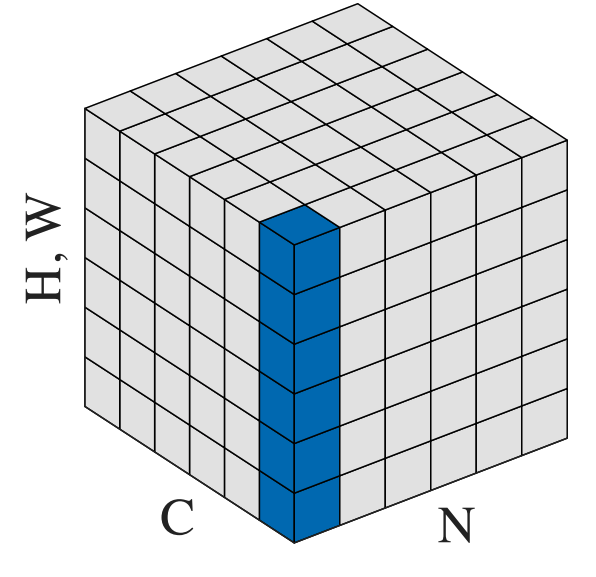
次に $\nu^2$ で $\boldsymbol{x}$ をスケーリングする

$$
\hat{\boldsymbol{x}} = \frac{\boldsymbol{x}}{\sqrt{\nu^2 + \epsilon}}
$$

次に $\boldsymbol{y} = \gamma \hat{\boldsymbol{x}} + \beta$ を計算します
- このときの $\gamma$ と $\beta$ はスカラーです
- ですので計算上は $\hat{\boldsymbol{x}}$ の各要素に対して $\gamma$ を掛けて $\beta$ を足しています
- また $\gamma$ と $\beta$ は Channel に対して共通です
  - ある $c$ において同じ値
  - なのでトータルとしての学習パラメータは $C$ 次元のベクトルになります
  - $\gamma_c$ とか $\beta_c$ の方が分かりやすいですね
TLU に入力する

1.4.2 The Thresholded Linear Unit (TLU)

TLU は見ての通り ReLU で書き換えられることがあります
また ReLU との違いとして、$\tau$ 自体が学習対象です

$$
z_i = \max (y_i, \tau) = \max(y_i - \tau, 0) + \tau = \text{ReLU}(y_i - \tau) + \tau
$$

1.4.3 実装

論文⁸内では TensorFlow によるコードが紹介されていますが、すごくシンプルです。

FRN_TensorFlow

def FRNLayer(x, tau, beta, gamma, eps=1e-6):
    # x: Input tensor of shape [BxHxWxC].
    # alpha, beta, gamma: Variables of shape [1, 1, 1, C].
    # eps: A scalar constant or learnable variable.
    # Compute the mean norm of activations per channel.
    nu2 = tf.reduce_mean(tf.square(x), axis=[1, 2], keepdims=True)

    # Perform FRN.
    x = x * tf.rsqrt(nu2 + tf.abs(eps))

    # Return after applying the Offset-ReLU non-linearity.
    return tf.maximum(gamma * x + beta, tau)

PyTorch 版実装は https://github.com/yukkyo/FilterResponseNormalizationLayer-PyTorch に置きました。

1.5 Experiments

元論文では幅広い実験をしていますがこの記事内では一部しか紹介しません。
気になる方は元論文⁸を確認しましょう

1.5.1 Classification(ImageNet)

Train でも Validation でも FRN が高いです
ただし立ち上がりでは FRN の方が低いです

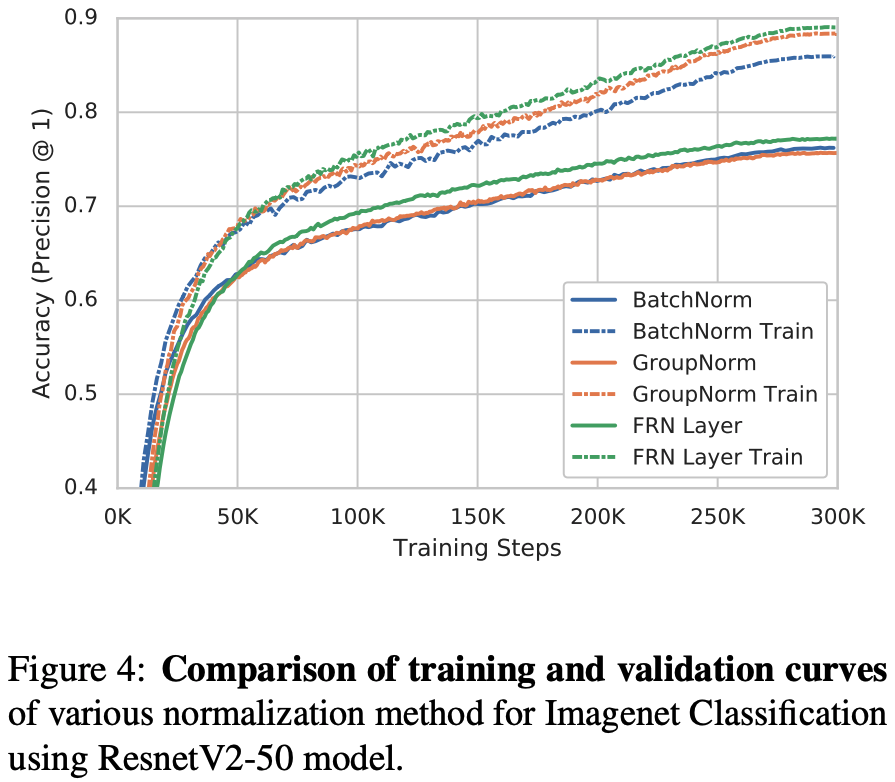
1.5.2 Ablation of our method on Imagenet Classification for ResnetV2-50 and InceptionV3

下の表では FRN と TLU をそれぞれ別に適用した場合と、メジャーな Normalize 手法(BN・GN・LN・IN)との比較を表しています。
また GN や LN に対し、BN のように "平均引いて分散で割る" 代わりに FRN のように "二次のモーメントで割った" ものをそれぞれ GFRN・LFRN としています。

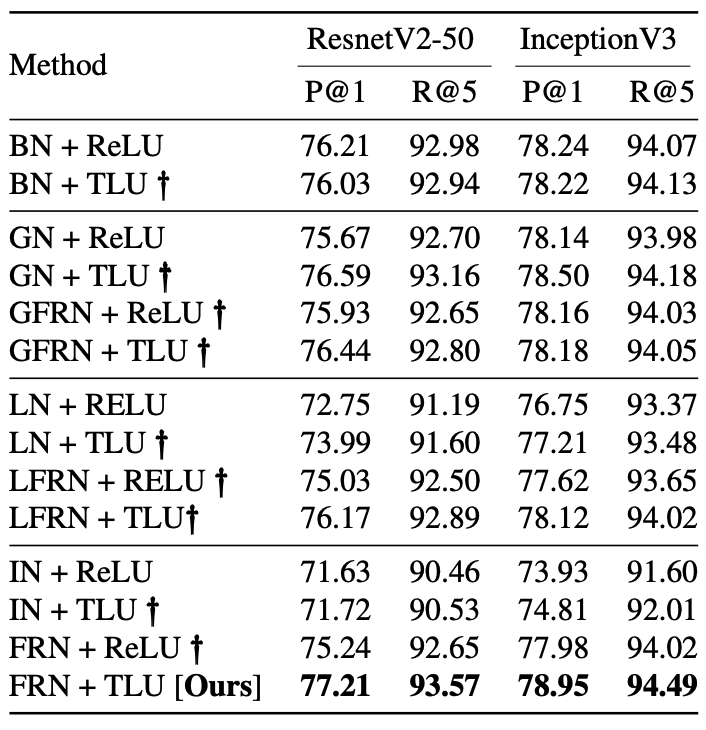
太字で見落としがちですけど、BN + ReLUでも結構な精度が出ているように見えます(他が低かったりする)。
また FRN+ReLU では BN+ReLU よりも 1% 程度低くなっており、FRN+TLU のセットでちゃんと効果が見込めそうみたいです。

1.5.3 Object Detection(Retina Net on COCO dataset)

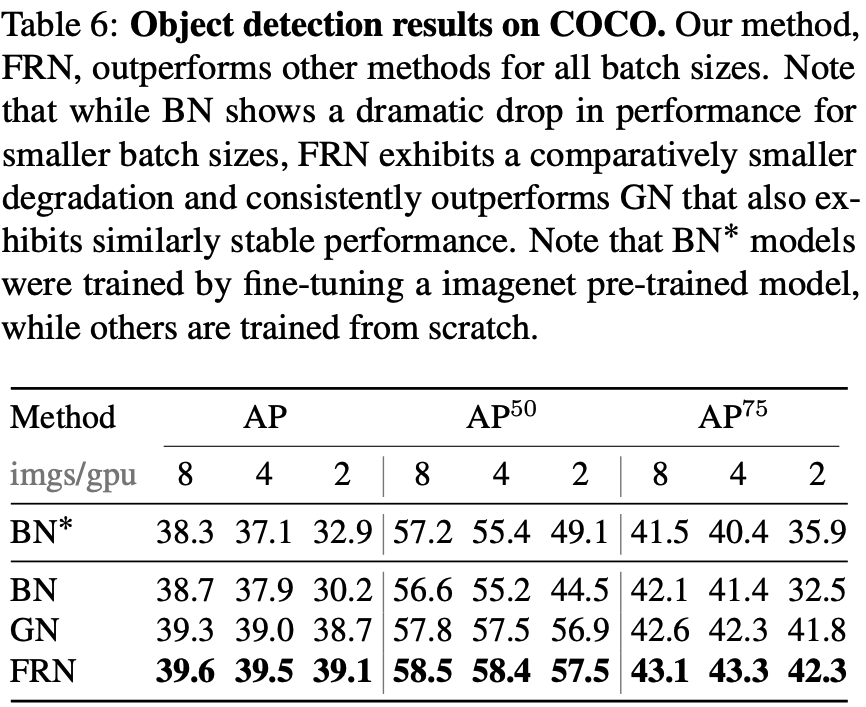
嬉しいことに Object Detection での比較も行われています。
注意事項として BN* は ImageNet pre-trained model から fine-tuning した結果です。
他の結果はスクラッチ学習したものです。いずれも FRN の方が良い結果となっています。
加えて興味深いのは、小さいBS(2)のときは ImageNet pre-train の効果があり、大きくなるほどスクラッチで学習した方が精度が高くなっていることですね。

まとめ

FRN はバッチの他の要素に依存しない(対象の 1サンプル)正規化ができる
- 必要なのは下記のパラメータのみ
  - チャンネル依存のスケールパラメータ $\gamma$ と $\beta$
  - 単一のスカラーである $\epsilon$
  - TLU で使う $\tau$(スカラー)
バッチサイズに依存しないので、小さい BS と大きい BS で性能が乖離しない
- Classification(ImageNet) ではほとんど変わらない
- Object Detection(COCO) では大きい BS の方が精度高いけど、BN ほど乖離していない
FRN は単体ではなくて TLU とセットで使ったほうが良さそう

参考文献・ページ

Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. CoRR, abs/1502.03167, 2015. ↩
Sergey Ioffe. Batch renormalization: Towards reducing minibatch dependence in batch-normalized models. In Advances in Neural Information Processing Systems, pages 1942–1950, 2017. ↩ ↩² ↩³
Yuxin Wu and Kaiming He. Group normalization. In Computer Vision and Pattern Recognition, 2018. ↩ ↩² ↩³ ↩⁴
Saurabh Singh and Abhinav Shrivastava. Evalnorm: Estimating batch normalization statistics for evaluation. In ICCV, 2019. ↩
Chao Peng, Tete Xiao, Zeming Li, Yuning Jiang, Xiangyu Zhang, Kai Jia, Gang Yu, and Jian Sun. Megdet: A large mini-batch object detector. In Computer Vision and Pattern Recognition, pages 6181–6189, 2018. ↩
Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E Hinton. Layer normalization. arXiv preprint arXiv:1607.06450, 2016. ↩
Dmitry Ulyanov, Andrea Vedaldi, and Victor Lempitsky. Instance normalization: The missing ingredient for fast stylization. arXiv preprint arXiv:1607.08022, 2016. ↩
[1911.09737] Filter Response Normalization Layer: Eliminating Batch Dependence in the Training of Deep Neural Networks ↩ ↩²

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up