LoginSignup
6
5

More than 5 years have passed since last update.

@expin株式会社Tsunagu.AI

とてもシンプルなAdamを実装する（ベクトル）

Last updated at Posted at 2019-02-02

ディープラーニングでよく使用されるソルバー、Adam (Kingma, Ba, 2015)を理解するためにpythonでシンプルな実装を行った。
以前、パラメータをスカラー$\theta$として同様の記事を書いたが(とてもシンプルなAdamを実装する（スカラー）)、今回はパラメータを2次元のベクトル$\vec{\theta} = (\theta_1, \theta_2) $とした。
モデルは$y=\theta_1 x_1 + \theta_2 x_2$、誤差関数は二乗誤差を使用した。

アルゴリズム

この節はスカラー版の記事と同じものを再掲した。

Adamの理論的な面について筆者は別に記事を書いている(俺はまだ本当のAdamを理解していない)。
Adamは生の勾配ではなく、勾配の平均と(中心化前の)分散を使って、パラメータの更新幅が大きくなりすぎないように調節していることが特徴だった。また、この平均と分散を0にバイアスさせない目的で定数$\beta_1,\beta_2$による補正を行っている。

Adamのアルゴリズムを再掲する。

アルゴリズム1

$g_t^2$は要素ごとの2乗$g_t \odot g_t $を表す。
ベクトル上のすべての操作は要素ごとに行う。
$\beta_1^t, \beta_2^t$は$\beta_1, \beta_2$の$t$乗のこと。

Require:$\quad \alpha \quad$ ステップサイズ
Require:$\quad \beta_1, \beta_2 \in [0,1) \quad$モーメント推定に使う指数減衰率
Require:$\quad f(\theta) \quad$ パラメターを$\theta$とする確率的目的関数
Require:$\quad \theta_0 \quad$ 初期パラメータベクトル
$\quad m_0 \leftarrow 0 \quad$(最初の一次モーメントベクトル)
$\quad v_0 \leftarrow 0 \quad$(最初の二次モーメントベクトル)
$\quad t \leftarrow 0 \quad$(タイムステップ初期化)
$\quad$ while $\;\theta_t$が収束していない do
$\qquad t \leftarrow t+1$
$\qquad g_t \leftarrow \nabla_\theta f_t (\theta_{t-1}) \quad$ 目的関数の時刻tでの勾配
$\qquad m_t \leftarrow \beta_1 \cdot m_{t-1} +(1-\beta_1) \cdot g_t \quad$ 一次のモーメントを更新（バイアスあり）
$\qquad v_t \leftarrow \beta_2 \cdot v_{t-1} + (1-\beta_2) \cdot g_t^2 \quad$　二次の生のモーメントを更新（バイアスあり）
$\qquad \hat{m_t} \leftarrow \frac{m_t}{(1-\beta_1^t)} \quad$ バイアス修正した一次のモーメント
$\qquad \hat{v_t} \leftarrow \frac{v_t}{(1-\beta_2^t)} \quad$　バイアス修正した二次の生のモーメント
$\qquad \theta_t \leftarrow \theta_{t-1} - \alpha \cdot \frac{\hat{m_t}}{\sqrt{\hat{v_t}+\epsilon}} \quad$　パラメータ更新
$\quad$end while
return $\theta_t$

アルゴリズムで使用される固定値の推奨設定：

\alpha=0.001 \\
\beta_1=0.9  \\
\beta_2=0.999 \\
\epsilon=10^{-8}

問題設定

冒頭にもある通り、最適化の対象はモデル

y=\theta_1 x_1 + \theta_2 x_2

の$\theta_1,\theta_2$である。これらはまとめて$\vec{\theta}=(\theta_1,\theta_2)^{\mathrm{T}}$と書ける。
最適な$\vec{\theta}$は

\theta_1=0.9 \\
\theta_2=2.9

となるようにする。
つまり、適当に$x_1, x_2$を選んで、$0.9 x_1 + 2.9 x_2$を正解としてデータセットを作り、ランダムな$\theta_1,\theta_2$から始めて、Adamで最適化する。

勾配計算

今回のモデルは$y=\theta_1 x_1 + \theta_2 x_2$である。今、説明のために$y$を$y'$と書き換える。つまり

y'=\theta_1 x_1 + \theta_2 x_2  \tag{1}

目的関数はこの出力$y'$に正解データ$y$との２乗誤差関数を適用した

f=(y' - y)^2 \tag{2}

である。
今回はパラメータが$\theta_1,\theta_2 $2つあるので、$(1)$式に注意してそれぞれに関して$(2)$式を偏微分すると、

\begin{align}
\frac {\partial f}{\partial \theta_1} & =2(y' - y)(\frac {\partial y'}{\partial \theta_1}) \\
&= 2(y' - y)(x_1) \tag{3}  \\

\frac {\partial f}{\partial \theta_2} & =2(y' - y)(\frac {\partial y'}{\partial \theta_2}) \\
&= 2(y' - y)(x_2) \tag{4}
\end{align}

$(3), (4)$式はそれぞれ$\theta_1$方向および$\theta_2$方向の傾きを示しており、2つ並べてベクトルにしたものが今回の勾配ベクトルとなる。

実装

アルゴリズム１の説明に、

ベクトル上のすべての操作は要素ごとに行う。

とある通りで、単純にパラメータを増やした分同じ計算を追加するだけで動作した。
増えたパラメータに対して同じ操作を繰り返せば良い。
コード的には汚い。

adam_vector.py
# -*- coding: utf-8 -*-
import math
import random

#定義
ALPHA=0.001 #ステップサイズ
BETA_1=0.9 #一次モーメントの指数減衰率
BETA_2=0.999 #二次モーメントの指数減衰率
THETA_0=random.random() #最適化するθの初期値
EPS=1e-08 #イプシロン
EPOCH=2000 #エポック数

#初期化------
m_0=0 #一次モーメント
m_t_old1=m_t_old2=m_0 #１時刻前の一次モーメント

v_0=0 #二次モーメント
v_t_old1=v_t_old2=v_0 #１時刻前の二次モーメント

t=0 #タイムステップ

#θ
theta_t1=theta_t2=THETA_0
theta_t_old1=theta_t_old2=THETA_0
theta_t_old=[theta_t_old1, theta_t_old2]


#モデル定義
#y(x1,x2,θ1,θ2 )=θ1* x1 + θ2* x2 
def calc_y(x,theta):
  """
  x: float list length=2
  theta: float list length=2
  """
  result =theta[0]*x[0]+theta[1]*x[1]
  return result

#上記のθ1微分
def dy_dtheta_1(x):
  """
  x: float list length=2
  """
  result=x[0]
  return result

#上記のθ2微分
def dy_dtheta_2(x):
  """
  x: float list length=2
  """
  result=x[1]
  return result

#2乗誤差
def error_func(x, y):
    """
      x: float
      y: float
    """
    subs=x-y
    result=pow(subs, 2)
    return result

#２乗誤差の微分
def df_dy(f, y):
    """
      f: float
      y: float
    """
    result=2*(f-y)
    return result


#可視化用------
gts=[]
mts=[]
vts=[]
mthats=[]
vthats=[]
thetas=[]
losses=[]


#データセット------
DS_X=[]
DS_y=[]
NUM_DATA=1000
RAND_MAX=10.0

# yとして、x1*0.9 + x2*2.9 を使う。
# θ1=0.9,  θ2=2.9
THETA_1=0.9
THETA_2=2.9
THETA=[THETA_1,THETA_2]

for i in range(NUM_DATA):
    x1=random.uniform(-RAND_MAX,RAND_MAX)
    x2=random.uniform(-RAND_MAX,RAND_MAX)
    x_=[x1,x2]
    ans=calc_y(x_,THETA)
    DS_X.append(x_)
    DS_y.append(ans) 


# 実行------
# 収束までではなくエポック数だけ回す
while  t<EPOCH :

    #データはランダムに送る
    idx=random.randint(0,NUM_DATA-1)
    x=DS_X[idx]
    y=DS_y[idx]

    #時刻増やす 
    t=t+1

    #目的関数の勾配g_t
    y_prime=calc_y(x,theta_t_old)
    g_t1=df_dy(y_prime,y)*dy_dtheta_1(x)
    g_t2=df_dy(y_prime,y)*dy_dtheta_2(x)
    gts.append([g_t1, g_t2])

    #誤差
    losses.append(error_func(y_prime, y))

    # 一次モーメントの更新
    # beta_1が大きいと過去の値が支配的になる
    m_t1=BETA_1*m_t_old1 + (1- BETA_1)* g_t1
    m_t2=BETA_1*m_t_old2 + (1- BETA_1)* g_t2
    mts.append([m_t1, m_t2])
    # 二次モーメントの更新
    v_t1=BETA_2*v_t_old1 + (1-BETA_2) * pow(g_t1, 2)
    v_t2=BETA_2*v_t_old2 + (1-BETA_2) * pow(g_t2, 2)
    vts.append([v_t1,v_t2])

    #一次モーメントのバイアス補正
    m_t_hat1=m_t1 / (1-pow(BETA_1, t))
    m_t_hat2=m_t2 / (1-pow(BETA_1, t))
    mthats.append([m_t_hat1, m_t_hat2])

    #二次モーメントのバイアス補正
    v_t_hat1=v_t1 / (1-pow(BETA_2, t))
    v_t_hat2=v_t2 / (1-pow(BETA_2, t))
    vthats.append([v_t_hat1, v_t_hat2])

    #パラメータθを更新
    theta_t1=theta_t_old1 -ALPHA * m_t_hat1 / (math.sqrt(v_t_hat1 + EPS)) 
    theta_t2=theta_t_old2 -ALPHA * m_t_hat2 / (math.sqrt(v_t_hat2 + EPS)) 
    #古いθとして保持
    theta_t_old1=theta_t1
    theta_t_old2=theta_t2
    theta_t_old=[theta_t_old1,theta_t_old2]
    thetas.append([theta_t1,theta_t2])


#結果
print("theta_t1:",theta_t1)
print("theta_t2:",theta_t2)

実行

Google Colabで実行した。

theta_t1: 0.899087570436904
theta_t2: 2.8986415952149556

こんな感じで、

\theta_1=0.9 \\
\theta_2=2.9

に近い値が出てくれば成功。

学習の可視化

次のようにグラフをプロットして確認した。横軸はタイムステップt。

ts=range(EPOCH)
plt.plot(ts, losses,  lw=0.4, alpha=0.7)

誤差以外のグラフは$\theta_1,\theta_2$に関する2つのグラフを重ねて表示している。

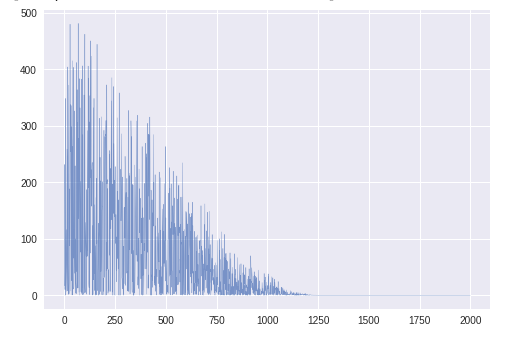
誤差


1200エポック程度で収束している。

パラメータθ1,θ2


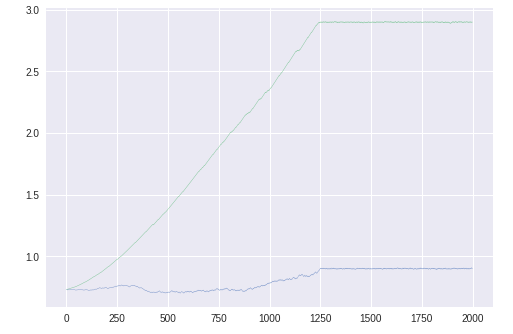
青いほうが$\theta_1$。青線が少しふらついているが、問題なく最適解に向かっているようである。

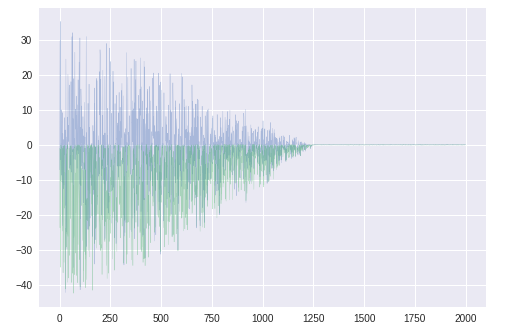
勾配gt


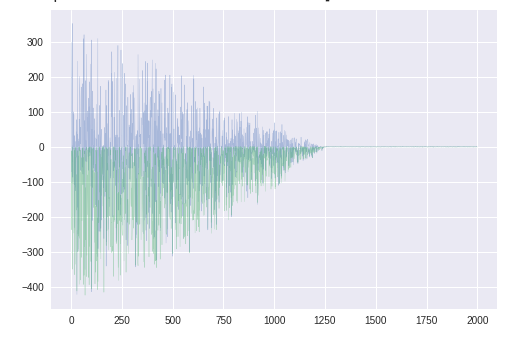
青いほうが$\theta_1$に関する勾配。$\theta_2$とは異なり、正負に振れがある。
$\theta$のグラフに見えるふらつきはこのためか。

勾配の平均mt


スケールが小さくなったが、形は$g_t$と類似。

バイアス補正した勾配の平均mt^


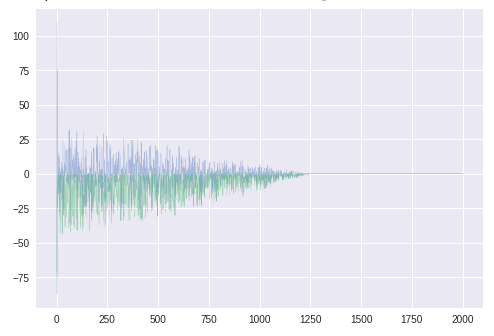
学習初期のみ値が大きく、以降は元より小さくなっている。前回、

0で初期化された学習初期だけ補正が強く働いている

と書いたが、やはりそのようである。
($\hat{m_t} \leftarrow \frac{m_t}{(1-\beta_1^t)}$で、$\beta_1^t$がどんどん小さくなるから、あとの方では補正が弱くなる)

勾配の分散vt


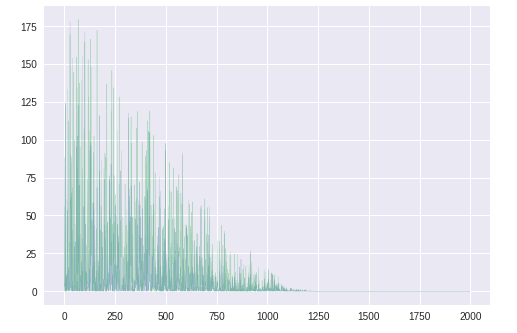
同じ方向を向いているのでわかりにくいが、
$\theta_2$に対応する緑色のほうが大きい。

バイアス補正した勾配の分散vt^


かなり補正されている。$\hat{m_t}$同様、後半に行くほど補正が弱まる。
$\hat{v_t} \leftarrow \frac{v_t}{(1-\beta_2^t)}$

更新幅の係数


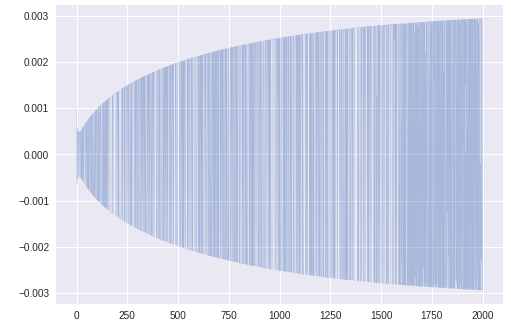
$\theta_1$更新のステップサイズを可視化したところ、このグラフが得られた。
これは次のコードで右辺の第２項の部分である。

 theta_t1=theta_t_old1 -ALPHA * m_t_hat1 / (math.sqrt(v_t_hat1 + EPS))

グラフを拡大すると

かなりふらついている。

まとめ

  • 2次元のパラメータベクトル$\vec{\theta} = (\theta_1, \theta_2) $に対して最適化を行うAdamをpythonで実装した
  • 目的関数はモデル$y=\theta_1 x_1 + \theta_2 x_2$に2乗誤差を適用したもの
  • パラメータ$\theta_1,\theta_2$の最適解への収束、Adamのバイアス補正の挙動等を確認できた。パラメータが複数でも問題なく動作することがわかった。

展望

  • Adam以外のソルバーとの比較
  • ニューラルネットワーク
6
5
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
6
5