The Past, Present, and Future of Multidimensional Scaling(Patrick J.F. Groenen, Ingwer Borg, 2013)(pdfのダウンロードリンク)を読んでいるので要約とメモ

元論文はMDS（多次元尺度構成法）について、マイルストーンとなる発展を述べたサーベイ。構成は、

基本アイデア
過去
技術的なこと
現在
未来

となっている。
長いので何本かに分ける。この記事はパート１で、２章までの内容。

筆者の理解と疑問を青色でメモしている。

本文

概要

多次元尺度構成法(Multidimensional scaling (MDS))は統計や応用科学者にとってスタンダードなツール。複雑な構造のデータを簡単に解釈できるから成功した。データは通常２次元に埋め込まれる。（品物、属性、刺激、反応などの）興味のある対象は埋め込まれた点に対応しており、近いもの同士は感覚的に似ていて、離れたものは異なるものとなる。本論文ではMDSの重要な開発者の何人かに敬意を表し、MDS発展のマイルストーンを主観的に概観する。MDSの現在の状況についても論じ、将来の見通しも少し述べる。

MDSは標準的なデータ解析・多変量解析・コンピュータサイエンスの教科書ならどれでも論じられる多変量解析テクニックのコアの一つとなった。Thomson Reuters Web of Scienceで“multidimensional scaling”を検索すると5,186の論文があり、68,429箇所で引用されている(2013.1時点)ことからも、MDSが確立された多変量解析手法であることがわかる。

マイルストーンになるような発展は区別できるし、本論文はそれを主観的に解釈する。MDSの歴史全てを網羅するものではない。それはそれだけで本になるのでBorg and Groenen (2005)を参照のこと。

本論文は時系列とトピックごとの両方から構成される。
大まかに時間を３つに区切っている
過去(1980まで), 現在(1980-2000), 未来(2000以降)
未来はもっと先のことを書くべきだが、開発したものが広く使われるにはいつでも時間がかかるものだ。だから約15年のラグがある2000からこの論文がかかれた2013までのラグ
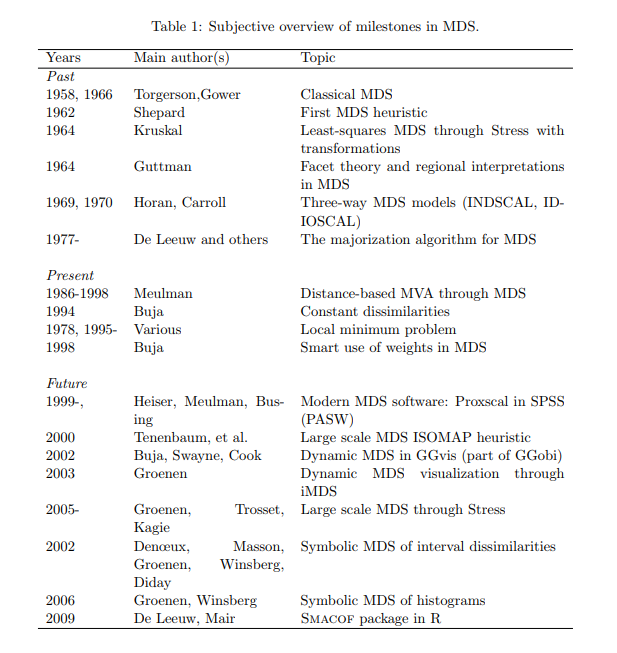
表1にマイルストーンの概要を示す。これらの詳細は次章以降。

表1

1. Multidimensional Scalingの基本アイデア

Borg and Groenen (2005)の最初の文でコアアイデアの説明がある。

MDSはオブジェクトペア間の類似度(または非類似度)の計測(measurements)を、低次元な多次元空間の点の間の距離として表現する手法である。

従って、通常のcases–by–variablesのデータの代わりに、MDSのデータはオブジェクトペア間の（非）類似度の計測から成り、まとめて"近さ(proximities)"と呼ぶ。オブジェクトは人、属性、刺激、国、等である。計測はテストアイテムの相関、政治家の類似度、携帯電話の非類似度、等でありうる。ゴールはこれらのオブジェクトを低次元空間(通常2次元)における点として表現することである。しかも、点の間の距離が可能な限り（非）類似度を表現するようにする。これの動機は、データを数字の行列よりもっとわかりやすい"絵"にすること。

古典的な例として、被験者が音響モールス信号をどのくらい間違うかを考える(Rothkopf, 1957)。ここでの研究課題は、何を間違えて、何を間違えないのかを決める心理学的なルールを発見すること。
　26個がアルファベットの文字、10個が数字からなる36個のモールス信号がある。被験者のタスクは特定ペアのモールス信号が"同じもの"か、"違うもの"かを判断すること。各ペアは2つの順序で示される：例えば最初にA(トン・ツーまたは'·−')、次にD(ツー・トン・トンまたは'− · ·')。そして最初にD、次にA。モールス信号が2つ1組ペアで示されて、その2つが同じ信号かどうかを判断する。このペア自体2回示される。示されるペア内の信号の順番は1回目と2回目では逆になっている
　モールス符号に詳しくない598人の被験者が351のペアを判定する。表2は完全な36x36行列の取り違え率を示す。confusion matrix

表2

このデータは類似度である。距離は常に対称であり(距離の定義)、非対称は距離モデルにおけるエラーとみなされる。MDSは対称なデータ行列で実行される。点のそれ自身への距離は常にゼロであるため、データ行列の対角要素は無視される。図1はこれらのデータを表現した(順序ありの)MDSの輪郭である。取り違え率が信号の物理的性質にシステマチックに関係していることがわかる。北西vs南東の方向は信号の長さと相関があり、北西の角には長い信号、南東には短い信号がある。

図1: 表2のデータをMDSしたもの。モールス信号が・－でプロットされている

垂直方向のばらつきは信号のトンとツーの構成に関係しており、上方向ではツーが支配的になる。こうして、MDSは2つの心理的ルールを発見できた。もし不可能でないとしてもそれを数値データから見分けることは難しい。

この例では、MDSが基本的に、可能な限り非類似度がオブジェクトを表す点間の距離になるように、非類似度行列を低次元の地図に変換することを示した。

2. MDSのモチベーション：歴史的説明

MDSを作ったのは統計学者ではない。実践的科学の文脈で、あるスケーリングの問題を解くために開発されたものである。

2.1. 地理における初期のMDS

MDSの最初の痕跡は17世紀に見られる。図2はイングランド、ダラム群のいくつかの村と町の間の距離を示す表である。

図2: 1635年、Jacob van Langrenによるダラム群の地図

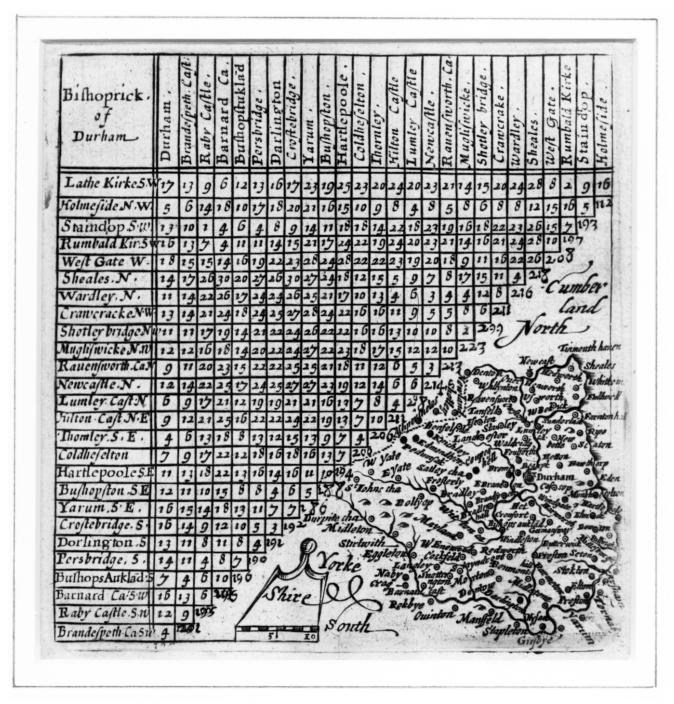
行と列で町名が逆順になっているので左下-右上の対角に関して対称という見慣れない距離行列になっている。この行列は自分の町自身への距離0は含まず、ロンドンへの距離というものを含んでいる。この表とは別に図2はダラム群の地図が描かれている。これは距離行列とそれに対応する地図を一つの図に示した最初の例だと考えられる(Gower, 個人的な会話による)。従ってこれはMDSの先駆であるとみなせる(この地図はイングランドの群をカバーしたシリーズの内の一つである。ドイツの地図製作者Jacob van Langrenにより1635に作成された。)。
近代的なMDSは地図とは関係ない。むしろ要素分析(factor analysis)に近く、特定の心理現象のモデルとして進化し、のちになって一般のデータ解析ツールとして人気になっただけである。MDSは歴史的に最低4つの目的と関連する。

2.2. （非）類似度判断の心理モデルとしての距離の式

（非）類似度判断は距離としてモデル化できるという考えは、心理学において長い間存在してきた。デカルト座標空間での自然な距離関数を模倣したプロセスで、人々がオブジェクトペアの（非）類似度判断を行うのは自明なことに思える。つまり、判断が必要なとき、人はオブジェクトの属性によって張られ、オブジェクトがその座標系での点に対応するような”心理的空間”にオブジェクトの精神的な表現を形成する。非類似度の判定はその後、最初に各点のペアの違いを次元ごとに評価し、それから次元間の差を足すことで形成される。このことは、全体の非類似度の印象のベースや各オブジェクトの評価となるグローバルな距離を作り出す。人は物体たちの属性を元に頭の中でそれらを空間にマッピングしている。それが似ている・似ていないの判断の元になる
観測者にとっては、（本人もかもしれないが）、心理的空間自体は未知(潜在的)である。しかしMDSのパイオニアであるKruskalが主張しているように、MDSは個人の（非）類似度の判断を元にその空間を"明らか"にできる。このために、古典的なMDSは、与えられた判断はメトリックスケール(metric scale)でのレーティング(評価)であり、心理空間での距離関数はユークリッド距離であると仮定している。metric scale：日本語約は不明だが、変数の性質を説明する尺度。頻度、順位を決定でき、平均を計算できる。代表例にセルシウス温度がある。セルシウス温度はある温度より高いか低いかが明らかにわかり、10℃と20℃の間は30℃と40℃の間と同じ間隔がある。また平均が意味を持つ。（１か月の平均気温など）こちらを参考にした。

しかしこの距離モデルが注目を集める前に、metricではなく順序データ(ordinal scale)を処理できるものは、MDSアルゴリズム以前には存在しなかった。これが順序データ(ordinal scale)を重要視した60年代の時代精神に合っていた。ordinal scaleはmetric scale より「弱い」尺度だと考えられる。順序なので例えば平均が計算できない。つまりordinalの方ができることが限られる（metric scaleはordinalも含んでいた）
のちにユークリッド距離の公式はより一般的なミンコフスキー計量(Minkowski metric)に一般化される。Minkowski metricは理解できていない。・・・でもどうやらここで言うのはミンコフスキー距離のことらしい。ミンコフスキー距離はユークリッド距離の一般化。以降Minkowski metricがミンコフスキー距離と思われるときはミンコフスキー距離と記載する
この計量は次元内の距離が、加算される前に、その絶対的な大きさに比例して重みづけられる距離の族である。ミンコフスキー距離は全ての次元内の違いが重み１であるもの(マンハッタン距離)から、最も異なるものが基本的に総和と等しくなるような極端な重み(dominance metric)(おそらくチェビシェフ距離（最も違いの大きい次元の距離が全体の距離になる）のこと)まで変化する。どの文脈でどのミンコフスキー距離が適しているのか一連の研究が行われた。ミンコフスキー空間がlocal validityを持つのは（非）類似度の判断が劣化法的(subadditive)だからではないかということが議論された。劣化法性：$f(x+y) \leq f(x) + f(y) (\forall{x,y \in A})$がなりたつ
この経験的なルールの説明のために、Sch¨onemannはある有界な幾何学とMDSモデルを提案した。しかしこのアイデアは心理学研究では基本的に無視され、精神測定医によってさらに追及されることはなかった。

そのような距離モデルによって説明される類似度の修正とともに、MDSにおける個人のち外をモデリングするためにattentionが投入された。これは非常に人気のあるモデルを生み出した。そのモデルはよく、Indscalと呼ばれる特定のプログラムとして認知されている。このモデルは個人が異なるのは、共通する空間での同一の次元の集合をどのように重み付けるかということにおいてである、と仮定している。（空間内の次元の集合という同じものを見ても、別の人が見れば重みの付け方が異なる）
”その”次元をユニークに特定できるので、社会科学における非常に多くの応用がこのモデルを使用した。グループ空間の回転によってデータの説明があまりうまくいかなくなることがPINDISのようなステップ・バイ・ステップのアプローチにより示されるまでは。さらに、(attentionの)個別の次元の重みは、重み１よりもはるかに多くの分散を説明なく散らばらせるという意味で、不明瞭である。各軸に重みが散らばりすぎて、どの軸が重要なのかわからなくなるということ？
しかし、INDSCALモデリングを使うときの一番のミスは、個別の重みの比較があまりにもゆるいということだ。これらの重みは、同じ次元に関する異なる人の重みの順番だけが比較されるように、グループ空間の(任意の)normingに依存する。norming
一方でマーケットリサーチャーはINDSCALがプロダクトの認知においてどの次元が最も重要なのかを示してくれることを望んでいたのに。重みの大きさそのものには意味がなく、ある軸が次元全体でどのくらいの割合の重みを持っているかが示される、ならばマーケットリサーチャーの希望は満たせる。それよりもっとゆるい？
これらの制約が明らかになると、INDSCALは応用研究であまり重要ではなくなった。

MDSを使ったさらなる研究には、Coombs’ unfolding model,(Coombs 1964)を解くためのものがあるが、データが（非）類似度ではなく、同じ物体のセットに関する個人の好みであった。unfoldingにおいて、人は空間の点として表現され、物体のチョイスは別の点である。これらの２種類の点の間の距離は好みを表す。各人の点は、この人の好みが最大の点("理想の点")として見なせる。また各理想の点を中心とする円は好みが等しい(iso-preference)輪郭である。
unfoldingは例えば投票行動をモデリングするのによく使われた。しかし、理論に基づいた、異なるサブグループについての複数の、単一次元のunfoldingは、探索的にサンプル全体の多次元unfoldingするよりも優れていることがわかった。サンプル(複数の物体)をサブグループ(一つずつ)に分けて、１次元で好みを判定して１物体ずつプロットしていく、と解釈した。そしてそのような簡単なモデルのほうが性能が良かった。
よって、unfoldingの好みモデルとしての人気は下降した。
MDSの幾何とその距離関数を心理学モデルとして捉えるこのような研究は人間の認知や判断、好みにたいする理解を大いに進展させた。特に、そのようなモデルが、どのような条件のもとでなら経験的な現象をうまく説明できるのかということが明らかになった。今日では、一般的なMDSが心理学モデルとして主要な役割を果たす研究は終りを迎えている。

2.3. 「心理学における測定は非数値データに基づいているべき」という前提に答える順序MDS

60年代末、方法論の研究者はFoundations of Measurement” (Krantz et al., 1971)に関心を持っていた。この研究構想の重要な前提は数値的な判断(ほとんどの場合0から10までのスケールで「評価」される)は実数であることを自動的には仮定できないものであった。むしろ実数による測定を構築するべきであり、まずは、いくつかの技術的な仮定により、”関係のマップを保持した構造をnumerical systems(ホモモルフィズム)に確立するような、ペアごとの順序判断の大規模な集合”をテストして正しさを示すことを主張していた。0-10の評価は各数値の間（1〜2の間等）が連続ではないので、これを連続値にできるようにする。
ホモモルフィズムは写像した先の空間でも写像前の関係が保持される写像。$f(xy)=f(x)f(y)$が満たされる。
実数による順序評価を使って、「２つの物体のどちらが順位が上か」のような調査データを作り、その評価結果の関係がモデルで処理した後も変わらないようなモデルを作りたい、という意味だろうか?
この計測哲学に応えて、方法論研究者は入力としてメトリックなデータを仮定していた古典的MDSを順序(ordinal)MDSまたは非メトリックMDSとよばれたものへ置き換える方向へ動いた。

KruskalとGuttman は(Lingoesとともに)順序MDSのプログラムを開発した。２人とも点座標を最適化するのに勾配ベースの最小化を使ったが、Kruskalは距離上でのデータの順序回帰(ordinal regression)と組み合わせ、Guttmanはターゲットとして"rank images"を発明した。この方法はdegenerate solutionsになりにくい。degenerate solutions
その他の技術的な違いもあるが(後に両方の長所をもつMINISSAというプログラムに統合された)、最大の違いはどのようにMDSの解に到達したかということだ。Kruskal（当時MDSを最も利用していた）は”次元は何を意味するか”を考え、Guttmanは対照的にコンテントドリブンだった。彼にとってコンテントが最初に来て、手法はデータとのパートナーシップにおける実質的な理論を構築するための道具として役立っただけだった。彼はMDSを”SSA”（Smallest Space Analysis, 後にSimilarity Structure Analysisと解釈された）と呼んだが、これは彼がMDSのデカルト座標（Cartesian dimensions）表現が、幾何学的な問題を解くための代数的な足場であることを強調したかったためである。ゆえに、その物体(MDSで分析している物体？)に関する実質的な知識に対応するいかなる幾何学的パターン（次元、方向、クラスタ、図、そして特に領域と近傍のような）も意味がある。この視点は後にfacet theoryに発展し、partial order scalogram analysisのような別のデータ解析法につながる。facet(切子面)は、例えば四面体をカットした断面にできる三角形のようなもの(参考)
順序MDSは多くの応用を刺激したが、利用という意味では長年に渡り、区間MDSと比率MDSの利用がかなり回復した。これは一方では統計的な理由があり（区間MDSの解は、例えば、タイトな点クラスタが少なく雑然としていない）、もう一方には理論的な理由があった（計測法確立の強調は、ほとんど終わりのないシングルデータセットのテストから離れて、累積的な理論構築へとシフトしていた。(先述のFoundations of Measurement” (Krantz et al., 1971）の最初の主張から離れた)そして、メトリックMDSの解は”オーバーフィット”した順序解よりもシンプルでよりロバストな解釈を可能にした）。今日では順序MDSはいくつかのMDSモデルの一つである。高度なプログラムはそれらの解を数秒で生成できるので、解はほとんどコストなしにテストできる。

2.4. 学習におけるgeneralization gradientsの形状を研究する手段としての順序MDS

MDSの歴史的なモチベーションは学習の心理学におけるある問題と密接にリンクしている。その主なフォーカスはMDSの空間そのものではなく、それらが表すデータに対するMDSの距離の回帰関数の形である。この関心を生み出す理論は次のとおり。もし反応$R$が刺激$S$に条件付けられているなら、$S$に似た刺激も、ある確率で反応$R$を引き起こす傾向にある。この確率は$S$と$S'$の距離についての単調減少な関数であるはずである。しかし$S$と$S'$は物理空間ではなく認知的な空間にあるので、generalization gradientの形状を判断することは難しい。ここでgeneralization gradientは心理学用語。generalization(訓練中には無かった刺激によって訓練中に学習した行動が現れること、例：アルバート坊や）を記録したもの（グラフ）を指すらしい。(参考)
しかし、刺激と刺激$S_k$に対する反応$S_i$が現れる確率の測定を与えることで、この問題はMDSの問題になる：データが類似度として測定されているなら、最初にそれらを順序MDSでスケールする。そしてMDSの距離のデータへの回帰のトレンドがgeneralization gradientの形状を示す。したがってShepardは、gradientが指数減衰または線形減衰する関数であると仮定するより、データ自身に喋らせたいと考え、generalization gradientが経験的に、今日”Shepard図"として知られているものを通ることを発見した。Sheardは実際に問題を解くことはできず、その問題に苦しんだが、Kruskalに順序MDSのアルゴリズム（M-D-SCAL）をスケーリングタスクに対する統計学者の回答として開発させる動機を与えた。
shepard図

今日、Shepard図が主要な関心になっているMDSの応用は極めて珍しい。むしろ研究者はほとんどいつもMDSの空間そのものまたは、その空間で表現されたオブジェクトの既知の、または推定される性質との関係にフォーカスしている。順序MDSは特定のモデルの推定を経験的にチェックするのに役立つ。例えばThurstonian Case-5 scalingにおいて、支配的な確率は累積的なガウス関数によってスケールの差にマップされる。Thurstonian Case-5 scaling
そのようなマッピング関数を仮定しなくとも、順序MDSを使ってデータをスケール距離(scale distances)にスケールできるし、マッピング関数が実際にS-shapedかどうかを経験的にチェックできる。s-shaped:シグモイド関数みたいな形のこと？

2.5. 一般的なデータ解析ツールとしてのMDS

順序MDSが可能になると、心理学以外の領域、特にマーケットリサーチャーに熱狂的に迎えられた。Greenとその同僚は、消費者がどのように製品を認知するかを”明らかにする”ためにMDSを使う方法を示した本と論文のスコアを発表した。社会学者も社会ネットワーク、特に態度と価値を研究するためにMDSを利用した。例えばSchwartzは、今日でも利用される社会的価値に関する影響力のある理論であるTheory of Universals in Values (TUV)を作るために利用した。TUVは２次元MDS空間における領域のcircumplex（地域セクションの輪）に密接な関係がある。circumplexは対人行動を評価する円環グラフ。たぶんレーダーチャートみたいなもの
TUVはMDS空間を同じカテゴリの値(例えば達成感、セキュリティ、楽しさなどを表す値)を表す点だけを含む近傍に分割する。一方GreenはMDSを真に探索的な方法で使い、Schwartzは(Guttman同様)コンテントドリブンであり、ゆえにMDSオブジェクトとその空間における表現についてのコンテント理論の対応を探した。
しかしSchwartzはそのような外部的な制約をconfirmatory MDS(CMDS)を使ってMDSの解に強制したりしなかった。CMDSは８０年台初期から存在したが。DeLeeuwやHeiserは特定の形のCMDSを開発しており、PROXSCAL(統計パッケージSPSS)やSMACOF(R言語)はそれらの多くを扱うことができる。しかし、MDSの設定に対する多くの外部制約は（次元数を除き）現在のMDSプログラムでは設定することが難しい（または不可能である）。またこの制約の影響を統計的にどのように評価するのかが明確でない。時々現在のプログラムは誤った解を出力するが、応用研究者がこの原因を分析することは難しいことがある。実質的な研究者の観点からは、これはもっと多くの研究が必要とされており、近年ではCMDSの研究は注目を浴びている。

別のラインの研究としては、距離モデルに対する一般的な争点を扱ったものがある。つまり、距離は常に対象であるが、(非)類似度データは対象とは限らないということをである。非対称データの扱いに関していろいろな提案がなされた。ほとんどは最初にデータの情報を対称部分(MDSでモデリングできる)とゆがんだ対称(skew-symmetric)部分（これは例えばベクトル場につながる小さい矢印として、MDS空間の点に加算できる）に分けるものである。このモデルはどのように人が非対称な(非)類似度を作り出すのかを説明するという意味で心理学モデルではない。(説明できていない。)
むしろこれらは非対称な(非)類似度データにおけるシステマチックなトレンドを示す便利な統計的ツールである。しかし、これらのモデルに関してユーザフレンドリーなプログラムは今の所存在せず、ゆえにこれらの手法の統計的診断についてのポテンシャルはまだ利用されていない。

2.6. 今日のMDSの利用

今日、MDSの開発につながったモチベーションの多くは重要ではなくなった。生き残ったものはGuttmanの意味でMDSを使っており、具体的には、態度と価値の研究である。そこではアイテムの概念的facetsとその空間的表現の領域との対応に関して、調査対象アイテムの相互相関が研究されている。どのようなアイテムが同じような空間表現になるかを研究している？
しかし多くのMDSの応用は今日もっと広い目的に利用されている。すなわち、（非）類似度データとみなせる表を可視化するために。その目的では、

MDSはそれが（非）類似度(相関、共分散、共起、プロファイル距離)である限り非常に広範囲なデータを扱えるのでとても便利である。
さらにinterval-scaledなデータでなくとも順序データでも(さらに名義的データ(nomaial)でも)よい。
データ抜けや粗い(coarse)データに対してロバストである。高いエラー条件のもとでさえ複製可能な構造を示すデータスムーザーとしても使える。(？)
専門家以外にも説明しやすく、解を探索してもリスクが少ない（ユークリッド計量を使う限り）。
アルゴリズムは割と難しいが、専門家以外でも実行しやすい（車の運転はエンジンの動作を知らなくてもできる）。
ユーザに特定の解釈(特に”次元数”)を押し付けない。データが自分から話せるようにする。

２章終わり

MDSの現在・過去・未来

本文

概要