やりたいこと
Googleスプレッドシートでは入力した数値からグラフを作成し、グラフを近似する曲線と方程式を描画できる。
しかし、この方程式はテキストとしてコピーできない。(2019/1/25時点の筆者調べ。)
不便なのでGASを使って、セルの数値からグラフを対数近似する関数を計算し、表示されている方程式と同じものをテキストとしてセルに出力するコードを書いた。
問題設定
こんな感じになっているとする。
xの列はグラフの横軸、yの列はグラフの縦軸に対応する。
入力xとそれに対する出力yの組が5個あるというデータ。
このデータの関係を表現する式を導出したい。
（右のグラフにはすでにgoogleが計算してくれた式が出ている。これをテキストで欲しい。）
ちなみに、xの最小値が1になっているのは、今回作成したコードではxに0が来るとlog(0)を計算し、結果がNanになるため。まだ対策できていない。
（今年初めまでのSpread Sheetではgoogleの計算も0を回避していた(データ点そのものが無視された)記憶があるんだけど、今は普通に計算されている。↓の画像参照。）
xに0を入力した場合。googleは計算でき、結果が上の画像と違う。今の筆者のコードではできない。
解き方
1. 最小二乗法を使う
このベストアンサーをコードに起こした。
リンク先の説明を拝借しながら説明すると、
$y=a\ln x+b$ が当てはめるべき式。
$X=\ln x$として、
$y_1, X_1$
$y_2, X_2$
$\vdots$
$y_n, X_n$
の値の組を得る。つまりこれらの組はそれぞれ、
$y_1=aX_1+b$
$y_2=aX_2+b$
$\vdots$
$y_n=aX_n+b$
という関係。
最小二乗の原理から
E=\sum_{i=1}^{n} ( aX_i+b-y_i )^2 \tag{1}
を最小にするa, bを求めればよいので、
$(1)$をaで偏微分して0とおき
\begin{align}
\frac{\partial E}{\partial a}=\sum_{i=1}^n 2 X_i (a X_i+b-y_i)&=0 \\
a\sum_{i=1}^n X_i^2+b\sum_{i=1}^nX_i&=\sum_{i=1}^nX_iy_i \tag{2}
\end{align}
同様にbに関して
\begin{align}
\frac{\partial E}{\partial b}=\sum_{i=1}^n 2 (a X_i+b-y_i)&=0 \\
a\sum_{i=1}^n X_i+n b &=\sum_{i=1}^n y_i \tag{3}
\end{align}
が得られる。
$(2)$$(3)$は正規方程式といい、連立させて解けばa,bが得られる。
元記事の回答執筆者candy712様、ありがとうございます。
2. 逆行列で連立方程式を解く
上記$(2)$$(3)$を眺めてみると、
\begin{align}
a\sum_{i=1}^n X_i^2+b\sum_{i=1}^nX_i&=\sum_{i=1}^nX_iy_i \tag{2} \\
a\sum_{i=1}^n X_i+n b &=\sum_{i=1}^n y_i \tag{3}
\end{align}
\begin{align}
a(何かスカラー)+b(何かスカラー)&=(何かスカラー) \tag{2} \\
a(何かスカラー)+(何かスカラー)b &=(何かスカラー) \tag{3}
\end{align}
という形をしている。
つまり、２行２列の行列$A$と、a,bをまとめたベクトル$x$の積、および右辺の２個のスカラーをまとめたベクトル$c$の関係として
Ax=c
のように書ける。
(xが何回も出てきて紛らわしいが)$x$の中身であるa,bを求めたいので、$A$の逆行列$A^{-1}$(存在すると仮定する)を用いて、
\begin{align}
A^{-1}Ax&=A^{-1}c \\
x&=c'
\end{align}
$c'$は$A^{-1}c$を置き換えたもので、2要素のベクトルとなる。もともと
x=
\begin{pmatrix}
a \\
b
\end{pmatrix}
であったので、これでa,bが求められた。
コード
逆行列を計算する関数はt.hira様のJavaScript で逆行列と行列式の値を求めるからお借りした。掃き出し法を使用されている。
また、少数第一位で四捨五入する関数を@nagito25様の【JavaScript】桁指定して四捨五入・切り上げ・切り捨てからお借りした。
ありがとうございます。この場を借りてお礼申し上げます。
function appx_log(){
//sheet名を指定
var ss = SpreadsheetApp.getActive().getSheetByName('log_approx');
//47行3列目から５行分取得
var r_range=47;
var c_range=3;
var get_range=5;
var range = ss.getRange(r_range,c_range,get_range);
var values=range.getValues();
var NUM_POINTS=5; // データ点数が5個
var xs=[1, 50, 100, 150, 200]; //横軸(x軸)の値
var Xs = [];
var ys=[];
var sum_ys=0;
var sum_Xs=0;
var sum_Xsys=0;
var sum_sq_Xs=0;
//yの配列とyの和を準備
for(var row in values){
for(var col in values[row]){
var val=values[row][col];
Logger.log(val);
ys.push(val);
sum_ys+=val;
}
}
//Xの配列とXの和、Xの2乗の和、Xとyの積の和を準備
for (var i =0; i<xs.length; i++){
var val=Math.log(xs[i]);
Logger.log(val);
Xs.push(val);
sum_Xs+=val;
sum_sq_Xs+=Math.pow(val,2);
sum_Xsys+=val*ys[i];
}
//係数行列Aとその逆行列を作る
var A=[];
var order=2;
for (var i=0; i<order; i++){
A[i]=new Array(order);
}
A[0][0]=sum_sq_Xs;
A[0][1]=sum_Xs;
A[1][0]=sum_Xs;
A[1][1]=NUM_POINTS;
var inv=inverse(A);
//a, bを計算する
var a=inv[0][0]*sum_Xsys+inv[0][1]*sum_ys;
var b=inv[1][0]*sum_Xsys+inv[1][1]*sum_ys;
a=orgRound(a,10);
b=orgRound(b,10);
//"10+-20.5lnx"のような変な表記を回避
var ret;
if(a<0){
ret=String(b)+ String(a)+"lnx";
}else{
ret=String(b)+"+"+ String(a)+"lnx";
}
Logger.log("result:%s", ret);
//取得した５個のデータの下のセルに出力
ss.getRange(r_range+get_range,c_range).setValue(ret);
}
//http://thira.plavox.info/inverse/
function inverse(a){
var c=a.length; //行列の次数
var buf; //一時的なデータを蓄える
var i,j,k; //カウンタ
//単位行列を作る
var inv=new Array(c);
for(i=0;i<c;i++){
inv[i]=new Array(c);
for(j=0;j<c;j++){
inv[i][j]=(i==j)?1.0:0.0;
}
}
//掃き出し法
for(i=0;i<c;i++){
buf=1/a[i][i];
for(j=0;j<c;j++){
a[i][j]*=buf;
inv[i][j]*=buf;
}
for(j=0;j<c;j++){
if(i!=j){
buf=a[j][i];
for(k=0;k<c;k++){
a[j][k]-=a[i][k]*buf;
inv[j][k]-=inv[i][k]*buf;
}
}
}
}
return inv;
}
//https://qiita.com/nagito25/items/0293bc317067d9e6c560
function orgRound(value, base) {
return Math.round(value * base) / base;
}
実行
[ツール]->[スクリプトエディタ]からGASのエディタを開く。
実行する関数（右の丸）を選択し、実行ボタン(左の丸)を押す。
ちなみに
[表示]->[ログ]からLogger.log()で出力させたログが見れる。
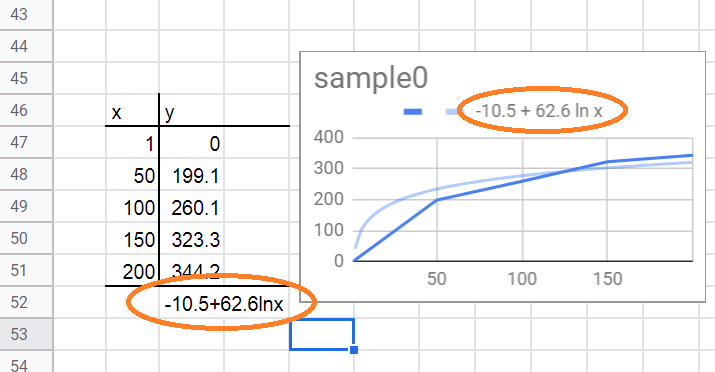方程式がセルに出力され、googleの計算結果と一致している。
まとめ
- 方程式をテキストで得るために、GASで対数近似を計算するスクリプトを書いた。
- 最小二乗法と逆行列による解法を使用した。
- 現時点ではxに0が含まれる場合は計算できない
展望
- xに0が含まれる場合に対応すること
- べき級数近似も欲しい。$y=ax^{b}$へのあてはめを目的に非線形最小二乗法を使う気がしている。(全然違うかもしれない)
- 今回の$X=\ln x$とおいて$y=aX+b$で計算するというのは、カーネル法的な考え方なんじゃないか。(全然違うかもしれない)
なお、筆者はjavascriptの文法を知らない。GASは今回初めて使用した。数学も素人なので、突っ込みなどお待ちしています。