Wasserstein GANの要約とメモ

2022/02/22追記:

「GANディープラーニング実装ハンドブック」 https://www.amazon.co.jp/dp/4798062294 という書籍の付録B,CにWasserstein GANの解説を書きました．執筆当時では日本語の解説としてはかなり詳しく書いたつもりです(2021/02/13 発売)が，数学的に厳密ではありません．それぞれ以下のような内容を説明しています．

• Appendix B GANの学習を説明する理論
  • GANの目的関数がJSダイバージェンスに対応していること
  • 低次元多様体とは
  • データ分布の台が低次元多様体に乗っている場合はGANの学習が停滞すること
• Appendix C Wasserstein DistanceとGANへの適用
  • ブロック移動の例を用いたWasserstein距離の直感的な説明
  • リプシッツ連続性
  • Wasserstein距離やその他のダイバージェンスが連続になるかどうか
  • Wasserstein GANでのWasserstein距離の利用
  • gradient penalty(WGAN-GP)の解説

追記ここまで

---

**Wasserstein GAN(Arjovsky et. al. 2017)**の要約とメモ。
筆者の理解と疑問を青色でメモしている。
本論文は付録に各証明があるが、この記事には含まない。

従来のGANの訓練で誤差関数に用いられるJSダイバージェンス等の距離が、通常の(低次元多様体でサポートされた)データでは機能せず、EM距離(Wasserstein距離)では問題を回避できることを示す。
EM距離の計算コスト回避のため近似するが、これにリプシッツ制約が必要となる。この制約を満たすためにモデルの重みパラメータをある区間にクリッピングする。
この手法で訓練したDは最適まで一気に訓練でき、Gはモードコラプスが発生しない。G,Dのアーキテクチャは任意に変更可能。

6. 結論

従来のGAN訓練の置き換えであるWGANを導入した。このモデルは学習の安定性を改善し、モードコラプスのような問題を排除し、意味のある学習曲線を提供する。さらに、対応する最適化問題が健全であり、他の分布間の距離との深い接続に焦点を当てた幅広い理論的な解析を提供した。

1. イントロ

教師なし学習について、主に、確率分布を学習するとはどういう意味なのか？について考える。古典的な解答は「確率密度を学習する」である。よくあるのが、密度のパラメトリックファミリー $(P_{\theta})_{\theta \in
\mathbb{R^d}}$を定義してデータ上で尤度を最大化することで達成できる。

パラメトリックファミリー：その族（関連するオブジェクトの集合）内の差異が、選択されたパラメータの集合によってのみ異なるような族のこと。つまりパラメータによってのみ値の変わる$P_{\theta}$というものをつくってその尤度最大化する

つまり、実数データ

\bigl \{ x^{(i)} \bigr \}_{i=1}^m

があったとして、次の問題を解きたい。

\underset{\theta \in \mathbb{R}^d}{max} \frac{1}{m}\Sigma_{i=1}^{m} log 
 P_{\theta}\bigl(x^{(i)} \bigr)

本物データ分布$\mathbb{P}_{r}$がある密度を持ち(admits)、$\mathbb{P}_{\theta}$がパラメタライズされた密度$P_{\theta}$ならば、漸近的に、これはKullback-Leibler divergence $KL(\mathbb{P}_{r}\parallel \mathbb{P}_{\theta})$を最小化することに相当する。$P_{\theta}$が最大になるように$\theta$を変更すると、$\mathbb{P}_{r}$と$\mathbb{P}_{\theta}$という２つの分布を近づけていることに相当する。

このためには、モデル密度である$P_{\theta}$が存在することが必要。これは低次元多様体でサポートされた分布を扱っている通常の状況では起こらない。低次元多様体でサポートされた、というのは例えば画像データセットの分布のように何万次元も使わなくても、もっと少ない次元数で各データの関係を表現できるという意味。PCA等で低次元空間にうまく写像できるデータというようなイメージ。
そういう普通のデータでは、モデル密度$P_{\theta}$というのは存在しない。

その場合、モデルの多様体と真の分布の台が無視できないintersectionを持っていることは起こりそうにないし([1])、KLダイバージェンスは定義できない(または無限になる)。

その場合、データの低次元の台とモデルの多様体とが重なることはなく、分布間の距離は測れない、と言っている。
モデル密度$P_{\theta}$がないのでモデル多様体がない、ということだろうか。なぜ低次元多様体のデータだとモデル多様体がなくなるんだろう。

典型的な対策はモデル分布にノイズ項を加えることだ。古典的機械学習の文献で説明される生成モデルがすべてノイズ要素を含んでいるのはこのため。簡単なケースでは、すべてのexamplesをカバーするために比較的高いbandwidthのガウシアンノイズを仮定する。例えば画像生成もでるでは、そのノイズがサンプルの質を落とし、ぼやけた感じにすることはよく知られている。

例えば最近の論文[23]では、尤度最大化する時にモデルに加えるノイズの最適なノイズの標準偏差は、生成された画像の各ピクセルごとにおよそ0.1とされている。これはピクセルの値がすでに[0,1]に正規化されているときである。これは大量のノイズであり、彼らがサンプル生成する際には、尤度値を報告した時のそのノイズ項を加えなかった。つまり加えるノイズ項は明らかにその問題に不適切だったのだが、最尤法でやるためには必要だった。

存在しないかもしれない$\mathbb{P}_r$の密度を推定するより、固定分布$p(z)$とランダム変数Zを定義して、それをある分布$\mathbb{P}_{\theta}$に従うサンプルを直接生成するパラメトリック関数$g_{\theta}:Z \rightarrow X$(ニューラルネットであることが多い)に渡すことができる。$\theta$の値を変えることでこの分布を変更して、真のデータ分布$\mathbb{P}_r$に近づける。利点が２つある。

• 密度とはことなり、低次元多様体に閉じ込められた分布を表現できる。
• 簡単にサンプルを生成できるという能力が密度の数値を知るよりも便利(入力画像->出力画像、という条件付き分布における超解像やシマンテックセグメンテーションなど)。

一般に、任意の高次元の密度からサンプルを生成するのは困難[16]。

VAEs[9]とGANs[4]はこのタイプ。VAEsは訓練例の尤度の近似にフォーカスしており、標準モデルでの限界が適用され、追加のノイズ項が必要。GANsは目的関数の定義が柔軟である(Jensen-Shannon[4], すべてのf-divergences[17], エキゾチックな組合わせ[6])が、[1]で理論的に調査されている理由により訓練がデリケートで不安定。

本論文では、モデル分布と真の分布の近さを測る、あるいは同じことだが、距離またはダイバージェンス $\rho(\mathbb{P}_{\theta},\mathbb{P}_{r},)$を定義する、色々な方法に注意を向ける。そのような距離たちの最も基本的な差は、確率分布の系列の収束に与えるインパクトである。分布$(\mathbb{P}_{t})_{t \in \mathbb{N}}$は$\rho(\mathbb{P}_{t},\mathbb{P}_{\infty},)$が0になるような分布$\mathbb{P}_{\infty}$が存在する時、その時に限り収束し、それは距離$\rho$がどのように定義されるかに依存する。ざっくりいうと、距離$\rho$は、$\rho$が分布の系列の収束を簡単にするときには、**弱位相(weaker topology)**を誘発する。
より厳密には、$\rho$により引き起こされた位相が$\rho'$によるものより弱いのは、$\rho$の下での収束系列の集合が$\rho'$の下での集合のスーパーセットであるときである。$\rho'$での収束系列の集合は$\rho$の集合のサブセットになっている。そういう意味で$\rho'$のほうがより厳格な感じがする。
よく使う距離がその観点でどう異なるのかを2章で明らかにする。
弱位相：

パラメータ$\theta$を最適化するためには、当然モデル分布$\mathbb{P}_{\theta}$を関数$\theta \mapsto \mathbb{P}_{\theta}$が
連続になるように定義すべきである。連続性はパラメータの系列$\theta_t$が$\theta$に収束するときには分布$\mathbb{P}_{\theta_t}$も$\mathbb{P}_{\theta}$に収束することを意味する。 しかし、分布$\mathbb{P}_{\theta_t}$の収束は分布間の距離を計算する方法に依存するということを覚えておく必要がある。距離が弱い(weaker)ほど、分布が収束しやすいので、$\theta$空間から$\mathbb{P}_{\theta}$空間への連続な写像を定義するのは簡単になる。学習が簡単になる。距離が弱い＝厳密じゃない？

写像$\theta \mapsto \mathbb{P}_{\theta}$が連続であることを気にする理由は主に次のこと。$\rho$が２つの分布間の距離で、連続な誤差関数$\theta \mapsto \rho(\mathbb{P}_{\theta},\mathbb{P}_{r})$がほしい。これは分布間の距離$\rho$を使った時に写像$\theta \mapsto \mathbb{P}_{\theta}$が連続であることと等価である。$\theta$の最適化のために$\theta$を引数にとる連続な誤差関数がほしい。現在のモデルの分布$\mathbb{P}_{\theta}$は引数に取った$\theta$から計算し、真の分布$\mathbb{P}_{r}$は$\theta$については定数なので、誤差関数が連続であるためには$\theta \mapsto \mathbb{P}_{\theta}$が連続ならOK、という感じだろうか。

本論文の貢献は

• 2章で、分布の学習でよく使う確率の距離とダイバージェンスと比較して、Earth Mover(EM)距離がどのように振る舞うかについて包括的な理論的な解析を示す。

• 3章で、EM距離の効率的で妥当な近似を最小化するWasserstein-GANを定義し、対応する最適化問題が理論的に健全(sound)であることを示す。健全性：前提が真ならば、結論が必ず真(=(演繹的に)妥当)であり、かつ前提が全て真であること。つまり、前提が真ならば結論が真であり、前提が真であること

• 4章で、WGANがGAN訓練の主要な問題を解決することを示す。特に、DとGのバランスを慎重に維持する必要がなく、ネットワーク構造の慎重な設計もいらない。mode droppingも劇的に減少する。WGANの最も説得力ある利点はDを最適まで訓練することでEM距離を連続して推定できることである。これらの学習カーブのプロットはデバッグやパラメータサーチに便利なだけでなく、驚くほど生成サンプルの品質と関連する。Dを最適まで訓練して、その後Gの訓練をしても大丈夫というはなしだったはず。また、誤差関数値の良さとサンプル品質が一致しないというのが従来の問題だった。

異なる距離

記法を定める。$\chi$をコンパクトな計量の集合($[0,1]^d$の画像の空間など)とし、$\chi$のすべてのボレル部分集合の集合を$\Sigma$とする。ここで２つの分布$\mathbb{P}_r,\mathbb{P}_g \in Prob(\chi)$の間の基本的な距離とダイバージェンスを定義できる：
ボレル集合:
計量:

• Total Variation (TV) 距離

\delta(\mathbb{P}_r,\mathbb{P}_g)= \underset{A \in \Sigma}{sup} |\mathbb{P}_r(A),\mathbb{P}_g(A)|
```

• Kullback-Leibler (KL) divergence

KL(\mathbb{P}_r \parallel \mathbb{P}_g) = \int log \Bigl(\frac{P_r(x)}{P_g(x)}\Bigr)P_r(x)d\mu(x)

```

ここで$\mathbb{P}_r $と$\mathbb{P}_g$は共に絶対連続であるため、$\chi$上で定義された同じ測度(measure)$\mu$について密度が認められる。

関数の絶対連続：
ある区間の部分区間幅の有限列の和がある正の数$\delta$で抑えられるとき、その区間幅たちの両端の値に関数fを適用した新たな区間幅の系列の和が、ある数$\epsilon$で抑えられる、というような感じ。
測度の絶対連続：
同じ可測空間上の2つの測度 μ と ν について、μ(A) = 0 となる可測集合が必ず ν(A) = 0 を満たすとき ν は μ に関して絶対連続であるといい、ν ≪ μ と書く。
測度：
面積、体積、個数といった「大きさ」に関する概念を精緻化・一般化したもの。

なお、確率分布$\mathbb{P}\_r \in Prob(\chi)$が$\mu$に関して密度$p\_r(x)$を認める、すなわち$\forall{A} \in \Sigma, \mathbb{P}\_r (A)=\int_A P_r(x)d\mu(x)$であるのはそれが$\mu$に関して絶対連続、すなわち$\forall{A} \in \Sigma, \mu(A)=0 \Rightarrow \mathbb{P}_r(A)=0$である時に限る。

KLダイバージェンスは非対称であり、<font color="LightSteelBlue">(距離の定義のうち対称性を満たさない)</font>また、$P\_g(x)=0$かつ$P\_r(x)>0$であれば無限大になりうる。

• Jensen-Shannon(JS) divergence

  JS(\mathbb{P}_r , \mathbb{P}_g)=KL(\mathbb{P}_r \parallel \mathbb{P}_m) + KL(\mathbb{P}_g \parallel \mathbb{P}_m)
  
  

  ここで、$\mathbb{P}_m$は混合分布$\frac{\mathbb{P}_r+\mathbb{P}_g}{2}$。このダイバージェンスは対象であり、$\mu=\mathbb{P}_m$(KLの分母)を選べるので常に定義される。

• Earth-Mover(EM) 距離

  W(\mathbb{P}_r,\mathbb{P}_g)= \underset{\gamma \in \Pi{(\mathbb{P}_r,\mathbb{P}_g)}}{inf}\mathbb{E}_{(x,y)\sim\gamma}\bigl[ \parallel x-y \parallel \bigr] \tag{1}
  

  差x-yのノルムの、同時分布(x,y)に関する期待値の下限。3章の初めにこれがintractableであるされているが、同時分布について期待値をとるのが、x,yの組み合わせがありすぎる、ということだろうか。
  ここで$\Pi{(\mathbb{P}_r , \mathbb{P}_g)}$は周辺分布がそれぞれ$\mathbb{P}_r$と$\mathbb{P}_g$であるようなすべての結合分布$\gamma(x,y)$の集合。直感的には$\gamma(x,y)$は分布$\mathbb{P}_r$を分布$\mathbb{P}_g$に変形するためにxからyにどれくらいの”質点”が輸送される必要があるかを示す。EM距離はゆえに最適輸送計画の"コスト"である。

次の例はシンプルな確率分布の系列がどのようにEM距離で収束し、上記の他の距離とダイバージェンスでは収束しないかを示す。

例1 (平行線の学習)

$Z \sim U [0,1]$を単位区間の一様分布とする。$\mathbb{P}_0$を$(0,Z) \in \mathbb{R}^2$(x軸が0、y軸がランダム変数Z)の分布で、原点を通る垂直な直線上で一様分布であるとする。今、$\theta$を一つの実数のパラメータとして、$g_{\theta}(z)=(\theta, z)$とする。このケースでは次が容易にわかる。

• W(\mathbb{P}_0 , \mathbb{P}_{\theta}) = |\theta|,
  
  

• JS(\mathbb{P}_0 , \mathbb{P}_{\theta}) =   \begin{cases}
  log2 & if \theta \neq 0, \\
  0 & if \theta=0,
  \end{cases}
  

• KL(\mathbb{P}_{\theta} \parallel \mathbb{P}_0) = KL(\mathbb{P}_0 \parallel \mathbb{P}_{\theta})  \begin{cases}
  +\infty & if \theta \neq 0, \\
  0 & if \theta=0,
  \end{cases}
  

•  \delta(\mathbb{P}_0 , \mathbb{P}_{\theta}) =   \begin{cases}
   1 & if \theta \neq 0, \\
   0 & if \theta=0.
  \end{cases}
  

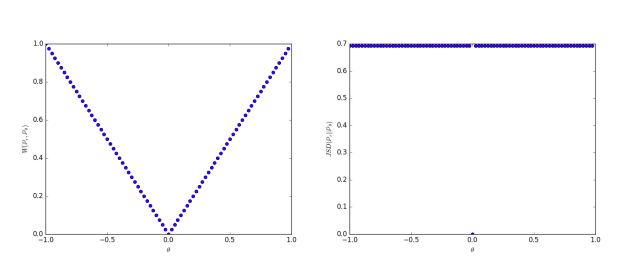
$\theta \rightarrow 0$のとき、系列$(\mathbb{P}_{\theta_t})_{t \in \mathbb{N}}$はEM距離のもとでは$\mathbb{P}_{0}$に収束するが、他では収束しない。図1はEMとJSについてこれを示している。

図1
$\rho$がEM距離(左)、またはJSダイバージェンス(右)であるときの$\theta$の関数として$\rho(\mathbb{P}_{\theta},\mathbb{P}_{0})$をプロットした。EM距離は連続であり、いたるところで利用可能な勾配を提供する。JSは不連続であり勾配を提供しない。

例１はEM距離上での勾配降下法によって低次元多様体上の確率分布を学習できるケースを示している。これは他の距離・ダイバージェンスではできず、誤差関数が不連続になるため発散する。このシンプルな例は台が重複しない(disjoint supports)分布を扱っているが、台が測度0の集合の中で空でない重なり(intersection)を保つ場合にも結論は変わらない。? 測度0の集合中で
このことは２つの低次元多様体が一般的な位置で重複するケースでも起こる[1]。つまり一般にもEM以外は学習には使えない
Wasserstein距離はJSダイバージェンスよりかなり弱いため、$W(\mathbb{P}_{r},\mathbb{P}_{\theta})$が弱い仮定(mild assumptions)のもとで$\theta$の連続な誤差関数であるのか知りたい。これが真であり、それ以上であることを示す。

定理1.

$\mathbb{P}_{r}$を$\chi$上の固定の分布とする。Zを他の空間$Z$上でのランダム変数(ガウス分布など)とする。$g:Z \times \mathbb{R}^d \rightarrow \chi$を関数とし、$g_{\theta}(z)$で表記する。$z$は座標であり、$\theta$は２番めの座標。$\mathbb{P}_{\theta}$を$g_{\theta}$(Z)の分布とすると、次が成り立つ。

1. gが$\theta$で連続ならば、$W(\mathbb{P}_{r},\mathbb{P}_{\theta})$も連続
2. もしgが局所的にリプシッツ(Lipschitz)で、regularity assumption 1を満たすならば、$W(\mathbb{P}_{r},\mathbb{P}_{\theta})$はいたるところ連続であり、ほとんどいたるところで微分可能。regularity assumption 1の意味がわからないが、well behaved なものをregularであるという説。　付録Bのassumption1のことと思われる。
3. 1,2の記述は$JS(\mathbb{P}_{r},\mathbb{P}_{\theta})$やKLにはあてはまらない。

証明

付録C参照。

系1

$\theta_g$が$\theta$でparameterizedされた任意のニューラルネット<sup>4</sup>で、$p(z)$が$\mathbb{E}_{z\sim p(z)}[\parallel z \parallel] < \infty$(例えばガウシアン、一様、など)であるz上の事前分布とする。$\parallel \cdot \parallel$は何らかのノルム
このとき仮定1(regurality assumption 1と思われる)が満たされ、ゆえに$W(\mathbb{P}_{r},\mathbb{P}_{\theta})$はいたるところで連続でほとんどいたるところで微分可能。

<sup>4</sup> フィードフォワードニューラルネットはアフィン変換となめらかなLipschitz関数であるpointwiseな非線形関数(sigmoid, thnh, elu, sftplus etc.)で構成された関数のこと。reluの場合は証明が少し異なる。

証明

付録C参照。

これらによりEMは今の問題にたいして少なくともJSより気の利いたコスト関数であることがわかる。次の定理は距離やダイバージェンスにより引き起こされる相対的なトポロジの強さを示す。強い順にKL, JS and TV, EMである。

定理2.

$\mathbb{P}$がコンパクト空間$\chi$上の分布であり、$(\mathbb{P}_n)_{n \in \mathbb{N}}$ が$\chi$ 上の分布の系列。$n \rightarrow \infty$のすべての極限を考える。極限で分布が収束するか?

1. 次に示すことは等価である
   • total variation 距離$\delta$について、$\delta(\mathbb{P}_n, \mathbb{P})\rightarrow 0$
   • JSダイバージェンスについて $JS(\mathbb{P}_n, \mathbb{P})\rightarrow 0$
2. 次に示すことは等価である
   • $W(\mathbb{P}_n, \mathbb{P})\rightarrow 0$
   • $\mathbb{P}_n \overset{D}{\rightarrow} \mathbb{P}$ ただし$\overset{D}{\rightarrow}$ はランダム変数の分布の収束を表す。
3. $KL(\mathbb{P}_n \parallel \mathbb{P})\rightarrow 0$または$KL(\mathbb{P} \parallel \mathbb{P}_n)\rightarrow 0$は(1)における記述を意味する。JSがKLから成るから。だが非対称なのに"または"でいいのか？
4. (1)の記述は(2)の記述を意味する。？

###証明
付録C参照。

これにより、KL, JS, TV距離は低次元多様体でサポートされた分布を学習するためには利口ではない。しかしEMはその状況でも気が利いている。そこで次章ではEMを最適化する実用的な近似を導入する。EMの場合は分布間の距離=0がランダム変数の分布が一致していることに対応する。他の距離では分布が一致しなくても距離0になるということ？？あとで証明を見る

3. Wasserstein GAN

定理２は$W(\mathbb{P}_r , \mathbb{P}_\theta)$が最適化したときに$JS(\mathbb{P}_r , \mathbb{P}_\theta)$よりも良い性質を持っていることを示した。しかし式(1)の下限(infimum)はかなりintractableである。しかし、**Kantorovich-Rubinstein duality [22]**は次を示している。

W(\mathbb{P}_r , \mathbb{P}_{\theta}) = 
 \underset{\parallel f \parallel_{L \leq 1}}{sup} \mathbb{E}_{x\sim\mathbb{P}_r}[f(x)]-\mathbb{E}_{x\sim\mathbb{P}_\theta}[f(x)] \tag{2}

1リプシッツな関数fに関して、２つの分布からそれぞれｘを入力して、そのfの期待値の差の上限が$W(\mathbb{P}_r , \mathbb{P}_{\theta})$となる。
上限というのは、集合内にその上限を超える値はないが、上限より少しでも下げると集合内に上限を超えるものが現れるような値。

[メモ]
リプシッツ連続性：

函数のより強い形の一様連続性である。直観的には、リプシッツ連続函数は変化の速さが制限される。即ち、適当な有限値の実数が存在して、その函数のグラフ上の任意の二点を結ぶ直線の傾きの絶対値はその実数を超えない。この上界をその函数の「リプシッツ定数」（あるいは一様連続度（英語版））と呼ぶ。例えば一階微分が有界な任意の函数はリプシッツである

メモここまで。

ここでsupremumはすべての1-Lipschitz関数$f: \chi \rightarrow \mathbb{R}$上で取る。$\parallel f \parallel_{L \leq 1}$を$\parallel f \parallel_{L \leq K}$(定数Kの関するK-Lipschitzを考える)に置き換えれば、$K\cdot W(\mathbb{P}_r , \mathbb{P}_{\theta})$となる。ゆえに、Kに関する全てのK-Lipschitz関数のparameterized family {${ f_w
}$}$_{w \in W}$があれば、次の問題を解くことが考えられる。

\underset{w\in W}{max} \mathbb{E}_{x\sim\mathbb{P}_r}[f_w(x)] -\mathbb{E}_{z\sim p(z)}[f_w(g_{\theta}(z))] \tag{3}

wによって値が決まるkリプシッツな関数fの、それぞれの分布での値の期待値の差を、wを変えて最大化する

そして式(2)の上限がなんらかの$w\in W$について達成されるなら（かなり強い仮定である。推定器の一貫性を証明する時に仮定するものにている）、このプロセスは$W(\mathbb{P}_r , \mathbb{P}_{\theta})$を定数係数まで(の誤差で)計算できる。
さらに、$\mathbb{E}_{z\sim p(z)}[\nabla_\theta f_w(g_{\theta}(z))]$を推定しながら式(2)をバックプロップして（また定数誤差で）$W(\mathbb{P}_r , \mathbb{P}_{\theta})$を微分することを考えられる。
これはすべて直感であるが、今これが最適性推定(optimality assumption)の下で原理化されることを証明する。

定理3.

$\mathbb{P}_r$を任意の分布とする。$\mathbb{P}_\theta$を、$g_\theta(Z)$の分布とする。ここでZは密度pを持つランダム変数、$g_\theta$は仮定1を満たす関数。このとき、次の問題に対して解$f: \chi \rightarrow \mathbb{R}$が存在する

\underset{\parallel f \parallel_{L \leq 1} }{max} E_{x\sim\mathbb{P}_{r}}[f(x)]-E_{x\sim\mathbb{P}_{\theta}}[f(x)]

式(2)のsupがmaxになったもの。
また、次を得る

\nabla_\theta W(\mathbb{P}_r , \mathbb{P}_{\theta}) = - \mathbb{E}_{z\sim p(z)}[\nabla_\theta f( g_{\theta}(z))]

勾配は増加方向だから負号。$\mathbb{P}_r$のほうは~~考えなくて良いのか？~~アルゴリズム１にはそちらもある。これはGの更新用。
どちらもwell-definedであるときに限る。

証明

付録C参照

今、式(2)の最大化問題を解く関数fを見つける問題を考える。これを大まかに近似するために、典型的なGANでやるように、コンパクト空間Wにある重みwでparameterizeされたニューラルネットを$\mathbb{E}_{z\sim p(z)}[\nabla_{\theta} f( g_{\theta}(z))]$を通してバックプロップで訓練することができる。Wがコンパクトであるということはすべての関数$f_w$が、個別の重みwではなくWにのみ依存するようなあるKについてK-Lipschitzであることを意味する。Wがコンパクトであるというのはwの値が有界になるということ。wが有界ならある２つの入力に対する関数fのそれぞれの出力の間の距離は、もともとの入力間の距離の定数K倍に抑えられ、つまりKリプシッツとなる。したがって、式（２）の近似は無関係なスケーリング要素と”critic”$f_w$の容量(capacity)まで近似できる。
criticはDiscriminatorの連続版。
コンパクト：
「位相空間の部分集合について、その任意の開被覆が有限部分被覆を持つことをコンパクトと言う。」, 「コンパクトな集合」≒「有界な閉集合」

パラメータwがコンパクト空間にあるためにできることで、シンプルなのは各勾配更新のあとに重みを固定のボックス(例えば$W=[-0.01, 0.01]^l$)でクランプすることである。単純に重みの各次元の大きさをクリッピングすること。"ボックス"とあるのは多次元のため。
Wasserstein Generative Adversarial Network (WGAN)の手順はアルゴリズム１の通り。

アルゴリズム１:WGAN
すべての実験はデフォルトパラメータ$\alpha=0.00005, c~0.01, m=64, n_{critic}=5$で行った。

• Require:
  • 学習率$\alpha$,
  • クリッピングパラメータc,
  • バッチサイズm,
  • Generatorイテレーション１回につきcriticのイテレーション回数$n_{critic}$
• Require:
  • 最初のcriticのパラメータ$w_0$
  • 最初のgeneratorのパラメータ$\theta_0$

• while $\theta$が収束していない do
  • for $t=0,...,n_{critic}$ do
    • 真のデータのバッチから$\{x^{(i)}\}_{i=1}^m \sim
      \mathbb{P}_r $をサンプルする
    • 事前分布のバッチから$\{z^{(i)}\}_{i=1}^m \sim
      p(z)$をサンプルする
    • $g_w \leftarrow \nabla_{w}[\frac{1}{m}\Sigma_{i=1}^{m}f_w(x^{(i)})-\frac{1}{m}\Sigma_{i=1}^{m}f_w(g_\theta(z^{(i)}))]$ 誤差関数の勾配計算
    • $w \leftarrow w + \alpha \cdot RMSProp(w, g_w)$ 重みの更新
    • $w \leftarrow clip(w, -c, c)$ 重みのクリッピング
  • end for
  • 事前分布のバッチから$\{z^{(i)}\}_{i=1}^m \sim
    p(z)$をサンプルする
  • $g_{\theta} \leftarrow -\nabla_{\theta}[\frac{1}{m}\Sigma_{i=1}^{m}f_w(g_\theta(z^{(i)}))]$
  • $\theta - \alpha \cdot RMSProp(\theta, g_{\theta})$
• end while

重みクリッピングは明らかにLipschitz制約を課すには悪い方法。もしクリッピングパラメータが大きければ、重みが上限に達するのに長い時間がかかり、criticを最適点まで訓練するのが難しい。すべてが上限まで行く必要があるのか？
もしクリッピングが小さければ、レイヤ数が大きい時や(RNNなどで)batch normalizationを使わない時に簡単に勾配消失する。ほとんど変わらない(重みを球に投影するような)シンプルな変種で実験したが、weight clipping はシンプルであるし、すでに良い性能なのでそこにとどまった。結局クリッピングにした。
しかしこの問題はさらなる調査が必要だし、興味がある研究者は積極的にこれを改良してほしい。別のauthorによりwgan-GPとして改良されている。

EM距離が連続でほとんどいたるところで微分可能であることはcriticを最適まで訓練でき、またすべきであることを示す。論点はシンプルで、criticを訓練するほど、より信頼できるWassersteinの勾配が得られる。これはWassersteinがほとんどいたるところで微分可能であるという事実のためで、実際に有用である。
JSについては、Dがよくなるほど勾配はより信頼できるが、JSが局所的に飽和されたとき勾配が０になり、勾配消失する。これは図1や[1]の定理2.4の通り。EMでは局所的に飽和はないんだろうか
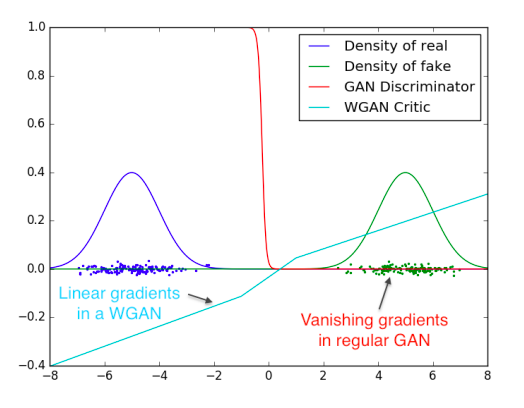
図2にこの概念の証明を示すが、GANのDとWGANのcriticを最適点まで訓練している。Dはfakeとrealを見分けることをかなり早く学習するが、予想通り信頼できる勾配情報を提供しない。

図2:2つのガウシアンを区別することを学習した最適なDとcritic
minimaxGANのDは飽和し、勾配消失する。WGANのcriticは空間のすべての箇所でクリーンな勾配を提供する。

重みを制限したことは関数の可能な成長が空間の中の異なる部分でせいぜい線形になるように制限しており、最適なcriticがこの振る舞いをすることを強制している。?

もっと重要なことは、criticを最適点まで訓練できることはモードコラプスが起こりえないということ。これはモードコラプスが、固定のDに対して最適なGとはDが最も高い値を出す点のデルタ(deltas)の和であるという事実から生じることによる。[4]で観測され、[11]で議論されている。??Dが最も高い点とは本物データの場合を指す。本物っぽい点の平均みたいなものがGだという意味?

次章では実利について書き、従来のGANとの詳細な比較を行う。

4. 経験的な結果

WGANで画像生成実験を行い、通常のGANより実用的な利点が多いことを主に２つ示す。

• Gの収束と生成品質が相関する意味のある誤差関数
• 最適化工程の安定性向上

###4.1 実験手順

• 画像生成。
• 学習するターゲット分布はLSUN-Bedrooms dataset [24]。
• ベースラインはDCGAN [18]。
• 生成画像は3channel, 64x64pixel。
• アルゴリズム１のパラメータ設定を使用

###4.2 意味のある誤差関数
WGANは各Gの更新(10行目)の前によくcritic fを訓練する(2-8行目)。このときの誤差関数はEM距離の推定である。（誤差はfのLipschitz定数を制約したやり方に関する定数項まで）。

最初の実験はこの推定が生成サンプルの品質とどの程度相関するかを示す。DCGANと合わせて、G、またはDとG両方を4-layer ReLU-MLP(512隠れユニット)に置き換えた実験も行った。

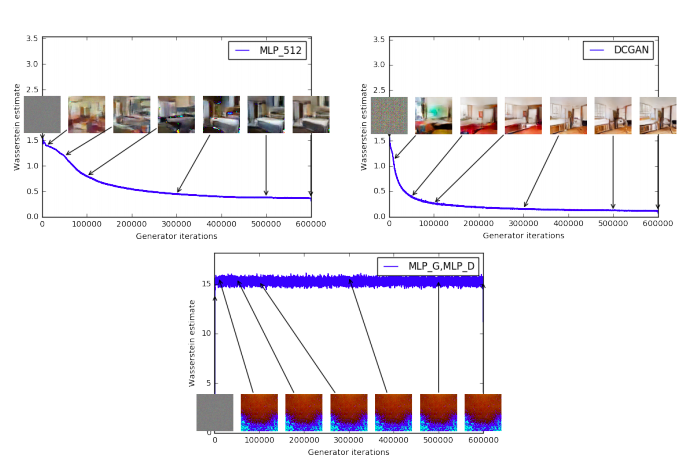
図3はWGANによるEM距離の式(3)の推定の時間発展を他のアーキテクチャに対してプロットしている。プロットから明らかに、この曲線が生成サンプルのvisual qualityと相関している。

図3:訓練の色々な段階での訓練カーブとサンプル
低いエラーと良いサンプルには明らかな相関が見られる。

• 左上：GはMLP(4隠れ層、512ユニット)。訓練に伴い誤差は減少し、サンプル品質も上がる。
• 右上：Gは普通のDCGAN。誤差は早く減少しサンプル品質も上がる。上段はどちらもcriticはシグモイドのないDCGANであるので、誤差は比較できる。
• 下段：DもGもMLPで、実質的に学習率が高い。(故に訓練失敗している)。誤差は一定でサンプルも同様。訓練カーブは可視化のためにメディアンフィルタを適用した。

知りうる限り、GANの研究で、その誤差が収束の性質を見せたのはこれが最初である。生成サンプルを眺めてモード崩壊がないか確認する必要がなく、どのモデルが優れているか示す情報が増えるので、GANの研究でこの性質は極めて有用。

だが、これが生成モデルの定量的評価における新手法だとは言わない。criticの構造に依存する定数のスケーリング要素のために、異なるcriticでモデル比較することは難しい。さらに、現実にはcriticは無限の容量を持たないのでこの推定がEM距離とどのくらい近いのか知ることは難しい。そう言っても、実験で繰り返しこの手法を使ってのバリデーションに成功しており、著者らは以前にはそのような手法がなかったGAN訓練の大きな改善と見ている。

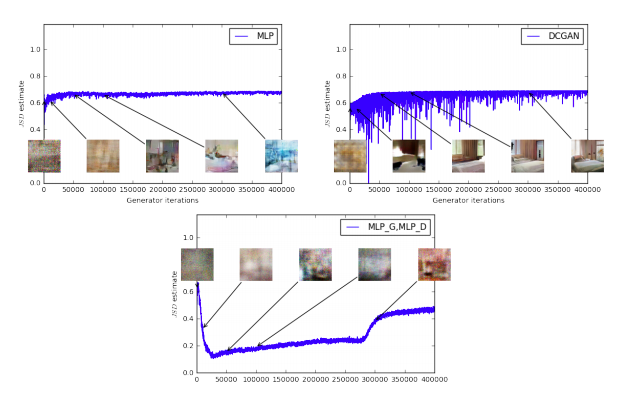
図4は訓練中のJS距離の推定の時間発展をプロットしている。正確には、GAN訓練中に、Dが次を最大化するよう訓練される

L(D, g_\theta) = \mathbb{E}_{x\sim \mathbb{P}_r}[logD(x)] + \mathbb{E}_{x\sim\mathbb{P}_{\theta}}[log(1-D(x))]

これは$2JS(\mathbb{P}_r,\mathbb{P}_{\theta})-2log2$の下限である。図ではJS距離の下限である$\frac{1}{2}L(D,g_{\theta})+log2$をプロットした。
この量はあきらかにサンプル品質と相関が低い。JSの推定はいつも定数か、下がるのではなく上がることも注意してほしい。実際その値は$log2 \approx 0.69$に非常に近い所でとどまるが、これはJS距離が取りうる最大値である。言い換えれば、JS距離が飽和する、Dの誤差が０になる、そして生成サンプルは意味がある場合もある（DCGANのG、右上）が、そうでなければ１種類の無意味な画像になる[4]。この現象は理論的に[1]で説明され[11]でハイライトされている。
**− log D trick [4]**を使った場合、DとGの誤差は異なる。付録Eの図８は同じプロットを示すが、Dの誤差ではなくGの誤差を使用している。結論は変わらない。
サンプル品質と誤差の低さに相関がある

図4：通常のGAN手順で訓練されたMLPのG(左上)、DCGANのG(右上)のJS推定。どちらもDCGANのDを持つ。
両方とも誤差が上昇している。DCGANのサンプルは良くなっているが、JS推定は増加するか一定であり、サンプル品質と誤差には大きな相関はない。
下段：GとD共にMLP。曲線はサンプル品質と関係なく上下している。すべての訓練カーブは図３と同じメディアンフィルタを適用している。

最後に、ネガティブな結果として、WGANの訓練がAdam[8]　($\beta_1 >1$)のようなモメンタムベースのオプティマイザをcriticに使ったり、学習率が高すぎると不安定になることを報告する。criticの誤差が非定常なので、モメンタムベースでは性能が悪化する。モメンタムが原因だと特定したのは、誤差が跳ね上がり、サンプルが悪くなり、Adamステップと勾配とのコサインが負になったから。このコサインが符になるのは不安定のケースだけであった。したがってRMSProp[21]に変更したが、これはよく動作する。いかなる非定常問題でも[13]

4.3 安定性向上

WGANにはcriticを最適まで訓練できる利点があった。criticが完了まで訓練したとき、Gに誤差を提供する。（完了すれば、Gは他のNN同様に普通に訓練できる）。つまりGとDの容量を適切にバランスする必要がない。criticが良いほどGの訓練に良い勾配を利用できる。
WGANはGの構成を変えた時GANよりロバストである。３つの実験で示した：

1. DCGANのG
2. batch normalicationなしで、フィルタ数一定のDCGANのG
3. 4層,512ユニットのReLU-MLP

最後の２つはGANではかなり結果が悪いことが知られている。DCGANの構造はWGANのcriticとGANのDでそのまま使用した。
図５、６、７はこれら３つの構造をそれぞれWGAN/GANのアルゴリズムで生成したサンプル。全サンプルは付録F。サンプルの選択は恣意的ではない。
いずれの場合も、WGANアルゴリズムでモードコラプスは観察されなかった。

図5,6,7

5. 関連研究

**Integral Probability Metrics (IPMs) [15]**に関する研究は多い。$F$を$\chi$から$\mathbb{R}$への関数の集合とし、関数のクラス$F$に関連付けられた整数確率メトリック(integral probability metric)として次が定義できる。

d_F(\mathbb{P}_r,\mathbb{P}_{\theta})= \underset{f\in F}{sup} \mathbb{E}_{x\sim \mathbb{P}_r}[(f(x)]-\mathbb{E}_{x\sim \mathbb{P}_\theta}[(f(x)] \tag{4}

全ての$f \in F$について$-f \in F$を得られる(これから考えるすべての例のように)ことは容易に確認でき、$d_F$は非負であり、三角不等式を満たし、対称である。ゆえに、$d_F$は$Prob(\chi)$の擬距離(pseudometric)である。
IPMは似たような式だが、異なるクラスの関数が全然違うメトリックになることを後で見る。

• Kantorovich-Rubinstein duality [22]により、$F$が1リプシッツな関数の集合であれば、$W(\mathbb{P}_r, \mathbb{P}_{\theta}) =d_F(\mathbb{P}_r,\mathbb{P}_{\theta})$である。さらに、$F$がKリプシッツな関数の集合なら、$K\cdot W(\mathbb{P}_r, \mathbb{P}_{\theta})=d_F(\mathbb{P}_r,\mathbb{P}_{\theta})$である。式(2)の右辺が式(4)の右辺のかたちをしているため。このような形の式をIPMというらしい。

• $F$が-1と1の間で制限されたすべての可測な関数の集合(あるいはその区間のすべての連続関数)であるとき、total variation 距離$d_F(\mathbb{P}_r,\mathbb{P}_{\theta})=\delta(\mathbb{P}_r, \mathbb{P}_{\theta}) $を得る[15]。このことは1リプシッツから1-Boundedな関数になると空間のトポロジを劇的に変え、$d_F(\mathbb{P}_r,\mathbb{P}_{\theta})$の誤差関数としての正則性(regularity)を変える(定理１，２のように)ことを示している。1boundedより１リプシッツのほうが今の問題には都合が良い。というか1リプシッツでなければ学習できない

• **Energy-based GANs (EBGANs) [25]**はtotal variation距離に対する生成的アプローチだと考えられる。この関係は付録Dで証明する。この関係のコアは、Dが式(4)を最大化するfの役割をするということ。ただし何らかの定数mについて0からmまでという制限がある。Dの役割は同じだが、EBGANの場合その出力は0~mに収まるということだろうか。これは-1〜1に制限した場合と同様の振る舞いをする(最適化に関係ない定数倍まで)。ゆえに、Dが最適になるとGのコストはTV距離$\delta(\mathbb{P}_r, \mathbb{P}_{\theta}) $を近似する。TV距離はJSと同様のregularityを示すので、EBGANはDを最適まで訓練できず、完全でない勾配しか使えないという点で古典的なGANと同様の問題に陥る。

• Maximum Mean Discrepancy (MMD) [5]はカーネル$k: \chi \times \chi \rightarrow \mathbb{R}$を持つ再生核ヒルベルト空間(Reproducing Kernel
  Hilbert Space (RKHS))$H$ について$F= \{ f \in H: \parallel f \parallel_{\infty} \leq 1 \}$であるとき、IPMの特別なケースである。[5]で証明されているとおり、MMDはカーネルがuniversalなとき擬距離であるだけでなく距離(proper metric)である。特別なケース$H=L^2(\chi, m)$(mは$\chi$上の正規化されたルベーグ測度(Lebsgue measure))では、$\{ f \in C_b(\chi), \parallel f \parallel_{\infty} \leq 1\}$が$F$に含まれ、$\parallel f \parallel_{\infty} \leq 1$は関数のノルム?$d_F(\mathbb{R}_r,\mathbb{R}_{\theta}) \leq \delta(\mathbb{R}_r,\mathbb{R}_{\theta})$となり、ゆえにMMD距離の誤差関数としてのregularityは最低でもTV距離と同じくらい悪いことがわかる。MMDも種々の条件を満たせばIPMと見なせるが、結局TV誤差くらいの悪さとなる。この問題に対して。
  $L^2$空間全体を近似するのに非常に強力なカーネルが必要になるので、これは($H=L^2(\chi, m)$となるのは)かなり特殊なケースである。しかし、[20]で示されたようにガウシアンカーネルでさえ小さなノイズパターンを検出できる。これはとくに帯域幅が低いカーネルで、距離がJSやTVと同様の飽和するやり方に近いことを示している。これは明らかにすべてのカーネルで起こるわけではないが、どの異なるMMDがWassersteinまたはTV距離と近いのかは面白いトピックである。
  MMDの優れた点はカーネルトリックにより、再製核ヒルベルト空間の球(ball)に関して式(4)を最大化する別々のネットワークを訓練する必要がないこと。しかし、MMD距離評価は計算コストが式(4)の期待値の推定に使うサンプル数について２次のオーダーで増加する欠点がある。これがMMDのスケーラビリティを制限し、実問題に適用できなくする。MMDの線形計算コストの見積もりがあり[5]、多くの場合でMMDを便利にするが、サンプルの複雑さが悪化する。

• **Generative Moment Matching Networks (GMMNs) [10, 2]**はMMDの生成版。式(4)のカーネル化版をバックプロップすることで、$d_{MMD}(\mathbb{P}_r, \mathbb{P}_{\theta})$($F$が上記定義のときのIPM)を直接最適化する。式(4)を近似的最大化するのに別々のネットワークが必要ない。だがこのGMMNは適用可能対象が限られる。理由はサンプル数の二次の誤差関数とカーネルの帯域幅が低いための勾配消失。さらに、実際に使えるカーネルは自然画像のような高次元空間の複雑な距離を捉えるのに向いていない。この性質は[19]が示した、典型的なGaussianMMDテストを信頼できる(1に近づく統計テストとしての力のように?)ようにするためには、次元数に対して線形に増えるサンプル数が必要であるという事実によって裏付けられる。実際、普通の64x64画像のようなものなら、最低でも4096のミニバッチが必要(この数をもっと大きくしうる[19]の境界における定数を考慮せずとも)で、$4096^2$のコストがイテレーションごとにかかる。これはbatchsize=64の通常GANのイテレーションより５桁大きい。しかし、これらの値は実際のGANのサンプルの複雑さと、それより悪くなりがちな理論的なMMDのサンプルの複雑さとを比較しているのでMMDにとってアンフェアである。GMMNの元論文[10]ではミニバッチサイズ1000を使用しており、通常の32,64より多い(２次の計算コストがかかるときでも(?))。サンプル数の線形関数の計算コストであるような推定手法[5]もあるが、サンプル複雑性が悪くなるし、知りうる限りGMMNのような生成のコンテクストで使用されたことはない。

他の研究では、[14]はwasserstein距離を離散空間でRestricted Bolzmann Machineの学習に使用している。多様体の設定が連続空間に制限され、 有限離散空間でweak とstrong topologies（それぞれWassersteinとJSの）が一致するため、一見した動機は異なるように見える。しかし、結局は本研究の動機についてそれ以上に共通なものがある。どちらも背後にある空間の幾何を利用する方法で分布を比較したい。そしてWassersteinはそれができる。
最後に[3]は異なる分布間のWasserstein距離を計算する新アルゴリズムを示している。この方向はとても重要で、おそらく生成モデルを評価する新手法につながる。