Azure Cosmos DB とは
2017/05/10(米国時間)にMirosoftから発表されたあたらしいデータベースサービスです。特徴的なのは、これまでのデータベースサービスはいわゆるデータセンターに閉じた状態での分散レベルしか提供してこなかった所を、データセンターを跨ぐレベル(惑星規模とか言われる)でサポートしている所です。ホストするデータがどこまででも大きくなれますよ(スケーラビリティ)というよりも、複数の地理的に遠く離れたデータセンター拠点に跨ってデプロイできて、一つのデータセットにアクセスできるよという意味です。これに先立ってGoogleから発表されたSpannerも惑星規模で分散できるサービス(マルチリージョン対応はこの記事執筆時点では未対応)ですよね。
米MS、「惑星規模」でスケールする「Azure Cosmos DB」を発表
Azure Cosmos DBは惑星規模の分散環境をサポートする、という以外にも下記の特長を持っています。
- Multi-Data: テーブル、Document、グラフ、Key-Valueといった様々なデータに対応
- それぞれ DocumentDB API, MongoDB API, Table API,Graph API(Gremlin対応)といったAPIでアクセス可能
- ペタバイトレベルまでスケール可能
- 5つの一貫性レベルに対応(Strong, Bounded Staleness, Session, Consistent Prefix, Eventual Consistency)
を持っています。
この記事では、この中でもCosmos DBがサポートする 5つの一貫性レベル という性質、そのなかでも Bounded Staleness という一貫性レベルにフォーカスします。この概念がどういう一貫性を提供するのか、そして、その一貫性レベルを__Probabilistic Quorum__ という手法をつかってどう実現できるのか?についてフォーカスします1。
なぜ5つの内それにフォーカスするかというと、個人的な理由になってしまいますが、2点あります。
-
個人的に、Strong、いわゆるLinearizabileと呼ばれるような「強い一貫性」と、Eventual Consistentと呼ばれる、いつかは整合が取れるけどそれがいつかは保証しませんよ、という「弱い一貫性」の中間の定義は、恥ずかしながらこれを見るまで知らなかったため、この定義を見た時には、非常に新鮮で興味がそそられた
-
最近ずっと、Quorum呼ばれる概念とその応用について大変興味を持っていて2、5つのレベルの中でBounded Stalenessと呼ばれる整合性を実現する手段としてProbabilisic QuroumというQuorumの一種が利用可能であることがわかった
-
この不思議な性質と構成法は、Quroumの応用としてとてもシンプルかつ実用的だと感じた
ためです。
その他のCosmos DBについての情報は下記を参照ください。
- 米MS、「惑星規模」でスケールする「Azure Cosmos DB」を発表
- A technical overview of Azure Cosmos DB
- Azure Cosmos DB Documentation(公式ドキュメント)
ではまず、Azure Cosmos DBでサポートされる5つのConistency Levelから見ていきましょう
Azure Cosmos DB で導入された 5つ のConsistency Level
5つのConsistency Levelは公式DocumentのConsistency Levelのセクションを参照してみます

公式Documentから引用
左に行くほど、整合性が強く、右に行けば右に行くほど整合性が弱いです。「整合性」とは、をここで詳しく説明するよりも、それぞれの整合性レベルを説明しながら感覚をつかむ方がやりやすいと思います。整合性が弱い方から順番にカンタンに説明していきます。
下記の整合性レベルを読み進める時は、「複数のデータレプリカをどう管理するか?」という事を念頭において読み進めると読みやすいです。分散データベースにおいては、可用性、スケーラビリティを高めるために、どうしても一箇所にデータを書くというのでは回りません。そうなるとどうしてもデータの複製(replica)を幾つかの場所で保持せざるをえず、そうなるとそのレプリカを「どうやって管理していくか」という方法がとても大事になります。
- Eventual
- 読み込めるデータが 最新である保証はない
- 読み込むプロセスによって(同一プロセスであっても)は 先祖返りするかもしれない
- でも、すべてのreplicaが いつか同じ状態に収束する
- これは5つの内一番整合性が弱いかわりに読込書込がとても速い
- Consistent Prefix
- 読み込めるデータが最新である保証はない,先祖返りするかもしれない, いつか同じ状態に収束する のは__Eventualと同じ__
- それに加えて__replicaに適用される書込リクエストの順序は同じ__
- 例えば、
A, B, Cという書込リクエストが複数のreplicaに適用されるとすると、クライアントからみると、A,A,B,A,B,Cと書込リクエストが処理されたデータは読み込まれる可能性はあるが、 -
A,Cとか、B,A,Cという風な順で書込がなされたデータが見える可能性はない
- 例えば、
- Session
- Consistent Prefixは、先祖返りが起きたり, 読込リクエストごとに見えるデータの世代が違う、ことが起きるけれど、
- Sessionでは、いわゆる__Monotonic Read__, Monotonic Write, __Read Your own Write(RYW)__を保証する
- Monotonic Read: あるプロセスから見て読み込めるデータは先祖返りしない
- Monotonic Write: あるプロセスからなされるデータXへの書込順序は保存される
- Read Your own Write(RYW): あるプロセスが書込処理を行ったら、そのプロセスはすぐその書込処理完了後のデータが読める
- Bounded Stalenss
- 読み込めるデータは古いことはあるが、__t単位時間以降はK世代以内のデータが読める__ことを保証する
- ユーザはこの
K,tをチューニングできる。 - この整合性レベルは、強い整合性を求めたいけどデータのavailabilityが99.99%でよくて、かつ低レイテンシが欲しい場合に有効
- Strong
- いわゆるLinearizabileを保証する、あるプロセスが書き込めたら、どのプロセスが読んでも常に最新の値が読める。
- majority quorumで実装できる
かなり乱暴ですが、まとめると下記の様になるかと思います。
- Eventual: 読み込めるデータはどれだけ古いかわからないけどいつか最新になります(読み込み時先祖返りOK, 書込リクエストの適用順序バラバラもOK)
- Consistent Prefix: いつか最新になればOK(先祖返りも許す)だけど、replicaへの書込リクエストの適用順序は統一
- Session: 自分から見ると先祖返りしない、自分の書込は順序が保たれる、自分の書込は自分からは即読込可能。全体でみるとはConsistent Prfix。
- Bounded Staleness: どのプロセスから見ても、書込後t時間立てば、読めるデータの古さの上限(K世代)が保証される。K, tはチューニング可能。
- Strong: 誰かが書き込んだら、どのプロセス絡みても常に最新の値が見える(K=1, t=0のBounded Stalenessと言える)
概念自体は新しい訳ではない
この発表を見た時はすごく新鮮で面白いな、と思ったのですが、少し調べると、__Bounded Staleness以外は__定義自体そんなに新しいという訳ではありませんでした。
Wikipedia:Consistency Modelを見ると、これらの整合性レベルは2007年にはAndrew Tanenbaum博士によって提唱されているし、
2008年にはAmazon.com CTOであるWerner Vogels氏の記事Eventual Consistent - Revisited.で触れられていました。
とても面白いBounded StalenessというConsistency Level
さて、やっと本題です。Bounded Staleness という Consistency Levelは
どのプロセスから見ても、t時間立てば、読み込める値がK世代以内のデータであることが保証される
と言うものです。
いわゆる強い整合性(このモデルだとt=0, k=1に該当)をもったreplicaの更新はQuorum Systemを使った複製の管理方法で紹介したように
- readとwriteで共通のquorum systemを定義する
- 書込時,読込時にはその中からquorumを一個選んで、quorumに所属するすべてのノードに書込/読込処理を行う(どれか一個でも失敗したらエラーとする)
とすればOKなのですが、
"K世代前"とか、"t時間たったら"を__保証__できるというのがとても興味深いと思いませんか?
僕のこれまでの認識では、quorumは重なっていてこそのquorumでした。writeとreadのquorumが重なっていない場合、古いデータが読めてしまいますが、どうにかしていつか追い付かせたい、と考えると、という意味では、quorumの選び方がランダムでは行けません。いつかread側のquorumが最新のデータ(いくらか古くてもK世代前)のwrite quorumとぶつかるように選んでやらなくては行けません。
例えば、$N$個のreplicaを$N/k$のグループに分割して、書込時は$N/k$個のreplicaをラウンドロビンで選択して更新、読み込む時はどれか1個から読み込む、とかすれば、たしかにreplica内の世代は$k$世代前までしか存在しないので、$k$-世代前は保証できそうです。ただ、$t$時間以降といった制約はちょっとすぐには思いつきません。
が、重なりが一部無いquorum systemであっても、こんな風にやり方と工夫すれば、もっといい具合に全read quorumに少なくとも1つK世代以内のデータが存在するようにwrite quorumを設計できるかもしれませんよね。
鍵となる論文
その答えはAzure Cosomos DBの公式Documentから参照されていました。
Peter Bailis, Shivaram Venkataraman, Michael J. Franklin, Joseph M. Hellerstein, Ion Stoica.
"Probabilistic Bounded Staleness (PBS) for Practical Partial Quorums."
http://vldb.org/pvldb/vol5/p776_peterbailis_vldb2012.pdf
です。
此処から先はこの論文を抜粋して、できるだけわかりやすく、
Probabilistic Bounded StalenessをProbabilisitic Quorum Systemをつかって実現する方法
を解説していきたいと思います。
Partial/Probabilistic Quorumとは
先に述べたように、通常のquorum system(ここではprobabilistic/partialと対比してstrict quorum systemと呼ぶ)はこの定義にあるように
定義 ノードの集合を$V = \{ v_1, v_2, ..., v_n \}$とする。Strict Quorum Systemとは$V$の部分集合の集合 $\mathcal{S} \subset 2^V$ で次の条件を満たすものを言う。 $\mathcal{S}$の要素をQuorumと呼ぶ
- どの2つのQuorum $Q_1, Q_2$も共通部分を持つ($Q_1 \cap Q_2 \neq \emptyset$)
なわけですが、このintersection criteriaを緩和してみようと思うと、自然に次のPartial Qurorumという概念が定義できます
- Parial Quroumであるための条件: 少なくとも2つのQuorum $Q_1, Q_2$が共通部分を持たない($Q_1 \cap Q_2 = \emptyset$)
実用上、全く重ならなくても困るし、重なる可能性も議論できないので困るため、Partial Quorum System上に、どのQuorumがどのくらい選ばれるか?というaccess strategyを導入して、そのaccess strategy上でQuorum同士が重なる確率を保証するようなProbabilistic Quorumも定義されます。
- $\epsilon$-Probabilistic Qurorumであるための条件: $Pr_\omega [Q \cap Q' \neq \emptyset]\geq 1-\epsilon $
- $\omega$はquorum systme上のaccess strategy
Probabilistically Bounded Staleness (PBS)
この論文では3つのProbabilistic Bounded Stalenessとして、PBS k-staleness, PBS t-visibility, PBS -stalenessを定義しています。
- PBS $k$-staleness: 確率的に$k$世代以内が読める
- PBS $t$-vibibility: 確率的に$t$時間以降は最新世代が読める
- PBS $<k,t>$-staleness: 確率的に$t$時間以降は$k$世代以内が読める
です。
Probabilistic Bounded Stalenessは、日本語に訳すと、「確率的に」「保証できる」「データの古さ」とでもなるでしょうか。
このPBSを定義する上では、前提として上のように一つのqurorum systemをread,writeで共有するモデルではなく、read quorum, write quorumを別々に用意するモデルを前提にしています。また、visibilityを定義する上では書込処理後にanti-entropy処理を行うexpanding quorumが前提となっています。
順に定義と構成法を見ていきましょう。
PBS k-Staleness
k-stalenessの定義は次のとおりです。
定義 Quorum System が PBS k-staleness consistencyを満たす、とは、read quorumの少なくとも一つのデータが$1-p_{sk}$の確率で$k$世代以内のデータを含む事を言う
構成法
いわゆるDynamoスタイルのRead/Write Qurorumシステムを考えます。$\mathcal{S} = 2^V$上のaccess strategyとして
- 読込時: $\mathcal{R} = \{ s \in \mathcal{S} ,|, |s| = R \}$からrandomに選択 (N replicaからrandomに$R$個選ぶ)
- 書込時: $\mathcal{W} = \{ s \in \mathcal{S}| ,|, |s| = W \}$からrandomに選択 (N replicaからrandomに$W$個選ぶ)
を考えます。 DynamoやCassandraはでは$R + W > N$となるようにすることで、WriteとReadのquorumが必ず重なるようにして強い整合性を提供しています。が、ここではその制限をせずに、単純に何の制約もない$R, W$の場合を考えます。
このaccess strategyの元で、読込時に最新バージョンが含まれない確率$p_s$(stalenessのs)はどう計算されるでしょう? 書込時に使われたQuorumの特定の$W$個のノードがRead Quorumとして選ばれない確率を計算すれば良いだけなので、
$p_s = \frac{直前にWriteされたWノードを覗いた母集団から上のRead Qurorum数}{|\mathcal{R}|} = \frac{N-W \choose R}{N \choose R}$
この値がどうなるかを幾つかの$N, W, R$で調べてみると面白いことがわかります
- $N = 3, R = W = 1 \Rightarrow p_s = 2/3 $
- $N = 100, R = W = 30 \Rightarrow p_s = 1.88 \times 10^-6$
一般的に各keyについて100個もreplicaは作りませんから、よく用いられる$N=3, R = W = 1$だとすると、$2/3$の確率で最新が読めないということになります。裏を返せば$1/3$の確率で最新が読める事になります。
もうお気づきでしょうか?最新($1$世代前)が読めない確率$2/3$なわけですが、$k$世代前までOKとすると、$k$世代前までが全く読めないという確率は$p_s^k$で計算できるので、結果的に$k$世代以内が取れる確率はどんどん上がるわけです。
- $N=3, R=W=1$の場合、$k=10\Rightarrow 1-p_{sk} > 0.98$
- $N=3, W=2, R=1$(逆でも同じ)の場合、$k\geq5 \Rightarrow 1-p_{sk} > 0.995$
- $N=5, W=2, R=2$の場合$p_{s1}=3/10$, $k\geq5 \Rightarrow 1-p_{sk}>0.997$
となります。つまり
- N=5(replica数=5)
- R=2(Read時replicaからランダムに2個読んで新しい方を返す)
- W=2(Write時もreplicaを2個ランダムに選んで更新)すると、
- 99.7%の確率で5-stalenessを満たす
ということが分かりました。こんな単純なロジックでも$5$世代以内という条件なら99.7%以上の確率というのが興味深いですね。
PBS t-visibility
Read/Write Qurorumを使ったreplica管理をする場合、write要求処理時、W個のreplicaに書き込むわけですが(W個に書き込んだ後処理完了をclientに返す)、その後非同期でN個のreplicaにwrite要求を伝播させるanti-entropyという呼ばれる処理が行われる事が多いです。write qurorumが拡大していく様子からexpanding quorumとも言われます。
t-visibilityでは、expanding quorumモデル上で、どのくらい時間が立てば、最新世代が読み込めるようになるかという、"inconsistency window"とも呼ばれる指標を定義します。
定義 quorum system が PBS t-visibility consistencyを満たす、とは少なくとも$t$単位時間後には、すべてのread quorumの少なくとも一つのデータが$1-p_{sk}$の確率で_最新_世代のデータを含む事を言う
構成法
expanding quorumを使った、replica管理アルゴリズムを再度確認しましょう
- Write時:
- N個のreplicaからランダムにW個選び書き込む(Write Qurorumに書き込む)
- clientはW個書込完了時点で成功を受け取る
- その後残りのreplicaに順に値を伝播させていく(anti-entropy処理)
- Read時:
- N個のreplicaからランダムにR個から読み込んで一番新しい世代を返す
です。
この単純なアルゴリズムがどのくらいのinconsistency windowを持つか評価するために、anti-entropyプロセスを特徴づける、最新世代のreplica数に関する累積確率関数をを使って評価します。
- $t$単位時間後に$w$個のreplicaが最新である確率を $P_\omega(w,t)$ とする
- expanding quorumの書込処理の定義から $\forall c\in[0,W],,P_{\omega}(c,0)=1$ことに注意
こうすると、$p_{st}$(t単位時間たった後、最新の世代を含まないread replicaにアクセスされる確率)は次のように計算できます
\begin{align}
p_{st} &= (t=0で書き込まれたWrite Quromにアクセスできない確率) \\&\quad + (t単位時間後に最新版を持っているreplicaにアクセスできない確率) \\
&= \frac{N-W \choose R}{N \choose R} + \sum_{c\in(W,N]}\frac{N-c \choose N}{N \choose R} (P_\omega(c+1,t)-P_\omega(c,t))
\end{align}
この確率は$t$時間後ピッタリにreadを行う点、W個のwrite直後(delay無く)からanti-entropy処理が始まると過程された場合の確率なので、実際での$p_{sk}$の上界になります(つまり実際には、最新世代にアクセスできない確率はこの値より小さくなる)。
また、この$P_\omega$というのはanti-entropyプロセス自体に依存するので、これ以上の解析は出来ません。実用性のセクションで具体的なanti-entropyプロセスを想定したシミュレーション結果が示されます。
PBS k,t-staleness
$t$-visilityを持つexpanding quorumを使ったシステムに、$k$-stalenessの概念を組み合わせたのが$<k,t>$-stalenessです。つまり、$k$回の書込が完了してから$t$単位時間後にReadリクエストがあった時に、その時点での最新版から$k$世代以内のデータにアクセスできることを確率的に保証します。
定義 quorum system が PBS $<k,t>$-stalness consistencyを満たす、$k$回の書込後$t$単位時間後にreadがrequestされた時、すべてのread quorumの少なくとも一つのデータが$1-p_{skt}$の確率でその時点での最新世代から$k$世代以内のデータを含む事を言う
構成法
t-visibilityと全く同じexpanding quorumを採用出来ます。このモデルのまま、$t$時間後に$k$世代以内が読める確率を計算できます。厳密に計算しようとすると、$k$個のwrite間の時間差を考慮することも出来ますが、ここでは全てのwriteが同時に起きたとして計算すると、$k$-stalenessで計算したように、下記のように単純に計算できます
$$
p_{skt} = p^k_{st} = \left(\frac{N-W \choose R}{N \choose R} + \sum_{c\in(W,N]}\frac{N-c \choose N}{N \choose R} (P_\omega(c+1,t)-P_\omega(c,t))\right)^k
$$
ココでも結局$t$-visibilityの時と同じようにanti-entropyプロセスに依存する$P_\omega$に依存する確率になってしまいます。
Probabilistic Bounded Stalenessの実用性
論文では、実用的によく使われるDynamoスタイルのexpanding quorum system(WARSモデル)をベースに、その管理方法がどのくらいの$$-Stalenessを満たすかがシミュレーションで示されていました。
Dynamoスタイルのquorumシステム: WARSモデル
Dynamoスタイルのquorumシステムは先に示したexpanding quorumベースのreplica管理アルゴリズムとなっています。このアルゴリズムでは明にquorumを選択せずに、全replicaに要求を送り、早い者勝ちでreplicaから返ってきた返答を使ってclientに返答します。
- Write時: N個のreplica全てにwriteリクエストを送る。W個の返答が返ってきた時点でclientに完了返答
- Read時: N個のreplica全てにreadリクエストを送る。R個の返答が返ってきた時点で最新版をclientに返答
これを図示すると下図のようになります
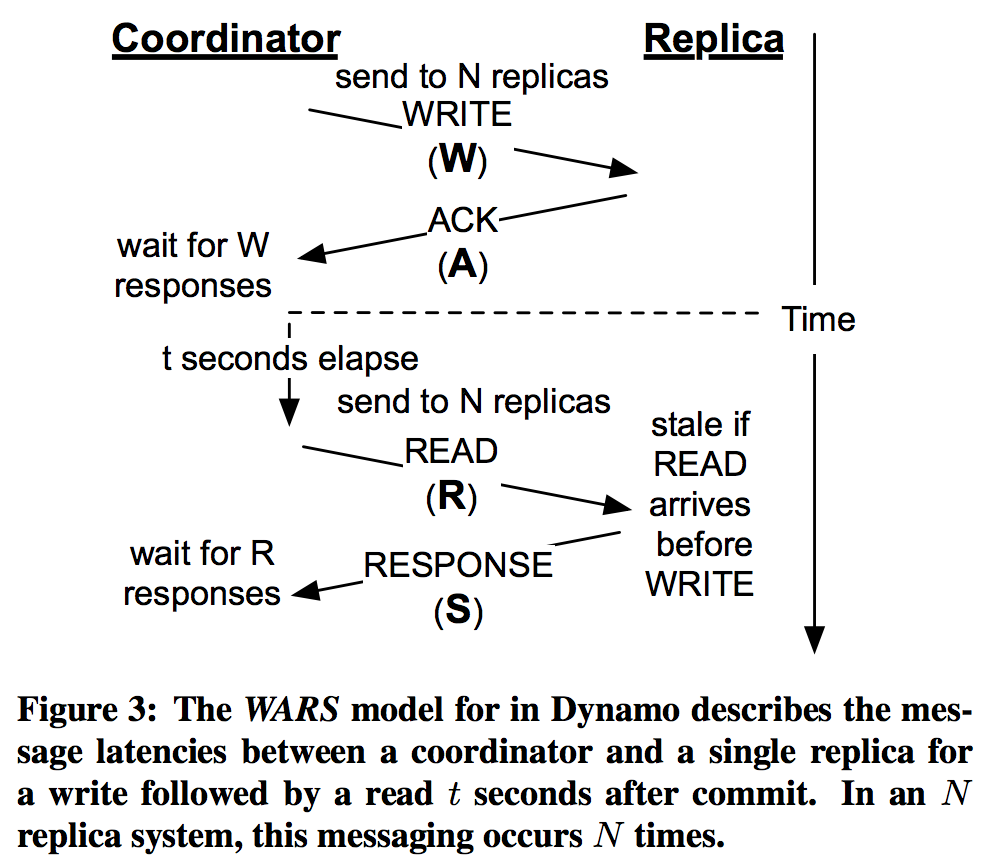
※論文から引用
WARSモデルにおけるt-visibility
$<k,t>$-stalenessの確率は$t$-visibilityのそれから求まり、$t$-visibilityはanti-entropyプロセスに依存するので、論文では各replica $i$毎にこの図で示される各フェーズの確率分布$\mathbf{W_i},\mathbf{A_i},\mathbf{R_i},\mathbf{S_i}$を様々な値に設定して、MonteCalroシミュレーションによって$t$-visibilityの評価を行っていました。
実験では、LinkedIn, Yammerといった大規模な企業のproduction latencyデータを元に上記の確率分布をパレート分布でモデル化してシミュレーションしていました。詳しい条件は論文のFigure 5.を参照して頂きたいのですが、4つのlatency modelを比較しており、それぞれ次の特長を持っています。
- LNKD-SSD: Voldmortベースのproduction latencyモデル。SSDベースでディスクアクセスは高速。network boundなのでW=A=R=Sを想定
- LNKD-DISK: Voldmortベースのproduction latencyモデル。A=R=SはLNKD-SSDと同じで,Writeだけ遅い
- YMMER: Basho Riackベースのproduction latencyモデル、W, A=R=SというモデルではLNKD-DISKと同じ傾向だが、全体的にLNKD-SSDより遅い。Longtailが太いのが特長で、99.99%tileでは10秒くらいという値もでる
- WAN: readとwriteは異なるdatacenterからくるものと想定。replica requestの一つはdatacenterを跨ぎことを想定。datacenter跨ぎのリクエストはLNKD-SSDモデルに75msを上乗せしている
下記の図は$N=3$で$R,W$を各latencyモデル上で変化させて、$t$-visibilityを満たす確率を算出しています。
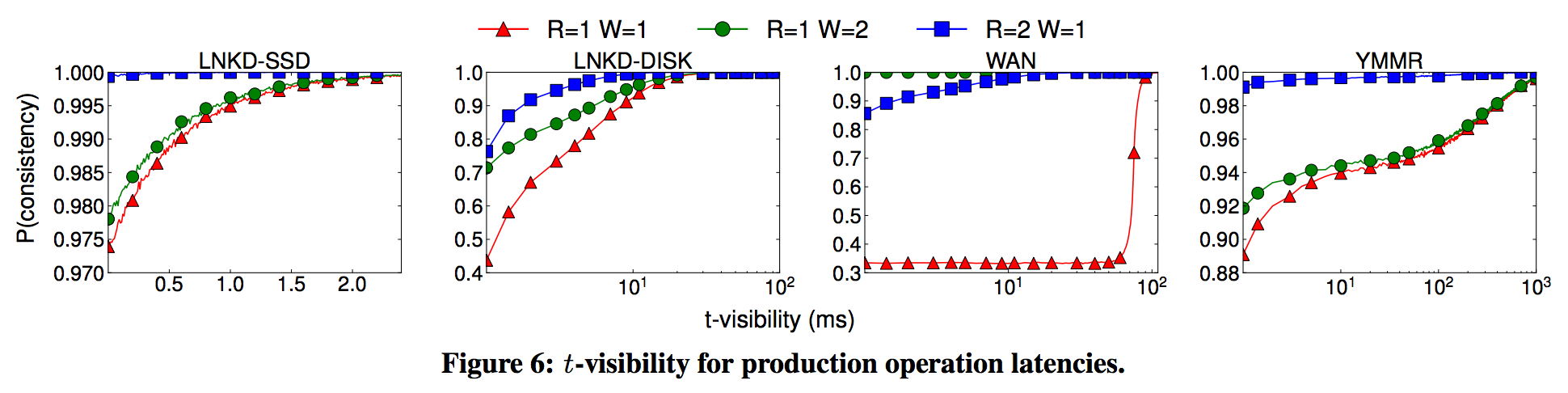
※論文から引用
結果のサマリとして論文では下記が述べられていました。
- $t$-visibilityは総じてwrite latencyに大きく依存する
- LNKD-SSDでは、書込完了直後(t=0)で97.4%, 5ms後には99.999%を達成
- LNKD-DISKでは、writeの遅さが影響し、書込直後では43.99%しか無く、10msたっても92.5%しかなかった
- YMMRでも同じ傾向だが、書込直後で89.3%。99.9%を達成するのに13.64秒かかっていた
- WANモデルは75ms以上立たないとinconsistency windowを抜けないので予想通り遅い。write直後は33%しかない
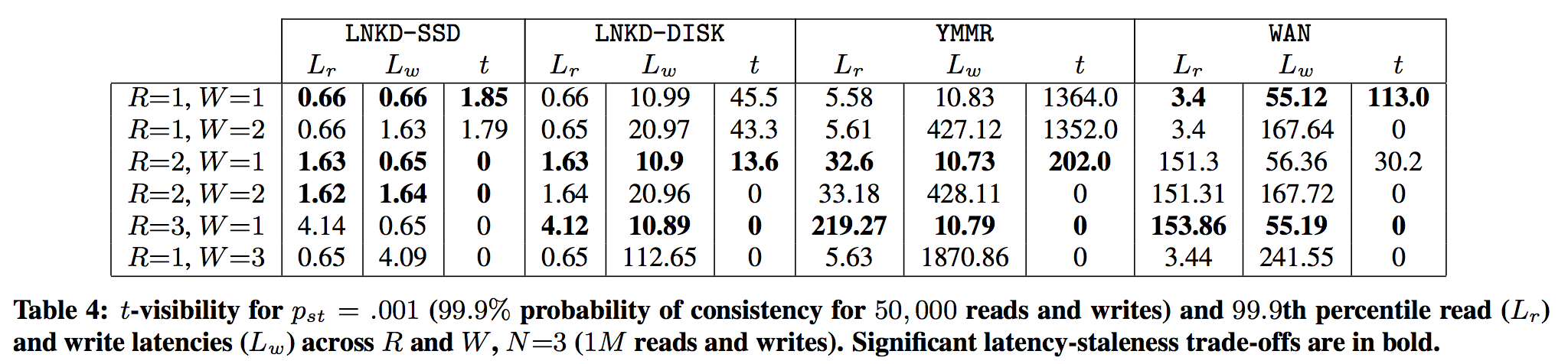
また、$N=3$のもとで99.99%で$t$-visibilityを達成できる$t$の値、read latency, write latencyを各latency modelで算出した表も掲載されていたので載せておく
コレを見ると、
- SSDを使ってディスクアクセスが高速かつ均一な場合、N=3, R=W=1のWARSモデルでは、1.85ms-visilibityが99.99%の確率で達成できる
- DISKでもR=2, W=1としておけば13.6ms-visibilityが99.99%の確率で達成できる
ことがわかります。現在のハードウェア構成を考えると強い整合性(R+W>N)をもって書き込まなくても、t-visibilityがかなり現実的な確率で達成できることがわかります。
もっといろんな場合
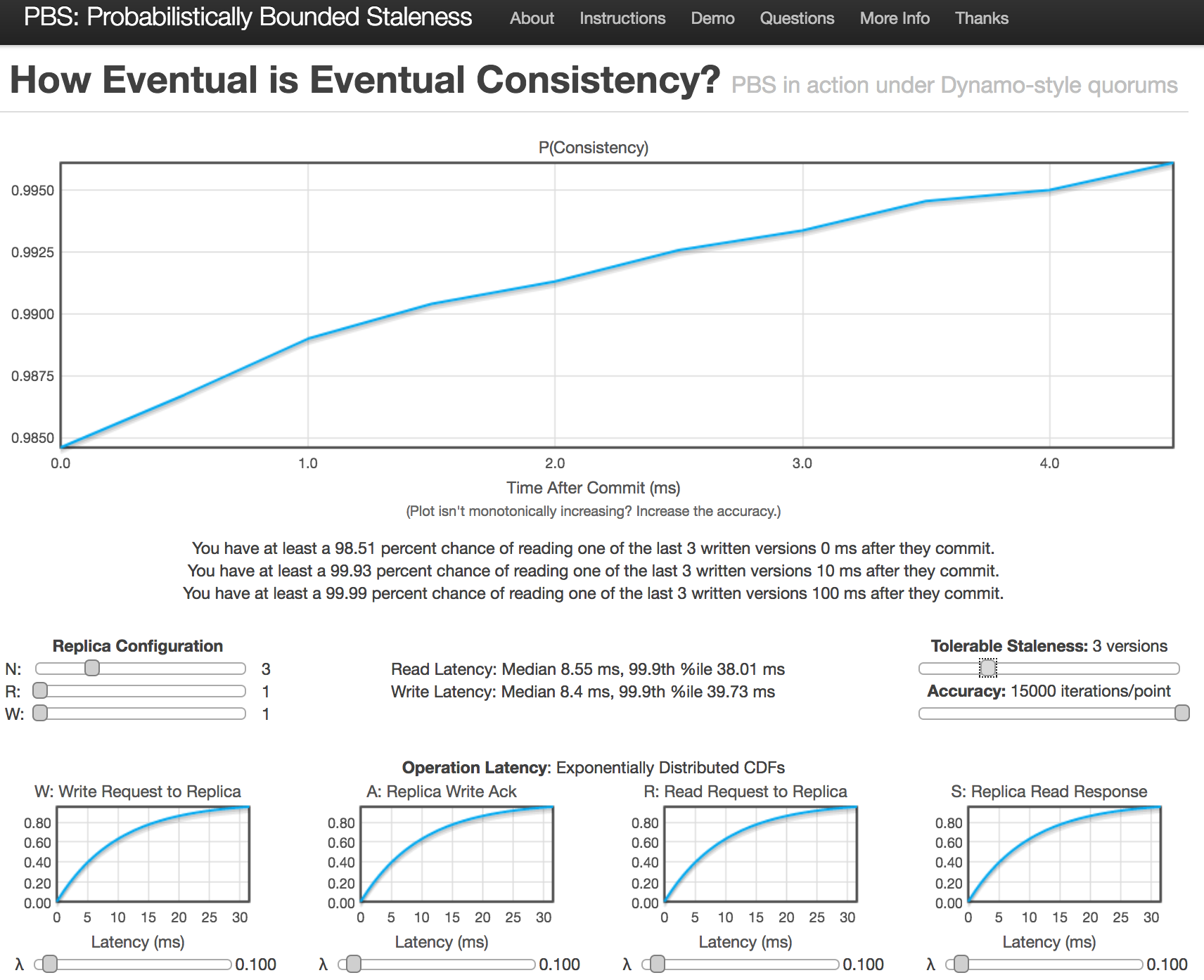
この論文で使われたsimulationはwebから試すことが出来ます。下記をスライダーでセットすると、$<k,t>$-stalenessのグラフがインタラクティブに描画されます。
- qurorumの構成: $N, R, W$
- WARSのlatencyモデル: W,A,R,S
- k-staleness: "Tolerable Staleness"と表現されています
- simulationするためのiteration回数
この図だと、
- $N=3, R=W=1$, $3$-stalenessで設定
- Write直後では75.27%の確率で$3$-staleness
- 10ms後には90.94%の確率で$3$-staleness
- 100ms後には99.99%の確率で$3$-staleness
- が達成できている事がわかります
おわりに
この記事では、Azure Cosmos DBがサポートするデータ整合性レベルの一つであるBounded Stalenessという概念を説明し、
それが、Probabilistic Bounded Stalenessという概念で定式化されること、それが、expanding quorum systemを使うと実現できることを、論文を参照しながら解説しました。
また、Dynamoスタイルのquorum systemであるWARSモデルという単純なアルゴリズムが、非常に実用的なレベルでProbabilistic Bounded Stalenessを満たすことを論文を参照しつつ、インタラクティブシミュレーションデモでも確認しました。
個人的には、単純なread/write quorum + anti-entropyモデルでも、確率的だけれども実用的には強い整合性を期待できる、という点が非常に面白かったし、これがAzure Cosmos DBでプロダクションで採用されているというがとても興味深いです。
A technical overview of Azure Cosmos DBを読んでみると、これまでMirosoftが経験してきたcustomerの傾向に触れているのですが、
About 73% of our customers use session consistency and 20% prefer bounded staleness. We observe that approximately 3% of customers experiment with various consistency levels initially before settling with a specific consistency choice for their application. We also observe that on average, only 2% of our customers override consistency levels on a per request basis.
実際にはあまりBounded Stalenessを選択する人はいないようですね。また、
To report any violations for the consistency SLAs to customers, we employ a linearizability checker, which continuously operates over our service telemetry. For bounded staleness, we monitor and report any violations to k and t bounds. For all four relaxed consistency levels, among other metrics, we also track and report the probabilistic bounded staleness (PBS) metric.
と記されているので、strongを設定した時にちゃんとlineraizabilityが守られているか、bounded stalenessを設定した場合に、$k$や$t$が期待した値を逸脱していないかのアラームもありそうで、とてもおもしろそうです。
実際に自分がAzure Cosmos DBを使う状況になることがあるかどうかはわからないのですが、次は"Session", "Consistent Prefix"といった整合性レベルがどう実装されているのかを調査したいなと思っています。
勉強しながら書いたのでどこか間違っているやもしれません。ツッコミ、フィードバック歓迎します
-
Azure Cosmos DBがここで紹介する手法をそのまま使っているかどうかは定かではない点にご注意ください。だたし、サービスの公式DocumentにおけるConsistency Levelでは、本記事で取り上げる論文が参照されていたり、"For bounded staleness, we monitor and report any violations to k and t bounds. For all five relaxed consistency levels, we also report the probabilistic bounded staleness metric directly to you."という言及がなされているので、本手法もしくは近い手法が使われていると推察されます。 ↩
-
Quorumの基本的理解を助けるために下記のような記事を書きました。最近よく聞くQuorumは過半数(多数決)よりも一般的でパワフルな概念だった ↩