はじめに
生産現場などにおける効率的なオペレーションを目的とした数理最適化問題、特にスケジューリング問題について業務上調べる機会があったので、それについてまとめた記事を書きたいと思います。
対象とする読者層感が分からないまま書いていて、各章ごとで知識レベルのムラがあるかもしれません。誰かの役に立てれば幸いですが、少なくとも自分の知識の整理には役に立っています。
最適化問題とは
- ある制約条件に対して、目的となる値が最もよい(最大・最小)となる状態を求める問題
- 数学的には 、集合$\mathbf{S}$、関数$f: \mathbf{S} \rightarrow \mathbb{R} $に対し、$f(x); (x\in\mathbf{S})$を最小化または最大化する問題
最適化問題の例
- 栄養問題 ... 食品の栄養素(タンパク質・ビタミンなど)と価格から、必要な栄養素を最も安く摂るにはどうしたらいいか
- 巡回セールスマン問題 ... セールスマンが複数の家を訪問する際に、移動距離が最短となるようなルートの求め方
- ビンパッキング問題 ... 大きさの決まった箱と物があり、最も箱の数が少なくなるような物の詰め方
- 輸送問題 ... ある物を供給地(工場など)から需要地(店舗など)に輸送する際に、最もコストが低くなるような流し方
(ジョブショップ)スケジューリング問題とは
- 機械などの希少資源に対し、仕事を最も効率よく割り当てるために、どの仕事をどの時間(順番)で行えばいいかを解く問題。
- 「最も効率よく」の例としては、「最後の仕事が終わる時間が最も早くなる(メイクスパンの最小化)」「納期遅れの合計時間が最も少なくなる」などがある。
問題の種類と例
スケジューリング問題には、解くべき問題に応じて様々な問題設定を作ることができるが、
名前のついたいくつかの典型的な問題が世に知られている。
例として、以下の表のようにジョブ・マシンに対して作業時間が与えられているとする。
| マシン1 | マシン2 | マシン3 | |
|---|---|---|---|
| ジョブA | 3(時間) | 6 | 7 |
| ジョブB | 5 | 8 | 2 |
| ジョブC | 4 | 5 | 6 |
それぞれの機械は同時に複数のジョブを処理することはできないものとする。また、各工程は途中で中断することはできないものとする。
-
オープンフローショップ問題
各仕事の作業順に制限がない場合 -
フローショップ問題
各仕事は、あらかじめ定められた同じ順番(例: マシン1 → 2 → 3)で進めなければならない場合 -
ジョブショップ問題
各仕事は、仕事ごとに定められた順番で進めなければならない場合
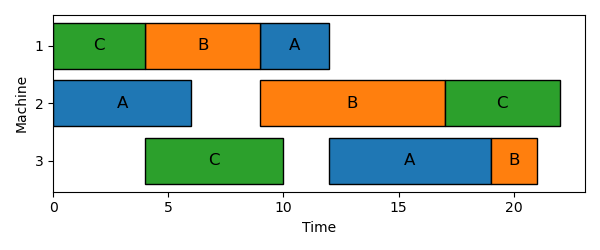
例えば上の表 に対し、
| マシンの順番 | |
|---|---|
| ジョブA | 2 $\rightarrow$ 1 $\rightarrow$ 3 |
| ジョブB | 1 $\rightarrow$ 2 $\rightarrow$ 3 |
| ジョブC | 1 $\rightarrow$ 3 $\rightarrow$ 2 |
と順番が決められたジョブショップ問題について、以下のようにするとメイクスパンが最小($=22$)となる
- フレキシブル問題
上記の問題などに対し、使用するマシンについてのオプションがある場合
(フローショップ問題) $\subset$ (ジョブショップ問題) $\subset$ (フレキシブル問題) の順に汎化される。
現実の問題は、以上のような問題をベースにさらに条件が組み合わさった問題となる。
例
- 1つのジョブが同時に複数のマシンを使用する。(ここでは「マシン」という言葉を使っているが、広く作業者や数の限られた工具などをイメージするとよい)
- 段取り替え
あるマシンは、ジョブ1の後にジョブ2をすぐに実行できるが、ジョブ3の場合は、治具を取り替えたり設定を変更したりするための時間が必要となる。 - マシンがメンテナンスなどで使用できない時間帯が存在する
※ 私見では、これらの用語について業界でもやや混同があるように思われます。
- 「スケジューリング問題」には、この記事では取り扱っていないが、「シフトスケジューリング問題(ナーススケジューリング)」などもある。
- 「ジョブショップスケジューリング問題」について、この記事で取り扱っているような(フローショップやフレキシブルなどを含む)問題全般に対してを述べている場合と、上記のジョブショップ問題に対して述べている場合があるように思われる。
組み合わせ最適化
数学的な観点で最適化問題をいくつかの観点で分類できるが、その中のうちの1つとして、
- 連続値
- 離散値 (組み合わせ)
という分類がある。
最適化問題の例でいうと、栄養問題・輸送問題は連続値、巡回セールスマン問題・ビンパッキング問題については離散値となる。
連続値の場合は、(線形・非線形などにもよるが、)かなり大規模な問題でも効率よく解けるアルゴリズムが多くある一方、組み合わせ問題は、一般には問題を構成する要素の数が多くなってくると組み合わせ爆発を起こし、最適値を求めることが非常に困難になる場合が多い。
スケジューリング問題も組み合わせ問題であり、問題が大きくなると解くのは非常に難しくなる。
ただし、実用上の問題の多くは、必ずしも最適である必要はなく、最適に近い解が求まれば十分な場合も多い。
現状、スケジューリング問題についても、
- 厳密解法
- 近似解法 (メタ解法)
それぞれのアプローチが存在する。
厳密解法
主に分枝限定法をベースに実装されたソルバーが、商用・非商用で企業・研究所などから出されている。一般的なエンジニアはこれらのソルバーを利用するのがよい。
スケジューリング問題の多くの問題設定において、混合整数線形計画(MILP)となる。
ソルバーの例
| 商用 | 非商用 |
|---|---|
| Gurobi CPLEX (IBM) SCOP OptSeq |
SCIP CLP (COIN-OR) GLPK GLOP (google) CP-SAT(google) |
- OptSeqはスケジューリング問題に特化したソルバー、その他は数理最適化問題全般で使用できる。
- SCIPは2022年12月にライセンスが改定され、商用/非商用に関わらず無償となった。
- CP-SATは、充足可能性問題(Wikipedia ja en)を解くソルバー
これらのソルバーのラッパーとなるライブラリも存在する。
例えばpythonだと、
- PuLP
- python-MIP
- google OR-Tools
など
定式化
一般的なエンジニアは、上記のソルバーを利用するにあたっての定式化のスキルを習得する必要がある。
例えば、ジョブショップスケジューリングの場合、
- $n$個のジョブ$J_i (i = 1, 2, \ldots, n)$に、$k_i$個のオペレーション$O_{ij} (j = 1, 2, \dots, k_i)$があり、 $O_{i1} \rightarrow O_{i2} \rightarrow \cdots \rightarrow O_{ik_i}$ の順に実行する必要がある。
- $m$台のマシンがあり、オペレーション$O_{ij}$は1台のマシン$u_{ij} (u_{ij} \in { 1, 2, \ldots, m } )$を使用するものとする。
- オペレーション$O_{ij}$の開始時間、終了時間、処理時間をそれぞれ$s_{ij}, e_{ij}, p_{ij} (\ge 0)$とし、$p_{ij}$はあらかじめ与えられているものとする。
- 最後のジョブが終了する時刻(メイクスパン)が最も早くなるスケジュールを求めたい
という設定が与えられ、制約条件
-
各オペレーションごとの開始時間、終了時間、処理時間の関係
$$ s_{ij} + p_{ij} = e_{ij} $$ -
各ジョブごとの順序に関する制約 ($O_{11} \rightarrow O_{12} \rightarrow \ldots $)
$$ e_{ij} \le s_{ij+1} \quad (i = 1, 2, \ldots, n, j = 1, 2, \ldots, k_i - 1)$$ -
1台のマシンに複数のオペレーションが重ならないようにするための制約
\begin{align} e_{i_1j_1} - s_{i_2j_2} & \le & x_l M \tag{1} \\ e_{i_2j_2} - s_{i_1j_1} & \le & (1 - x_l) M \tag{2} \end{align}ただし、$i_1, j_1, i_2, j_2$ は$u_{i_1j_1} = u_{i_2j_2}, i_1 \le i_2, j_1 < j_2$ となる組み合わせすべてであり、この$L$個の組み合わせそれぞれに対し変数 $x_l = 0 \ or \ 1 \ (l = 1, 2, \dots, L)$ を用意する。
$M$は想定される$s_{ij},e_{ij}$の値よりも十分大きな数とする。 -
メイクスパンを $z$ として、
$$ e_{ik_i} \le z \quad (i = 1, 2, \ldots, N)$$
のもと、 $z$ を最小化する問題を解く。
制約条件のうち、3.はあまり直感的ではないように見えるかもしれません。
2つのオペレーション $(i_1, j_1), (i_2, j_2)$ は処理時間が重なってはいけないものの、どちらが先でなければならないという制約はありません。こうした場合について、$(i_1, j_1)$が先のときと、$(i_2, j_2)$が先のときという場合分けのように考え、これをMILPで解くための ワザ として、$x_l$と$M$を使用しています。
- $x_l = 0$のとき、
- $(1)$ は $e_{i_1j_1} - s_{i_2j_2} \le 0$ となり、2.のように$(i_1, j_1) \rightarrow (i_2, j_2) $のような制約ができる。
- $(2)$は十分大きな$M$のもと、実質的に意味のない式になります。
- $x_l = 1$のときはその逆
問題の種類と例で書いたように、現実の問題はほかにも様々な制約条件があり、それらを数式として落とし込む必要がある。
ファイル形式
多くのソルバーは最適化問題の数式を表現したものとして、lpファイルやmpsファイルといった形式(中身はテキスト)に対応している。
こうしたフォーマットに対応すると、異なるソルバーに対しての互換性が得られる思われるが、統一された規格ではなく、ソルバーごとの独自仕様があることには注意されたい。
近似解法
必ずしも最適解が得られるわけではないが、最適に近い解を可能な限り早く見つける。
- よく知られたアルゴリズム
アルゴリズム個別の内容についてはここでは深くは掘らない。
各プログラミング言語においてライブラリなどもあるが、(筆者の所感として、厳密解法のソルバーを実装するよりは)自前の実装も可能。
解の表現
解の探索に必要となるSAやタブーサーチにおける「状態」、GAにおける「遺伝子」の表現は、さまざまな方法があるようだ。
基本的なものは、オペレーションの順番を何かしらの形で表現して、その順番で各オペレーションごとに可能な限り早い時間に置いていくというような手順でその表現に対応するスケジュールを作成する。
例えば、問題の種類と例のジョブショップ問題で示した最適解は、
-
各マシンごとにジョブを順番に並べる。
マシン1 マシン2 マシン3 C B A A B C C A B 最初の3文字はマシン1における各ジョブの順、次の3文字は...となる。
-
各ジョブの番号をそのジョブが使用するマシン数分だけ繰り返して1列に並べる
C A C B A A B C B - 1文字目「C」: ジョブCが最初に使うマシン1
マシン1にオペレーションはまだないので、時刻$0$に置く - 2文字目「A」: ジョブAが最初に使うマシン2
マシン2にオペレーションはまだないので、時刻$0$に置く - 3文字目「C」: ジョブCが2番目に使うマシン3
マシン3にオペレーションはないが、1.の後に実行されるので時刻$4$に置く - 4文字目「B」: ジョブBが最初に使うマシン1
1.のオペレーションがあるので、その後の時刻$4$に置く
...(同じことを最後まで続ける)
- 1文字目「C」: ジョブCが最初に使うマシン1
-
各マシンごとに、同じマシンを使用する2つのジョブの前後関係をバイナリ(0, 1)で表現する。
マシン1 マシン2 マシン3 A $\rightarrow$ B A $\rightarrow$ C B$\rightarrow$ C A $\rightarrow$ B A $\rightarrow$ C B$\rightarrow$ C A $\rightarrow$ B A $\rightarrow$ C B$\rightarrow$ C 0 0 0 1 1 1 1 0 0 それぞれ表の2行目に書いた順番の場合を1、そうでない場合を0とする。
それぞれ、
- 複数の表現が1つの同じスケジュールを表す。
- 実行不可能な表現が現れる。
といったことが起きる。
ある表現から別の表現に移す際に、多くのアルゴリズムでは、元のものと似たものになることが望ましいが、そうした遷移の方向には工夫が必要。
GAの場合だと、交叉の方法についても考える必要がある(巡回セールスマン問題で使うような順列コーディングの発展形として考える)。
ベンチマーク問題 (+実際に解いてみる)
ソルバーのパフォーマンスを測るためのベンチマーク問題が公開されている。もとはいくつかの論文から出されているようだが、それらをまとめたサイトがいくつかある。
解に関する情報は古い場合があることに注意
google OR tools のCP-SATソルバーを用いて、定式化と同じ式をたて、ベンチマーク問題を解いた。
ふつうの(市販されている程度の)デスクトップ型PCでどれくらいのパフォーマンスが出るのか試してみた。
- スペック
| OS | Windows 11 Pro |
| CPU | Intel(R) Core(TM) i9-9900K CPU @ 3.60GHz 8コア |
| RAM | 32GB |
google OR tools のバージョン ... 9.7.2996
-
la40 (15 jobs x 15 machines)
- 知られている最適値 1222

数秒で後に最適と判明する解に到達した。
※ 探索途中の解も出力することができる。
その解が最適と判明するまでには2~3分程度かかった
※ 実行のたびに途中の挙動は変化する。
かつては「10 Tough Problem」と呼ばれるもののうちの1つだったようです(Wikipedia)。 -
ta21 (20 jobs x 20 machines)
- 知られている最適値 1642
-
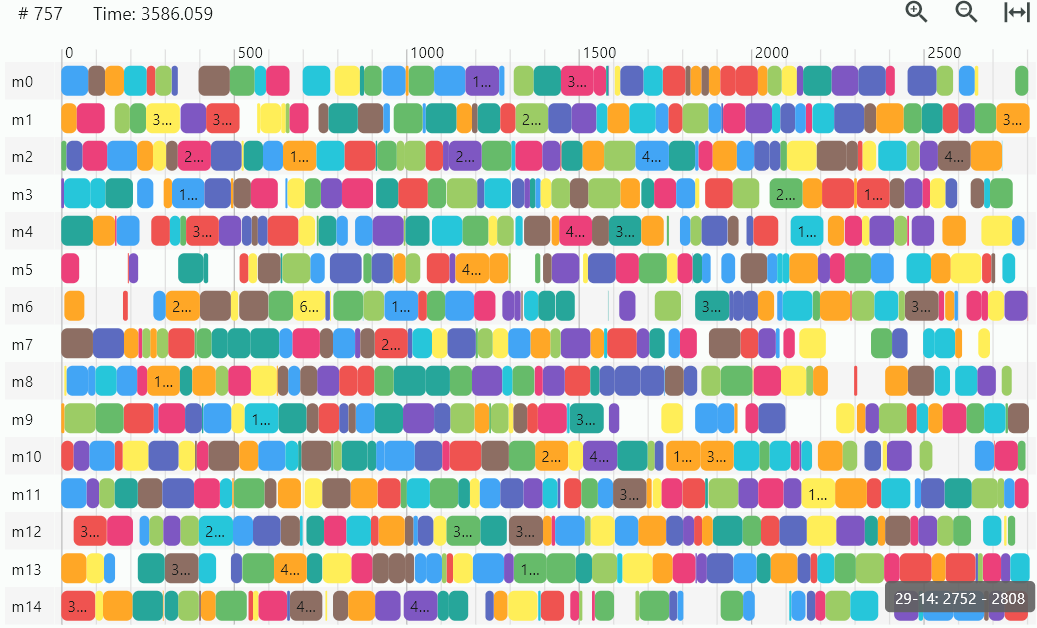
ta51 (50 jobs x 15 machines)
- 知られている最適値 2760
最後に
古典的な手法についてのまとめになりましたが、GPUであったり、量子コンピューターを使ったりするような手法も今後調べられたらと思います。