この記事はDP初心者向けになります。
そもそもDPって何って人は、けんちょんさんの記事をどうぞ!
最近DPの勉強をはじめて、
DPの次元を減らすテクニック
に非常に感動したので記事にしてみます!!!
以下の2問を実際に解きながら簡単に解説したいと思います。
-
TDPC A - コンテスト
→DPを2次元から1次元へ -
ABC 015 D - 高橋くんの苦悩
→DPを3次元から2次元へ
TDPC A - コンテスト
典型的な部分和問題です。
今回の問題はNのMAXが100
→bit全探索とかだと計算量的に無理なのでDPで考える。
DP:2次元Ver
普通に、DPを2次元として解くと、こんな感じー
※点数のパターンは0〜100点ではなく、0〜MAX10000(100*100)点であることに注意
import itertools,sys
def I(): return int(sys.stdin.readline().rstrip())
def LI(): return list(map(int,sys.stdin.readline().rstrip().split()))
#############################
N = I()
p = LI()
dp = [[0]*10001 for _ in range(N+1)] #0:その点数存在しない、1:その点数存在する
dp[0][0] = 1
for i,j in itertools.product(range(1,N+1),range(10001)):
pi = p[i-1]
if j-pi>=0:
dp[i][j] = max(dp[i][j],dp[i-1][j-pi]) #選んだ場合
dp[i][j] = max(dp[i][j],dp[i-1][j]) #選ばなかった場合
print(sum(dp[-1])) #1の数字の個数を出力
DP:1次元Ver
これをDP1次元にするにはこうする!
import itertools,sys
def I(): return int(sys.stdin.readline().rstrip())
def LI(): return list(map(int,sys.stdin.readline().rstrip().split()))
#############################
N = I()
p = LI()
dp = [0]*10001 #0:その点数存在しない、1:その点数存在する
dp[0] = 1
for i,j in itertools.product(range(1,N+1),range(10001)[::-1]):
pi = p[i-1]
if j-pi>=0:
dp[j] = max(dp[j],dp[j-pi]) #選んだ場合
#dp[j] = max(dp[j],dp[j]) #選ばなかった場合→不要
print(sum(dp)) #1の数字の個数を出力
ポイントはここ!!!
range(10001)[::-1]
※range(10000,-1,-1)でも可
逆からループを回すことで、dpを使い回すことができる!!!!!
これがテクニック!!!!!
もしdpを使いまわしながら、順番にループを回すと
例えばp=2点の場合に、
dp = [1,0,1,0,1,0,1,0,1 ・・・]
と4点、6点、8点・・・も存在することになってしまう・・・
なぜなら、
dp[j] = max(dp[j],dp[j-pi])
2点が1なので4点も1になる。。。
4点が1なので、6点も1になる。。。
・・・
しかし、逆からループさせると・・・
dp = [1,0,1,0,0,0,0,0,0 ・・・]
dp[j] = max(dp[j],dp[j-pi])
・・・
4点が0なので、6点も0になる!
2点が0なので、4点も0になる!
0点が1なので、2点は1になる!!!
ということでdpを使いまわしながら、正しい結果を得られることができる!!!!!!!!!
→dpの次元を2次元から1次元に落とすことができる!!!!!!!!!!
dpの次元が下がることで、
頭で考える量が減ってめちゃくちゃ嬉しい!
この感動伝わるかな〜
伝わってくれ〜
感動をより実感してもらうためにもう一問!!!
ABC 015 D - 高橋くんの苦悩
Difficulty:1388の水色問題!
ナップサックDPに変数が1つ増えた、少しだけ発展的な問題。
DP:3次元Ver
3次元でDPを考えたらできなくもないけど、頭がパンクしそう・・・・・・・・・・
import itertools,sys
def I(): return int(sys.stdin.readline().rstrip())
def LI(): return list(map(int,sys.stdin.readline().rstrip().split()))
#############################
W = I()
N,K = LI()
AB = [LI() for _ in range(N)]
dp = [[[0]*(W+1) for _ in range(K+1)] for _ in range(N)] #k枚使った時の重要度の最大値を保持
for i,k,w in itertools.product(range(N),range(1,K+1),range(W+1)):
A,B = AB[i]
if w-A>=0:
dp[i][k][w] = max(dp[i][k][w],dp[i-1][k-1][w-A]+B)
dp[i][k][w] = max(dp[i][k][w],dp[i-1][k][w])
print(dp[-1][-1][-1])
しかしこれではPythonだと計算量的にTLE、PyPyだとMLE
オワタ・・・
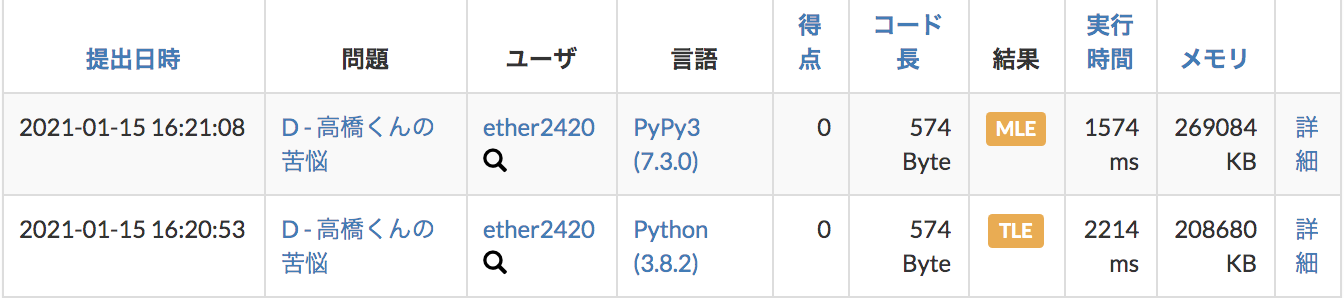
DP:2次元Ver
ここで!
さきほどの次元削減テクニックをつかって、
なんとかDPを使えまわすことができないか!
と考えてやってみると・・・
どうやら2次元にできそう・・・!
import itertools,sys
def I(): return int(sys.stdin.readline().rstrip())
def LI(): return list(map(int,sys.stdin.readline().rstrip().split()))
#############################
W = I()
N,K = LI()
AB = [LI() for _ in range(N)]
dp = [[0]*(W+1) for _ in range(K+1)] #k枚使った時の重要度の最大値を保持
for i,k,w in itertools.product(range(N),range(1,K+1)[::-1],range(W+1)[::-1]):
A,B = AB[i]
if w-A>=0:
dp[k][w] = max(dp[k][w],dp[k-1][w-A]+B)
#dp[k][w] = max(dp[k][w],dp[k][w])
print(dp[-1][-1])
ポイントはここ!!!
range(1,K+1)[::-1],range(W+1)[::-1]
逆からループで、DPを使いまわせる!!!
気になる結果は・・・
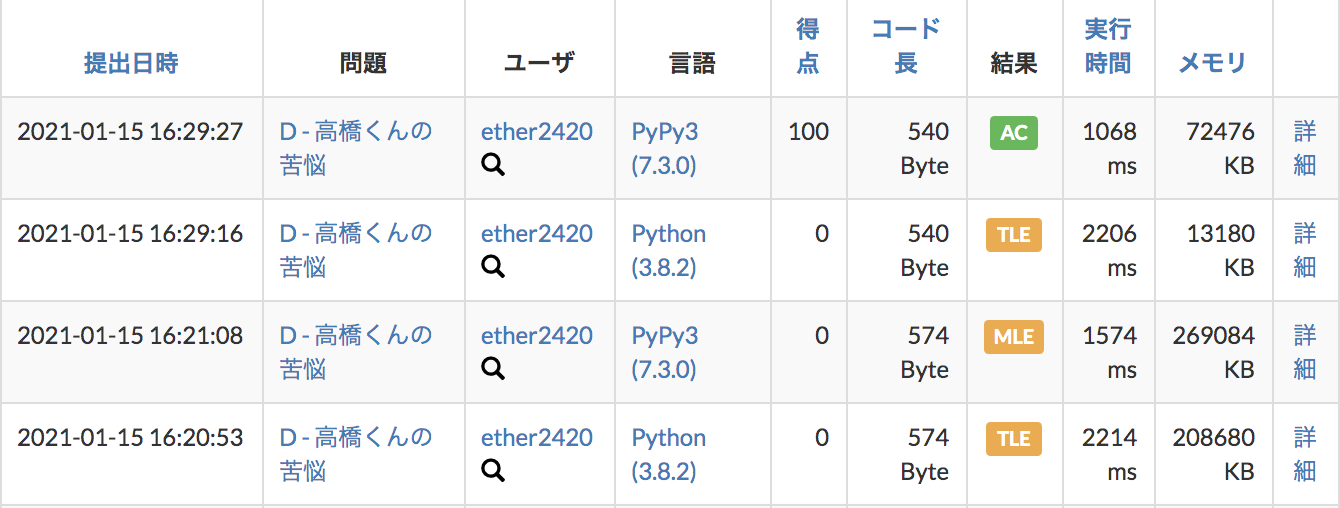
あいかわらず、PythonはTLEでしたがw(次元削減したからといって計算量が削減されるわけではなかったw)
PyPyで無事ACになりました〜!!!
今後DP問題が出た時に、次元が2次元以上になりそうだったら、
この次元削減テクニック使えないか考えてみよう〜
おわり!!!