【高等学校情報科 情報Ⅰ】教員研修用教材：データの形式と可視化（python）

はじめに

今回は文部科学省のページで公開されている情報Ⅰの教員研修用教材の「第4章情報通信ネットワークとデータの活用・巻末」内の「データの形式と可視化」について、pythonでの実装と及び若干の補足考察をしていきたいと思います。

教材

高等学校情報科「情報Ⅰ」教員研修用教材（本編）：文部科学省
第4章情報通信ネットワークとデータの活用・巻末 （PDF:10284KB）

環境

• ipython
• Colaboratory - Google Colab

今回やること

教材の学習24「データの形式と可視化」(p202-)内のRで示されている実装例をpythonに書き換えていきたいと思います。

前提

教材には

総務省統計局の身体測定のサンプルデータから，箱ひげ図とヴァイオリンプロットを作成した。

と書いてあるが、Rで読み込んでいるデータファイルが50m走の男女の結果っぽいので、こちらで適当に用意した以下のデータを使用しました。
high_male_data.csv

また、後半のpython実装版にて使用している"diamonds.csv"はkaggleのサイト上のものを使われていただきました。
Diamonds - Kaggle

質的データとその種類

箱ひげ図とヴァイオリンプロット

python実装版のソースコード

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

gen_50 = pd.read_csv('/content/gen_50.csv')

plt.subplots_adjust(wspace=0.5)

sns.boxplot(x = 'gender', y = 'run50m', data = gen_50)
plt.show()
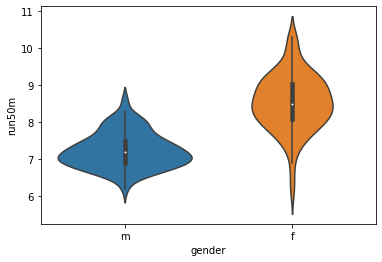
sns.violinplot(x = "gender", y = "run50m", data = gen_50)
plt.show()

ヴァイオリンプロットの描画にseabornモジュールを使ったので、箱ひげ図の描画にもseabornモジュールを使いました。

python実装版の出力結果

[参考]R実装版のソースコード(教材より)

library( ggplot2 )
# データの読み込み
gen_50 <- read.csv("gen_50.csv")
boxplot(run50m~gender, data=gen_50)
ggplot(data=gen_50, aes(x=gender, y=run50m, color=gender)) + geom_violin()

ちなみに、実際の教材に書かれているソースコードは以下のようになっております。

ここにバグがあるのでご注意ください。
誤：boxplot(run50m~gender.data=gen_50)
正：boxplot(run50m~gender,data=gen_50)

[参考]R実装版の出力結果

ヒストグラムと散布図と箱ひげ図

　データの可視化は何のために行うのだろうか。可視化することによって，問題を発見することができ，それに対して詳細な分析や解釈，解決策を考えることができるからである。ここでは，統計解析ソフトウェア R の ggplot2 というパッケージに含まれている diamonds サンプルデータを用いて説明しよう。このデータは，実際に米国で流通したダイアモンドのカラット，カット，透明度，大きさ，価格などを含んだ数万件の大きなデータである。

python実装版のソースコード

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

df = pd.read_csv('/content/diamonds.csv')

df_carat_lt3 = df[df['carat'] < 3]

# x軸にcarat、y軸にcount
plt.xlabel('carat')
plt.ylabel('count')

# ヒストグラムを描画する
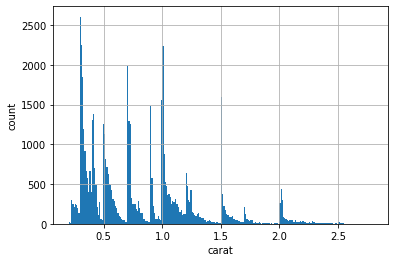
df_carat_lt3['carat'].hist(bins=250)
plt.show()

# 散布図を描画
df_carat_lt3.plot.scatter(x = 'carat', y = 'price')
plt.show()

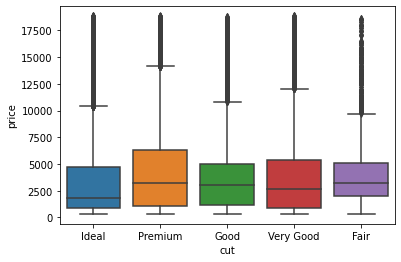
sns.boxplot(x = 'cut', y = 'price', data = df_carat_lt3)
plt.show()

python実装版の出力結果

カラット数が大きくなるほど、価格もあがることがわかる。

最後の図のx軸の順番があまり良い形ではないですがカットの質の順番はIdeal>Premium>Very Good>Good>Fairです。

コメント

教材には、以下のように書かれています。

これは不思議な現象に見えるだろう。カットの質が上がるほど，価格が下がっている。色や透明度の高さなどでも同様の逆転現象が起こる。ヒントは「交絡因子」である。交絡因子とは，対象としている 2変数と相互に相関の高い隠れた変数（因子）のことである。

これまでの結果からカラット数が高いほど価格も高いことがわかってます。
ここから考えられるのは、カラット数の大きいダイヤモンドは、カットの質が悪いものが多いということが推測されます。
（すなわちカットの質が上がるほど価格が下がっているのは、交絡因子であるカラット数等による影響があるのではないかということです）

python実装版のソースコード(cut vs carat)

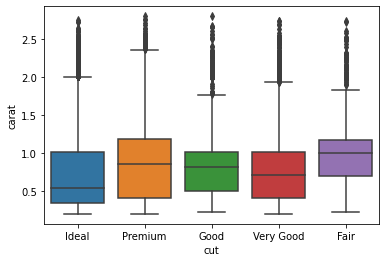
sns.boxplot(x = 'cut', y = 'carat', data = df_carat_lt3)
plt.show()

python実装版の出力結果(cut vs carat)

想定した通りであり、特に中央値をみるとカットの質が一番高いIdealのカラット数は一番低くカットの質が一番低いFairのカラット数は一番低いことがわかりました。　

このダイアモンドに関するデータ分析でもっと詳しく分析したものが見たい場合は、以下のサイト等を確認すると良いと思います。
https://www.kaggle.com/fuzzywizard/diamonds-in-depth-analysis

ダイアモンドのカットの質について(補足)

• カットの質が上がるほど、カラットあたりのコストが増加する。
• カラット数の大きいダイヤモンド原石はより良い対称性とプロポーションを達成するためにより多くの材料が必要となり大きな無駄ができてしまう。

[参考]R実装版のソースコード(教材より)

library(ggplot2)
diamonds

smaller <- diamonds %>% filter(carat < 3)
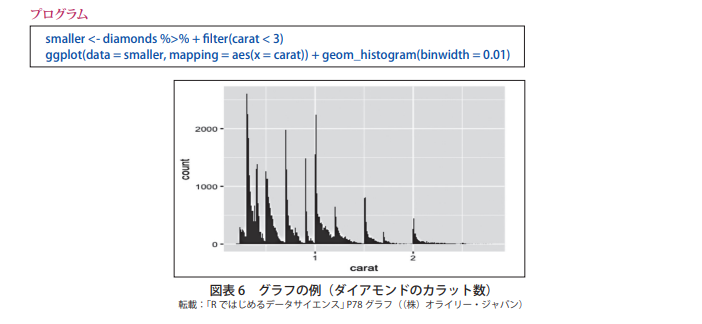
ggplot(data = smaller, mapping = aes(x = carat)) + geom_histogram(binwidth = 0.01)

ggplot(data = diamonds) + geom_point(mapping = aes(x = carat, y = price))

ggplot(diamonds, aes(cut, price)) + geom_boxplot()

ちなみに、実際の教材に書かれているソースコードは以下のようになっております。

ここにバグがあるのでご注意ください。
誤：smaller <- diamonds %>% + filter(carat < 3)
正：smaller <- diamonds %>% filter(carat < 3)

[参考]R実装版の出力結果

A tibble: 53940 × 10
carat   cut color   clarity depth   table   price   x   y   z
<dbl>   <ord>   <ord>   <ord>   <dbl>   <dbl>   <int>   <dbl>   <dbl>   <dbl>
0.23    Ideal   E   SI2 61.5    55  326 3.95    3.98    2.43
0.21    Premium E   SI1 59.8    61  326 3.89    3.84    2.31
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
（省略）
⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
0.86    Premium H   SI2 61.0    58  2757    6.15    6.12    3.74
0.75    Ideal   D   SI2 62.2    55  2757    5.83    5.87    3.64

ソースコード

python版
https://gist.github.com/ereyester/68b781bd6668005c157b300c5bf22905

R版
https://gist.github.com/ereyester/737207c4c99556850950c5b5a49dbfcc