Pythonによる移動通信シミュレーション 受信電力の変動（見通し外NLoS環境）

はじめに

携帯電話などの通信では以下のよう理由から受信電力が常に変動します．

• 携帯電話など端末自体が移動する
• 都市部では電波は建造物等で反射するため，受信側ではあらゆる角度から複数の電波（素波）が受信される

本記事では，資料[1]等を参考に，このような移動通信環境の基本をまとめてみることにします．具体的には，見通し外(NLoS; Non Line of Sight)環境のマルチパス波が存在する状況で，端末が移動する場合の受信電力の特性をPythonによりシミュレーションしてみます．

定式化

本記事では，いわゆる送受信アンテナが1つずつの場合のSISO（Single Input Single Output）において，受信側の端末が見通し外（NLoS）のマルチパス環境で移動する状況を想定します．なお，見通し外NLoS環境は，送受アンテナが互いに見つめあってない環境です．

送信・受信信号の表現

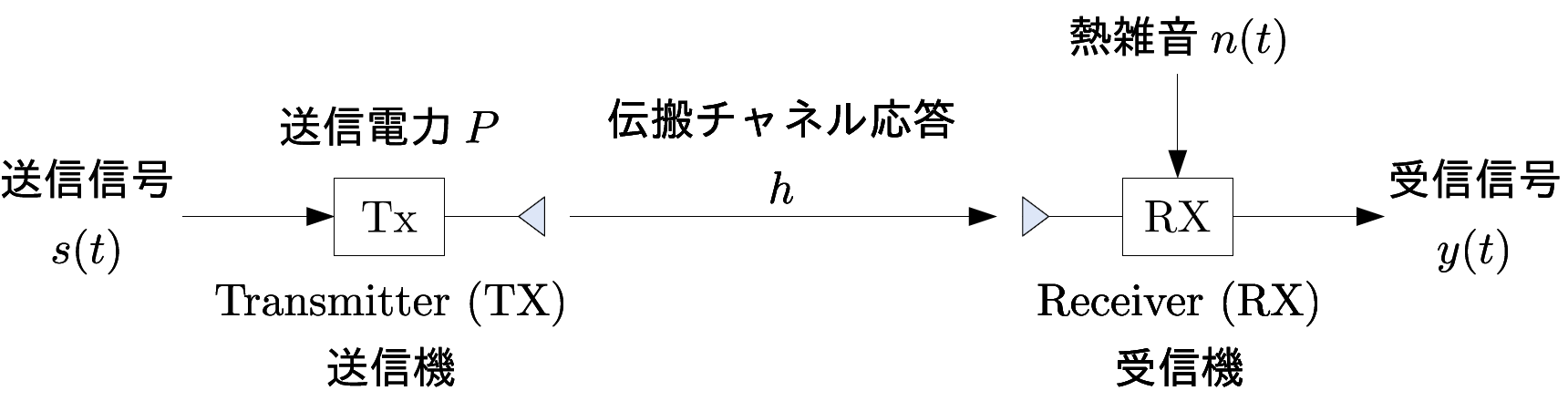
図に示すようなシンプルな送受アンテナが1つ存在する状況を考えます．受信側における信号$y(t)$は，送信信号$s(t)$と送信電力$P$により次のように表現されます．

y(t) = \sqrt{P} h s(t) + n(t)

ここに，$h$は伝搬チャネル応答(複素数)であり，端末の移動やマルチパスによる信号$s(t)$の振幅変動の様子を示しています（後述）．また，$n(t)$は熱雑音(複素数)であり，いわゆる加法性白色ガウス雑音(AWGN; Additive White Gaussian Noise)です(詳細は補足参照)．

伝搬チャネル応答の表現

移動通信の伝搬環境では，1) 複数の信号（マルチパス）が様々な方向から到来し，2) 端末が移動します．これらを表現するのが前述の伝搬チャネル応答$h$となります．以下，1)と2)の状況を順に定式化していきます．

1) マルチパスの表現

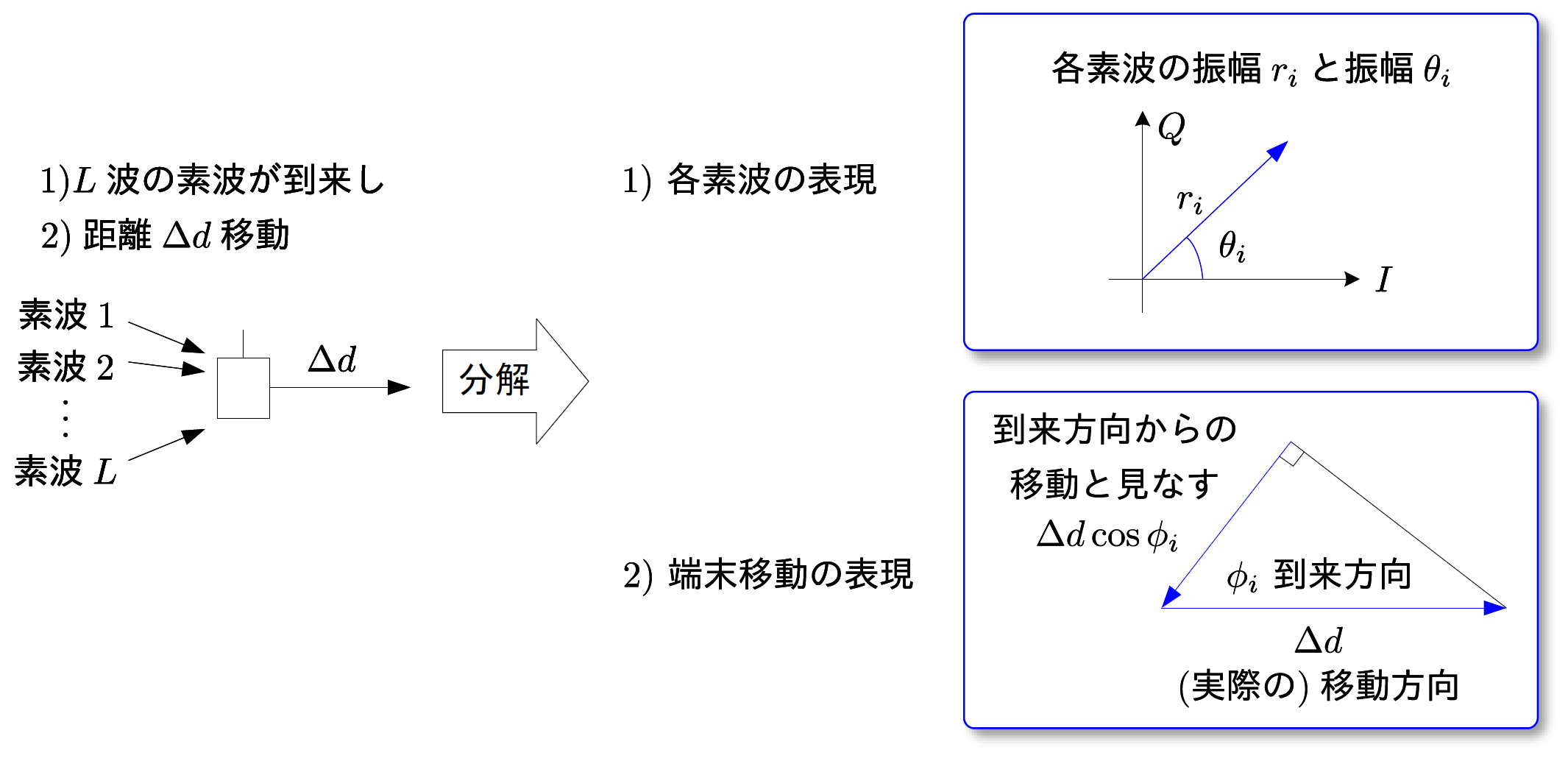
ある端末で受信する素波（ある経路(パス)を通ってきた1本の電波）の数を$L$とします．各素波の振幅を$r_i$，位相を$\theta_i$とするとき，(端末の移動を考慮しない)伝搬チャネル応答は次のように与えらえます．

h = \cfrac{1}{\sqrt{L}} \sum_{i=1}^L r_i \exp(j \theta_i)

ここで，$j$は虚数単位です．

2) マルチパス+端末移動の表現

上記の1)の環境に加えて端末が移動する環境を考えます．今，移動距離を$\Delta d$とし，ある素波の到来角度を$\phi_i$とします．このとき，状況をシンプルにするために，端末が到来方向に向かって移動していると見なすと，等価的な移動距離は$\Delta d \cos\phi_i$となります．

ところで，空間的に位相が変動する様子は波数によって表現されます．波数は$k=2\pi/\lambda_0$ [rad/m]で与えられます($\lambda_0$は自由空間での波長)．単位を見てわかるように，単位距離あたりの位相変化を表しています．今，移動距離が$\Delta d \cos\phi_i$ですから端末の移動に伴う空間的な位相変化は$(2\pi/\lambda_0 \cdot \Delta d \cos \phi_i)$となりますよね．

以上より端末の移動まで考慮した伝搬チャネル応答$h'$が次のように与えらえます．

h'
= h \cdot \exp \left( j \cfrac{2\pi}{\lambda_0} \Delta d \cos\phi_i \right)
= \cfrac{1}{\sqrt{L}} \sum_{i=1}^L r_i \exp(j \theta_i) \exp \left( j \cfrac{2\pi}{\lambda_0} \Delta d \cos\phi_i \right)

相対受信電力のPythonシミュレーション

伝搬チャネル応答$h'$がどのようなふるまいをするのかを，Pythonによる数値計算で調べてみます．シミュレーションでは，以下の表の条件を与え，端末を移動させた場合の相対信号電力$|h'|^2$の距離に対する変動特性を調べます．

パラメータ	設定値
素波の数	2,32
各素波の振幅$r_i$	1
各素波の位相$\theta_i$	一様乱数[0,2$\pi$]
各素波の到来角$\phi_i$	一様乱数[0,2$\pi$]
信号周波数	2 GHz

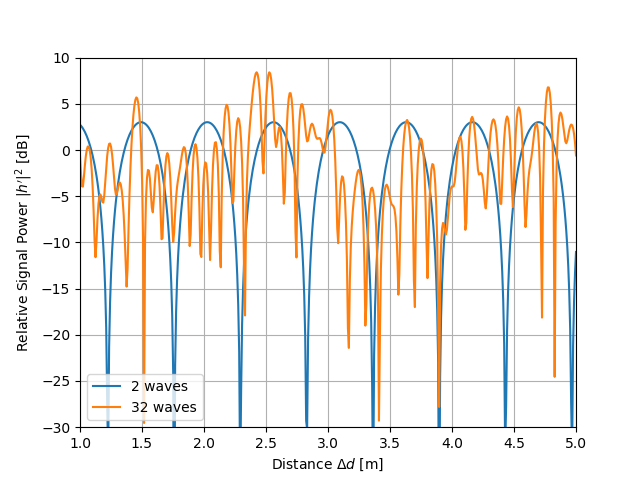
下図は，シミュレーション結果の一例です．同図に示すように，1) 端末の場所により受信電力が大きく変化しています．2) 素波の数$L$を増やしていくと，受信電力の変動が移動距離に対して複雑になっていることも分かります．

import numpy as np
import matplotlib.pyplot as plt

d = np.linspace(1, 5, 512)  # 移動距離
l = [2, 32]                 # 検討する素波の数
f = 2*(10**9)               # 周波数
lam = 3*(10**8)/f           # 波長
k = 2*np.pi/lam             # 波数

# 素波の数
for i in range(len(l)):
    h = 0
    # h= sum_{i=1}^{l} r_i exp(j theta_i) 素波の数だけ合成
    for j in range(l[i]):
        # 振幅
        r = 1
        # 位相θと到来角φ ([0,2π]の一様乱数)
        theta = np.random.uniform(low=0.0, high=2*np.pi)
        phi = np.random.uniform(low=0.0, high=2*np.pi)
        isou = theta + k*d*np.cos(phi)
        h += r*np.exp(1j*isou)
    # h'の計算終了
    h = h/np.sqrt(l[i])
    # |h'|^2をdBに換算
    h = 10*np.log10(abs(h)*abs(h))

    # プロット
    plt.plot(d, h, label=str(l[i])+" waves")


# グラフの体裁
plt.legend()
plt.ylim(-30, 10)
plt.xlim(min(d), max(d))
plt.xlabel("Distance $\Delta d$ [m]")
plt.ylabel("Relative Signal Power $|h'|^2$ [dB]")
plt.grid()
plt.show()

(補足)加法性白色ガウス雑音（AWGN）

無線通信システムにおける雑音は，送受信機やアンテナなどのシステム内部で発生する内部雑音と，システム外部で発生する外部雑音に大別されます．内部雑音は外部雑音に比べて雑音電力が大きく，時間的に連続的な影響を与えるため，無線通信システムでは支配的な雑音となります．
ところで，雑音の性質を統計的に評価する際，時間と周波数の側面から評価します．内部雑音は，時間波形がガウス雑音，周波数波形が白色雑音となります．また，内部雑音は，信号の振幅に加算されることから，加法性雑音と呼ばれます．これらの特徴を総合して，内部雑音のことを加法性白色雑音（AWGN; Additive White Gaussian Noise）と呼びます [2]．

参考

[1]西森，マルチユーザMIMOの基礎，コロナ社，2014年．
[2]高畑ほか，ディジタル無線通信入門，培風館，2005年．