はじめに
多くの教科書やサイトでは,冒頭で複素電力$P_c$を
\begin{equation}
P_c=I_EV_E^* \\
但し,I_E:(フェーザ)電流,V_E:(フェーザ)電圧
\end{equation}
「とする」と書いてあります.**なぜ?**でしょう.その答えを書籍やネットで調べてみると,
- 複素共役を使わないと,意味のない表示になる→なぜ意味がない?どのように意味がない?
- 有効電力等の表示になるから都合がよい→後付けの理由に過ぎない.逆になぜ複素共役を使ったら有効電力等になるのか?
といった疑問が出てきて,どうしても納得いきませんでした(私の勉強不足が原因かもしれません..).そこで,ここでは実電力と見比べながら複素電力に複素共役を使う理由について説明します.
実電圧・実電流を用いた平均電力
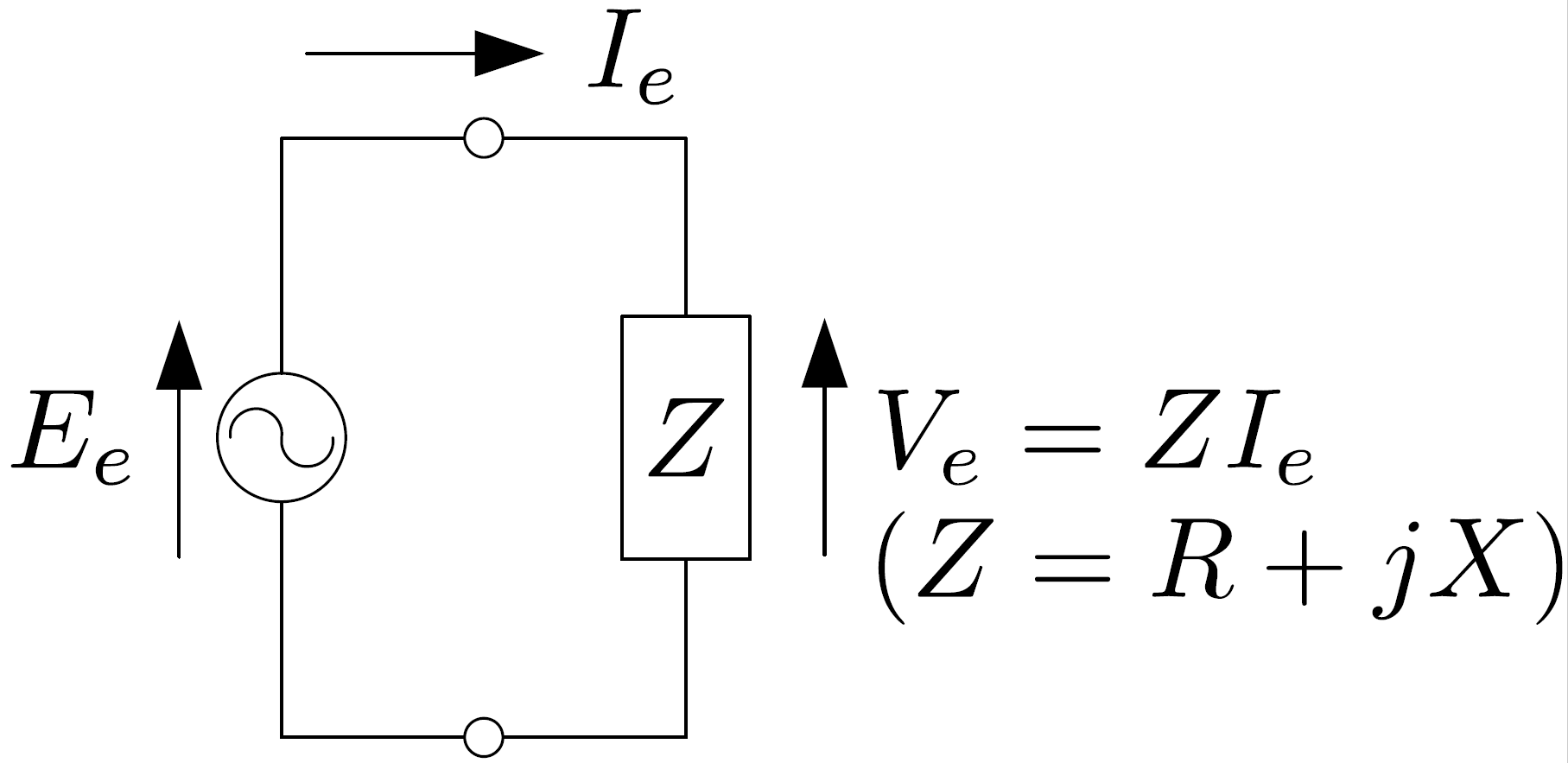
図の様なインピーダンス$Z$の負荷が接続された回路を考えます."$Z$の両端の複素電圧及び複素電流$V_e$,$I_e$を次の様に表現します."
\begin{align}
&Z=R+jX=|Z|e^{j\theta}=|Z|(\cos{\theta}+j\sin{\theta}) \\
&V_e=|E_e|e^{j\theta_E} \\
&I_e=|I_e|e^{j\theta_I}
\end{align}
ここで$E_e$,$I_e$は複素電圧・電流の実効値で,電圧・電流の最大振幅$E_m $,$I_m$に対して
\begin{align}
E_m&=\sqrt{2}E_e \\
I_m&=\sqrt{2}I_e
\end{align}
の関係がありますね.また,$\theta_E$と$\theta_I$は電圧・電流の初期位相を表します.最初の複素電圧・電流の式をもう少し変形させてください..
\begin{align}
V_e&=|E_e|e^{j\theta_E} \\
I_e&=|I_e|e^{j\theta_I}=\frac{V_e}{Z}=\frac{|E_e|e^{j\theta_E}}{|Z|e^{j\theta}}=
\left|\frac{E_e}{Z}\right|e^{j(\theta_E-\theta)}
\end{align}
ですね.下の電流に関する式に注目すると
\begin{equation}
|I_e|=\left|\frac{E_e}{Z}\right|,
\theta_I=\theta_E-\theta
\end{equation}
という関係があります.
複素電圧・電流から実電圧・電流への書き換え
実電圧$e(t)$と先ほどの複素電圧$E_e$の間には次のような関係があります.
\begin{align}
e(t)&=|E_m|e^{j(\omega t+\theta_E)}=\sqrt{2}|E_e|\cos{(\omega t+\theta_E)} \\
&=Re[\sqrt{2}|E_e|e^{j(\omega t+\theta_E)}]
\end{align}
これを参考にすると,$V_e$と$I_e$の式は実電流を用いて次のように表現できます.
\begin{align}
e(t)&=Re[\sqrt{2}|E_e|e^{j(\omega t+\theta_E)}]=\sqrt{2}|E_e|\cos{(\omega t + \theta_E)} \\
i(t)&=Re[\sqrt{2}|I_e|e^{j(\omega t+\theta_I)}]=\sqrt{2}|E_e|\cos{(\omega t + \theta_I)}
\end{align}
電流の初期位相$\theta_I$は先ほどのべたように$\theta_I=\theta_E-\theta$の関係がありますから,$i(t)$はさらに書き直されて
\begin{align}
i(t)=\sqrt{2}|E_e|\cos{(\omega t + \theta_E-\theta)}
\end{align}
平均電力の計算
改めて,実電圧・電流$e(t)$と$i(t)$を掲示すると次のようになります.
\begin{align}
e(t)&=\sqrt{2}|E_e|\cos{(\omega t + \theta_E)} \\
i(t)&=\sqrt{2}|E_e|\cos{(\omega t + \theta_E-\theta)}
\end{align}
これらを用いて平均電力$P$を計算していきます.そのためにまず,**瞬時電力$p(t)$**を計算します.交流では電圧・電流が時々刻々と変動し,ある時刻$t$における電力のことを瞬時電力と呼び,次のように表現できます.
\begin{align}
p(t)=e(t)i(t)
\end{align}
直流の電力の式と同じですね"(-""-)"!これを用いると,
\begin{align}
p(t)&=e(t)i(t)
=\sqrt{2}|E_e|\cos{(\omega t + \theta_E)}\cdot\sqrt{2}|E_e|\cos{(\omega t + \theta_E-\theta)} \\
&=2|E_eI_e|\cos{(\omega t + \theta_E)}\cos{(\omega t + \theta_E-\theta)} \\
&=|E_eI_e|\{\cos{(2\omega t+2\theta_E+\theta)}+\cos{\theta}\}
\end{align}
途中の計算$\cos{()}*\cos{()}$の部分は加法定理を用いると,
\begin{equation}
\cos{\alpha}\cos{\beta}=\frac{1}{2}\{\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}\}
\end{equation}
となります.さて,瞬時電力が時々刻々と変動する電力を表しますが,平均電力$P$は瞬時電力を1周期$T$にわたって足し合わせて,1周期$T$で割ることで求められます.したがって,
\begin{align}
P&=\frac{1}{T}\int^{T}_{0} p(t)dt=
\frac{|E_eI_e|}{T} \int^{T}_{0} \{\cos{(2\omega t+2\theta_E+\theta)}+\cos{\theta}\}dt \\
&=\frac{|E_eI_e|}{T} \left[\frac{1}{2\omega}\sin{(2\omega t+2\theta_E+\theta)}+\cos{\theta}\cdot t\right]^T_0 \\
&=\frac{|E_eI_e|}{T} \left[
\left\{\frac{1}{2\omega}\sin{(2\omega T+2\theta_E+\theta)}+\cos{\theta}\cdot T\right\}-
\left\{\frac{1}{2\omega}\sin{(2\omega \cdot 0+2\theta_E+\theta)}+\cos{\theta}\cdot 0\right\}
\right]
\end{align}
ここで,$\omega =2 \pi / T$ですので上の式の第1項$(1/2\omega)\sin{(2\omega \cdot T+2\theta_E+\theta)}$は書き換えられて
\begin{align}
\frac{1}{2\omega}\sin{(2\omega T+2\theta_E+\theta)}
=\frac{1}{2\omega}\sin{(2\pi+2\theta_E+\theta)}
=\frac{1}{2\omega}\sin{(2\theta_E+\theta)}
\end{align}
となります.改めて,平均電力$P$は
\begin{align}
P&=\frac{|E_eI_e|}{T} \left[
\left\{\frac{1}{2\omega}\sin{(2\theta_E+\theta)}+\cos{\theta}\cdot T\right\}-
\frac{1}{2\omega}\sin{(2\theta_E+\theta)}
\right] \\
&=\frac{|E_eI_e|}{T} \cos{\theta} \cdot T \\
&=|E_eI_e|\cos{\theta}
\end{align}
なります.ようやく,平均電力が姿を現しました.
複素電力
さて,では本丸に乗り込みましょう.複素電力$P_{fake}$をあえて複素共役を用いずに次の様に定義します.
\begin{equation}
P_{fake}=V_eI_e
\end{equation}
そして,この定義に従って$P_{fake}$を計算していきます.$V_e$と$I_e$は先ほどの式を用います.
\begin{align}
P_{fake}&=V_eI_e \\
&=|E_e|e^{j\theta_E}|I_e|e^{j\theta_I} \\
&=|E_e|e^{j\theta_E}|I_e|e^{j(\theta_E-\theta)} \\
&=|E_eI_e|e^{j(2\theta_E-\theta)} \\
&=|E_eI_e|\{\cos{(2\theta_E-\theta)}+j\sin{(2\theta_E-\theta)}\}
\end{align}
あれ,実電圧・電流を用いて算出した計算結果$P=|E_eI_e|\cos{\theta}$と位相が合わないし,$\sin{()}$の項が出てきますね...
では,平均電力を複素共役を用いて表現すると,
\begin{align}
P_{c}&=V_eI_e^* \\ \notag
&=|E_e|e^{j\theta_E}|I_e|e^{-j\theta_I} \\
&=|E_e|e^{j\theta_E}|I_e|e^{-j(\theta_E-\theta)} \\
&=|E_eI_e|e^{j\theta} \\
&=|E_eI_e|(\cos{\theta}+j\sin{\theta})
\end{align}
先ほどの計算結果$|E_eI_e|\cos{\theta}$と位相がそろいました!!では,$\sin{()}$の項はいったい何でしょうか?
ようやく有効電力・皮相電力・無効電力
改めて,実電圧・電流を用いて計算した平均電力$P$と複素電力$P_c$を見比べると,
\begin{align}
P&=|E_eI_e|\cos{\theta} \\
P_c&=|E_eI_e|(\cos{\theta}+j\sin{\theta})
\end{align}
となります.実は複素電力の計算では,実(際の)電圧・電流では出てこない無効な項が出てきます.この無効な項のことを無効電力と呼びます.一方で実(際の)電力でも出てくる項の事を有効電力と呼びます.また,先ほどの複素共役を用いない複素電力$P_{fake}$は見かけ上の電力なので皮相電力と呼びます.
\begin{align}
複素電力&:P_c=V_eI_e^* \\
有効電力&:P_e=Re[P_c]=|V_eI_e|\cos{\theta}\\
無効電力&:P_s=Im[P_c]=|V_eI_e|\sin{\theta}\\
皮相電力&:|P_{fake}|=|V_eI_e|
\end{align}
なお,有効電力の$\cos{\theta}$を力率と呼びます.