PythonによるFFT

はじめに

この記事では，Pythonを使ったフーリエ変換をまとめました．書籍を使ってフーリエ変換を学習した後に，プログラムに実装しようとするとハマるところが(個人的に)ありました．具体的には，以下の点を重点的にまとめています．

• サンプリング周波数
• 離散フーリエ変換のサンプルポイント数
• 配列のインデックスと周波数の関係
• 配列の構造

コンピュータで扱うフーリエ変換

コンピュータで数値を扱うには飛び飛びの離散値を用いる必要があります．以下の表に示すように，フーリエ変換にも離散型のものがあります．このうち，離散時間フーリエ変換はコンピュータで取り扱う際に，次の問題があります [資料1]．

• 変換対象の時間信号が無限長となる
• 周波数領域では連続値となる

上記の問題に対して利用されるのが，離散フーリエ変換です．これは，1)時間領域と周波数領域ともに有限の長さで，2)離散値なのでコンピュータで扱いやすいですね．この記事では，Scipyのfftパッケージを用いて，離散フーリエ変換を行うことにします．

	時間領域	周波数領域	Python
離散時間フーリエ変換	離散，非周期(無限長)	連続，周期	Scipy.freqz
離散フーリエ変換	離散，周期	離散，周期	Scipy.fft, numpy.fft.fft

定義

時間領域の離散信号$x[n]$と周波数領域の離散信号$X[k]$は離散フーリエ変換と逆離散フーリエ変換により，次のように結ばれます [資料2]．

\begin{eqnarray}
\begin{cases}
\displaystyle
X[k] = \frac{1}{N} \sum_{n=0}^{N-1} x[n] \exp \left(  -j \frac{2 \pi kn}{N} \right) \\
\displaystyle
x[n] = \sum_{k=0}^{N-1} X[k] \exp \left(   j \frac{2 \pi kn}{N} \right)
\end{cases}
\tag{1}
\end{eqnarray}

ここに，$N$はフーリエ変換・逆フーリエ変換を施す際のサンプル点数です．なお，参考書では**$N$点フーリエ変換**とか言います．

実装上の留意点

Pythonを使って実装する際の留意点をまとめます．

サンプリング周波数と時間配列

サンプリング周波数$f_s=1/T_s$ Hzは，(サンプリング定理から)信号周波数$f_c$の2倍以上を設定するとよいです．このとき，時間領域の信号$x[n]$は，$1/f_s=T_s$秒間隔でサンプリングされることになりますね．

Pythonで時間配列を生成するには，例えば，t=numpy.arange(start=t1,stop=t2,step=1/Ts)とすればよいですね　(t1・t2:開始・終了時刻[s]，step:サンプリング周期[s])．

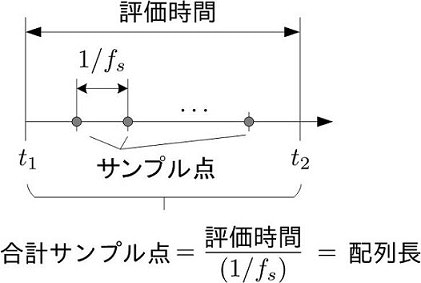
■補足: 評価時間の中に存在するサンプル点数(=時間配列の長さ)は次のようになります．

サンプル点数=\frac{評価時間}{(1/f_s)}=\frac{評価時間}{T_s}

例えば，信号周波数を$f_c=10$ Hz，サンプリング周波数は十分に大きくとった$f_s= 32 \times f_c$とします．このとき，評価時間を2秒とすれば，その中のサンプル点は，評価時間$/(1/f_s)=2 \cdot 32 \cdot 10=640$点となります．

ここまでの実装例(1)

周波数$f_c=10~$Hzの正弦波信号(時刻0～2s)を，サンプリング周波数$f_s=32\cdot f_c$でサンプリングするコードを以下に示します．

import numpy as np

# 信号周波数
fc = 10
# サンプリング周波数
fs = 32 * fc
# 時間ポイント( 長さ=2[s]/(1/fs)=2*32*10=640点 )
t = np.arange(start=0, stop=2, step=1/fs)
# 信号
x = np.cos(2*np.pi*fc*t)

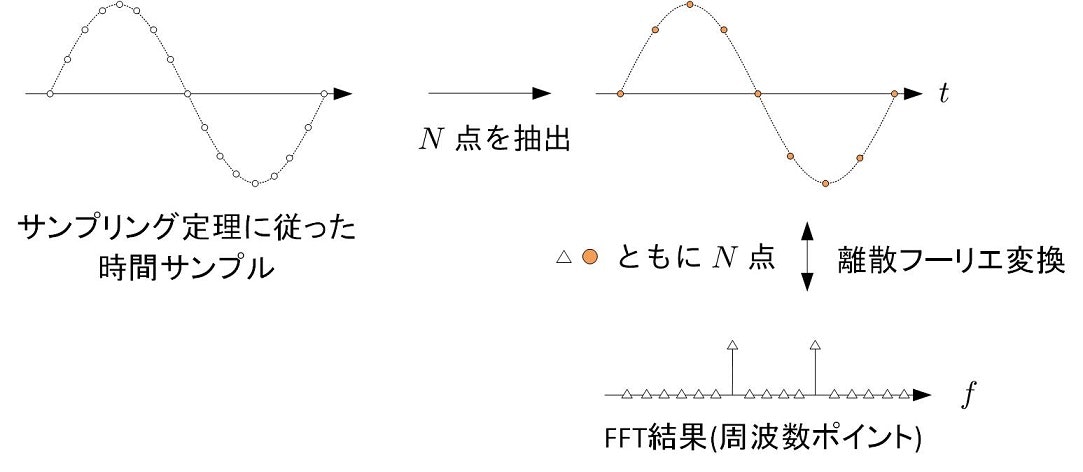
離散フーリエ変換を行うサンプリング点N

前節で，$評価時間/(1/f_s)$[点]でサンプルされた信号を作りましたが，このサンプル点から$N$点を選択してフーリエ変換を施します．$N$は，信号の1周期分が含まれるように設定すればよいです．なお，離散フーリエ変換の結果$X[k]$が配列長に一致します．

例えば，信号周波数$f_c=10$ Hz，サンプリング周波数$f_s= 32 \times f_c$とします．この時，1周期分$1/f_c=1/10=0.1 $秒間に存在するサンプルは，$0.1/f_s=32$点です．したがって，FFTを行うサンプリング点は$N > 32$とすればよいことになります．

周波数と配列のインデックスの関係

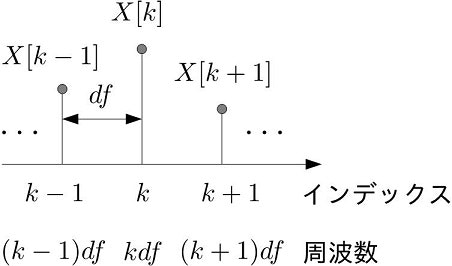
Scipyのfft()結果は配列として返却されますが，配列のインデックスと周波数の関係を述べます．周波数間隔$df$は，サンプリング周波数$f_s$とFFTサンプル点数$N$の比により与えられます．

df = \frac{f_s}{N}
~~\therefore~
k番目 \leftrightarrow k df = k \frac{f_s}{N}

このため，下図に示すような配列インデックスと周波数の関係があることが分かりますね．

ここまでの実装例(2)

# 実装例(1)の途中より追記
from scipy.fftpack import fft

# FFT実行(N点)
X = fft(x, N)
# 周波数軸の生成
# 1[周波数index]あたりの周波数間隔df=fs/N
df = fs/N

# [周波数index]生成
sampleIndex = np.arange(start=0, stop=N)
# [周波数index] --> 周波数間隔を反映
f = sampleIndex*df

離散フーリエ変換の結果（配列の構造）

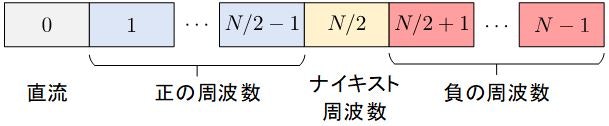
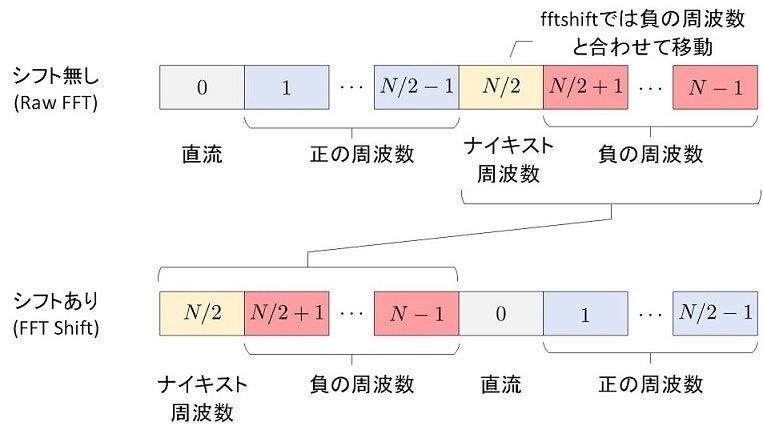
ScipyのFFT結果は，配列として返却されますが，どのような構造になっているのでしょうか．フーリエ変換結果$X[k]$のインデックス$k$は次のようになっています．(なお，以下の表は，$N$が偶数の時のもので，奇数の時は$N/2$を$(N+1)/2$と置き換えてください)．

配列のインデックス$k$	中身
$0$	直流(0 Hz)
$1 ～ (N/2-1)$	正の周波数成分
$N/2$	ナイキスト周波数(=サンプリング周波数/2)
$(N/2+1) ～ (N-1)$	負の周波数成分

ところで，Scipyには，上図に示したFFT結果を並び替えるfftshift()関数が用意されていて，下図のような並び替えを行ってくれます．その際，変換結果の配列の中央に位置するナイキスト周波数(=サンプリング周波数/2)成分は，負の周波数とまとめて移動される点にご注意ください．

ここまでの実装例(3)

ffshiftを考慮したFFTを行うコードを以下に示します．

# 実装例(3)より追記
from scipy.fftpack import fftshift

# FFTシフト検証（ X=fft(x,N) ）
Shifted_X = fftshift(X)
# FFTシフト後の[周波数index]生成(//は整数割り)
Shifted_sampleIndex = np.arange(-N//2, N//2)
# FFTシフト後の[周波数index] --> 周波数間隔dfへ
Shifted_f = Shifted_sampleIndex*df

振幅スペクトル

fftの結果$X[k]$は，一般に複素数となります．この時，振幅スペクトルは実部$X_{re}$と虚部$X_{im}$を用いて次のように与えられます．

|X[k]| = \sqrt{ X_{re}^2 + X_{im}^2 }

振幅スペクトルをプロットする際は例えばnumpy.abs()関数を使います．また，Scipyのfft()結果$X[k]$は，FFTポイント数$N$倍となっているため，X/Nとする必要があります．

まとめ

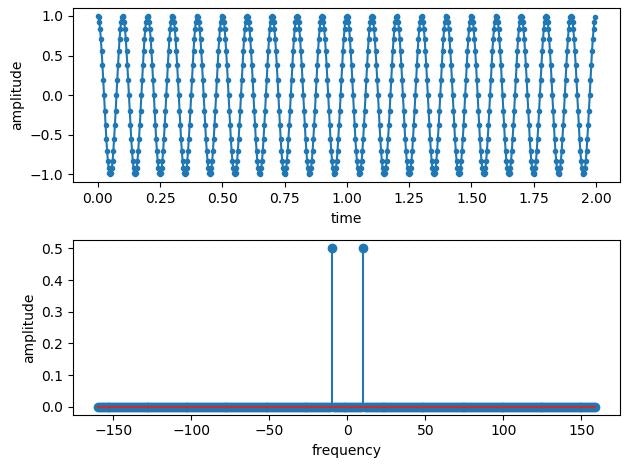
以上の留意点を考慮して，時刻0～2sの正弦波信号（周波数$10$ Hz，サンプリング周波数$f_s=32f_c$）を離散フーリエ変換してみます．以下にソースコードと実行結果を示します．実行結果より，$\pm10$ Hzにスペクトルが立っていますね．これは，$\cos()$のフーリエ変換が

\begin{eqnarray}
\begin{cases}
\displaystyle
x(t)=\cos(2 \pi f_c t)=\frac{1}{2} (\exp(j2\pi f_c t) + \exp(-j2\pi f_c t)  ) \\
\displaystyle
X(f) = \frac{1}{2} ( \delta(f-f_c)+\delta(f+f_c) )
\end{cases}
\end{eqnarray}

となるので，$\pm f_c$ Hzに(信号振幅の1/2の)インパルス$\delta(t)$が立つ(今回は$\pm 10$ Hzに大きさ0.5のスペクトル)ことに対応しています．

import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft, fftshift

# ------------------------------------------------------
# 信号周波数
fc = 10
# サンプリング周波数
fs = 32 * fc
# 時間ポイント( 長さ=2[s]/(1/fs)=2*32*10=640点 )
t = np.arange(start=0, stop=2, step=1/fs)
# 信号
x = np.cos(2*np.pi*fc*t)

# ------------------------------------------------------
# FFTサンプル点数(>1周期の時間ポイント数)
N = 256
# FFT実行(N点)
X = fft(x, N)
# 周波数軸の生成
# 1[周波数index]あたりの周波数間隔df=fs/N
df = fs/N

# ------------------------------------------------------
# FFTシフト
Shifted_X = fftshift(X)
# FFTシフト後の[周波数index]生成(//は整数割り)
Shifted_sampleIndex = np.arange(-N//2, N//2)
# FFTシフト後の[周波数index] --> 周波数間隔dfへ
Shifted_f = Shifted_sampleIndex*df

# ------------------------------------------------------
# プロット(ax[0]:時間波形，ax[1]:周波数波形)
fig, ax = plt.subplots(2)
ax[0].plot(t, x, ".-")
ax[0].set_xlabel("time"), ax[0].set_ylabel("amplitude")
ax[1].stem(Shifted_f, np.abs(Shifted_X)/N, use_line_collection=True)
ax[1].set_xlabel("frequency"), ax[1].set_ylabel("amplitude")
plt.tight_layout()
plt.show()

資料

[資料1] 川又ほか，Python対応 ディジタル信号処理，森北出版，2021年．
[資料2] M. Viswanathan et al., Digital Modulations using Python, Independently published, 2019.