はじめに
統計学を勉強していると必ず出てくる相関関数のイメージについてまとめてみました.
相関係数とは何ぞや
2種類のデータが与えられたとき,これらの間にはどのような関係があるのかを知りたいことがあります.例えば,
- 親の身長と子の身長
- 飲酒年数とがんの発生率
などがありますね.
このような2つのデータ(変量)を$x$と$y$とするとき,**相関係数(correlation coefficient)$r$**を次のように定義します.
$$
\begin{equation}
r=\frac{1}{NS_xS_y}(x_1-\overline{x})(y_1-\overline{y})+(x_2-\overline{x})(y_2-\overline{y})+\cdots+(x_2-\overline{x})(y_2-\overline{y})
\end{equation}
$$
但し,$\overline{x}$と$\overline{y}$は$x,y$の平均,$S_xとS_y$は$xとy$の標準偏差です.
相関係数$r$は常に
-1 \leq r \leq 1
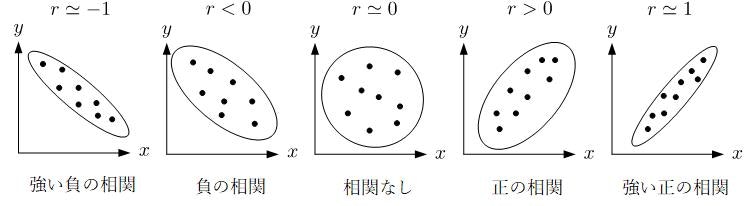
を満たし,下図のような関係となります.
共分散とは何ぞや
共分散は2変量のばらつきを表すものです.
$N$組のデータ$(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)$が与えらえれているとき,共分散(covariance)$S_{xy}$を次のように定義します.
S_{xy}=\frac{1}{N}\Bigl\{
(x_1-\overline{x})(y_1-\overline{y})+(x_2-\overline{x})(y_2-\overline{y})+\cdots+(x_2-\overline{x})(y_2-\overline{y})\Bigr\}
もうお気づきかもしれませんが,相関係数に似ていますよね.この共分散$S_{xy}$を用いると,相関係数の式は次のように書き換えられます.
相関係数r=\frac{S_{xy}}{S_x \cdot S_y}=\frac{xとyの共分散 \ \ \ \ }{\sqrt{xの分散 \ \ \ \ }\sqrt{yの分散 \ \ \ \ }}\ \
ベクトルを用いた説明
"なぜrという数値が2つの変量$x,y$の関係を示している"のでしょうか.統計解析を広い意味で捉えると空間構造を調べていると言え,ここではベクトルを用いて説明してみたいと思います.
2つのベクトル
\begin{equation}
\boldsymbol{x}=(x_1, x_2,\cdots, x_N),\ \ \ \boldsymbol{y}=(y_1, y_2,\cdots, y_N)
\end{equation}
があり,その内積$\boldsymbol{x}\cdot\boldsymbol{y}$は
\begin{align}
\boldsymbol{x}\cdot\boldsymbol{y}&=x_1y_1+x_2y_2+\cdots+x_Ny_N \\
&=||\boldsymbol{x}||\cdot||\boldsymbol{y}||\cos\theta
\end{align}
で定義されています.但し,
\begin{align}
||\boldsymbol{x}||=\sqrt{x_1^2+x_2^2+\cdots+x_N^2} \\
||\boldsymbol{y}||=\sqrt{y_1^2+y_2^2+\cdots+y_N^2}
\end{align}
これを変形していくと,
\begin{align}
\cos\theta&=\frac{\boldsymbol{x}\cdot\boldsymbol{y}}{||\boldsymbol{x}||\cdot||\boldsymbol{y}||} \\
&=\frac{x_1y_1+x_2y_2+\cdots+x_Ny_N}{\sqrt{x_1^2+x_2^2+\cdots+x_N^2}\sqrt{y_1^2+y_2^2+\cdots+y_N^2}} \\
&=\frac{(x_1y_1+x_2y_2+\cdots+x_Ny_N)/N}
{\sqrt{(x_1^2+x_2^2+\cdots+x_N^2)/N}
{\sqrt{(y_1^2+y_2^2+\cdots+y_N^2)}/N}} \\
&=\cfrac{xとyの共分散}{\sqrt{xの分散 \ \ \ \ }\sqrt{yの分散 \ \ \ \ }} \\
\end{align}
つまり,
相関係数=\cos\theta
です.この$\theta$とは2つのベクトル$\boldsymbol{x}と\boldsymbol{y}$のなす角
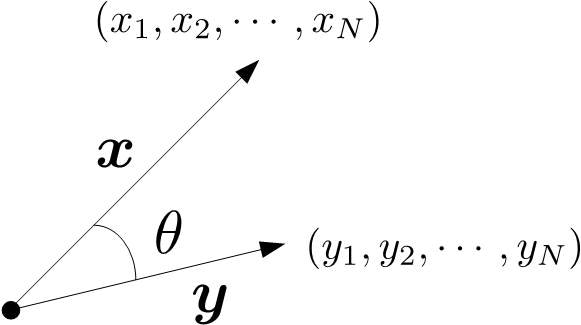
のことです.
したがって,
2つの変量$\boldsymbol{x}と\boldsymbol{y}$の関係 $\leftrightarrow$ 2つのベクトル$\boldsymbol{x}と\boldsymbol{y}$のなす角
$\leftrightarrow$ 2変量$xとy$の相関関数
となり,次の様になります.

例えば,$r \simeq -1$の場合,上の図で示していたように強い負の相関があるとしました.これをベクトルで考えると,2つのベクトル$\boldsymbol{x}$と$\boldsymbol{y}$の向きが**$180^{\circ}$異なっている**ことを意味しています.
同じように,$r \simeq 1$の場合,強い正の相関があると説明しました.これをベクトルで例えると,2つのベクトル$\boldsymbol{x}$と$\boldsymbol{y}$が同じ向きであるということです.
参考
岩村貞夫,"統計解析のはなし",東京図書,1989年