$$
\newcommand{\bm}[1]{\boldsymbol{#1}}
\newcommand{\jiko}[1]{\bm{\dot{#1}}}
\newcommand{\pt}[0]{\partial}
\newcommand{\pcfrac}[2]{\cfrac{\partial #1}{\partial #2}}
\newcommand{\ppcfrac}[2]{\cfrac{\partial^2 #1}{\partial #2^2}}
\newcommand{\ds}[0]{\displaystyle}
$$
はじめに
前回まとめた記事「動的電磁界の求め方」では,電磁波が時間変動するときの電磁界の求め方を紹介しました.例えば,磁界は直接求めるのではなく,遅延ベクトルポテンシャルを介して計算します.この記事では,これを応用して,遅延ベクトルポテンシャルを使って,微小電流源によるアンテナが放射する電磁界を求めてみます.本記事の最後に,Pythonを使った簡単なアンテナ放射特性(指向性)を計算するプログラムも示します.
アイディア
前述のように,磁界$\jiko{B}$は観測地点に作り出された遅延ベクトルポテンシャル$\jiko{A}$を介して求められます.
$$
\jiko{B} = \nabla \times \jiko{A} \tag{1}
$$
この記事では,電磁波として周期的に変動する複素正弦波を仮定します.その意味で,式(1)の電界$\jiko{B}$と遅延ベクトルポテンシャル$\jiko{A}$にドット記号を付けています.なお,複素正弦波振動する電磁界については以下の記事にまとめています.
ここで,式(1)の遅延ベクトルポテンシャル$\jiko{A}$の各成分$(\dot{A}_x,\dot{A}_y,\dot{A}_Z)$は次のように与えられます.
\begin{eqnarray}
\begin{cases}
\dot{A}_x(\bm{r})
= \cfrac{\mu}{4\pi}
\ds\int \cfrac{
|\dot{I}_x(\bm{r})|
e^{-jk|\bm{r}-\bm{r'}|}
}{
|\bm{r} - \bm{r}' |
} \bm{dr'}
\\
\dot{A}_y(\bm{r})
= \cfrac{\mu}{4\pi}
\ds\int \cfrac{
|\dot{I}_y(\bm{r})|
e^{-jk|\bm{r}-\bm{r'}|}
}{
|\bm{r} - \bm{r}' |
} \bm{dr'}
\\
\dot{A}_z(\bm{r})
= \cfrac{\mu}{4\pi}
\ds\int \cfrac{
|\dot{I}_z(\bm{r})|
e^{-jk|\bm{r}-\bm{r'}|}
}{
|\bm{r} - \bm{r}' |
} \bm{dr'}
\end{cases}
\tag{2}
\end{eqnarray}
式(1)で未知の成分は**電流分布$(\dot{I}_x,\dot{I}_y,\dot{I}_z)$**ですね.これが分かれば,図1のような流れでアンテナから放射される電磁界が分かります.
微小電流源が作る電磁界
記事「動的電磁界の求め方」で述べたように,電流が電磁波の放射源(波源)となります.そこで,この記事では微小な電流源をアンテナとし,そこから放射される電磁界を解析します.
条件設定
次のような条件の微小電流源を考えます.
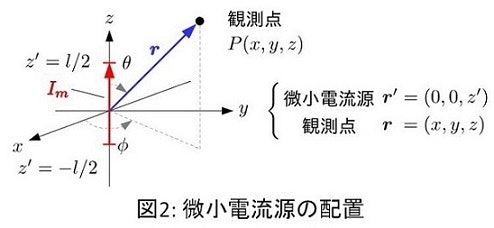
■ 条件1 図2のように電流源を$z$軸上に配置する.この時,電流源の長さは$l~(-l/2<z<l/2)$とする.
■ 条件2 電流源の位置ベクトルを$\bm{r'}=(0,0,z')$とする.ただし,電流源の長さ$|\bm{r'}|=l$は,観測地点の位置ベクトル$\bm{r}=(x,y,z)$の大きさ$|\bm{r}|$に対して十分小さい(観測地点が十分に離れている$|\bm{r}| \gg |\bm{r}'|$)とする.
■ 条件3 (条件2)より電流源は長さが微小なので,電流は微小電流源の至る所で一定とする.
これらの条件に対して,以降,図1の流れに沿って電磁界を解析してみます.
Step1) 電流分布
(条件2)と(条件3)より,一定の電流値を$I_m$と置くと,電流分布は次のようになりますね.
\begin{eqnarray}
\begin{cases}
|\dot{I}_x (\bm{r}')|=0 \\
|\dot{I}_y (\bm{r}')|=0 \\
|\dot{I}_z (\bm{r}')|=I_m
\end{cases}
\tag{3}
\end{eqnarray}
Step2) 遅延ベクトルポテンシャル
式(3)の電流分布を前述の遅延ベクトルポテンシャルの式(2)に放り込みます.
\begin{eqnarray}
\begin{cases}
\dot{A}_x(\bm{r})
&= \cfrac{\mu}{4\pi}
\ds\int \cfrac{
|\dot{I}_x(\bm{r})|
e^{-jk|\bm{r}-\bm{r'}|}
}{
|\bm{r} - \bm{r}' |
} \bm{dr'}
= 0 \\
%------
\dot{A}_y(\bm{r})
&= \cfrac{\mu}{4\pi}
\ds\int \cfrac{
|\dot{I}_y(\bm{r})|
e^{-jk|\bm{r}-\bm{r'}|}
}{
|\bm{r} - \bm{r}' |
} \bm{dr'}
= 0
\\
%------
\dot{A}_z(\bm{r})
&= \cfrac{\mu}{4\pi}
\ds\int \cfrac{
|\dot{I}_z(\bm{r})|
e^{-jk|\bm{r}-\bm{r'}|}
}{
|\bm{r} - \bm{r}' |
} \bm{dr'}
= \cfrac{\mu}{4\pi}
\ds\int^{l/2}_{-l/2} \cfrac{
I_m
e^{-jk \sqrt{x^2 + y^2 + (z-z')^2} }
}{
\sqrt{x^2 + y^2 + (z-z')^2}
} dz
\end{cases}
\tag{4}
\end{eqnarray}
上の第3式について,微小電流源の位置ベクトルは$\bm{r'}=(0,0,z')$であり,観測地点の位置ベクトルは$\bm{r}=(x,y,z)$です.このとき,$|\bm{r-r'}|=\sqrt{(x-0)^2+(y-0)^2+(z-z')^2}$です.ここで,(条件2)より,観測地点が十分に離れている($|\bm{r}|\gg|\bm{r'}|$)ことを考慮すると,$z \gg z'$ですので,式(4)の$|\bm{r-r'}|$は次の近似ように近似できます.
$$
|\bm{r-r'}|=\sqrt{(x-0)^2+(y-0)^2+(z-z')^2} \simeq \sqrt{x^2+y^2+z^2}
$$
これを考慮して式(4)を積分すれば,遅延ベクトルポテンシャルは次のようになります.
\begin{eqnarray}
\begin{cases}
\dot{A}_x(\bm{r})
&= \dot{A}_x(x,y,z)
= 0 \\
%------
\dot{A}_y(\bm{r})
&= \dot{A}_y(x,y,z)
= 0 \\
%------
\dot{A}_z(\bm{r})
&= \dot{A}_x(x,y,z)
= \cfrac{\mu l I_m}{ 4 \pi r } e^{-jkr}
\end{cases}
\tag{5}
\end{eqnarray}
ところで,アンテナから出た電磁波は,放射状に広がっていくので極座標を用いた方が直感的ですね.そこで,求めた遅延ベクトルポテンシャル$\dot{A}(\bm{r})$を極座標に変換しておきましょう.一般に,直交座標から極座標への変換
(\dot{A}_x,\dot{A}_y,\dot{A}_z)
\quad\rightarrow\quad
(\dot{A}_r, \dot{A}_\theta, \dot{A}_{\phi})
は次のように与えられます.
\begin{eqnarray}
\begin{cases}
\dot{A}_r
= \dot{A}_x \sin{\theta} \cos{\phi}
+ \dot{A}_y \sin{\theta} \sin{\phi}
+ \dot{A}_z \cos{\theta} \\
\dot{A}_\theta
= \dot{A}_x \cos{\theta} \cos{\phi}
+ \dot{A}_y \cos{\theta} \sin{\phi}
+ \dot{A}_z \sin{\theta} \\
\dot{A}_\phi
= - \dot{A}_x \sin{\phi}
+ \dot{A}_y \cos{\phi}
\end{cases}
\end{eqnarray}
この関係を用いれば,式(5)の遅延ベクトルポテンシャルの極座標が以下のように表現できます.
\begin{eqnarray}
\begin{cases}
\dot{A}_r
&= \cfrac{\mu l I_m}{ 4 \pi r } e^{-jkr} \cos{\theta} \notag\\
\dot{A}_\theta
&= - \cfrac{\mu l I_m}{ 4 \pi r } e^{-jkr} \sin{\theta} \\
\dot{A}_\phi
&= 0
\end{cases}
\tag{6}
\end{eqnarray}
Step3) 磁界の計算
では,いよいよ磁界$\jiko{B}$を計算します.式(1)で示したように磁界$\jiko{B}$は遅延ベクトルポテンシャル$\jiko{A}$の回転で計算できます.
$$
\jiko{B} = \nabla \times \jiko{A} \tag{再掲1}
$$
今考えている座標は極座標です.一般に,極座標の回転$\nabla \times \dot{A}$は次のように与えられます.
\begin{align}
\nabla \times \jiko{A}
&=(
(\nabla \times \jiko{A})_{r},~
(\nabla \times \jiko{A})_\theta,~
(\nabla \times \jiko{A})_\phi
) \\
%
&= \left(
\cfrac{1}{r\sin{\theta}} \left[
\pcfrac{}{\theta} A_\phi \sin{\theta}
- \pcfrac{A_\theta}{\phi}
\right],
%
\cfrac{1}{r} \left[
\cfrac{1}{ \sin{\theta} } \pcfrac{A_r}{\phi}
- \pcfrac{}{r} r A_\phi
\right],
%
\cfrac{1}{r} \left[
\pcfrac{}{r} r A_\theta
- \pcfrac{A_r}{r}
\right]
\right)
\end{align}
これを用いて,式(6)の回転を求めると,次のように磁界$\jiko{B}$が求まります.
$$
\jiko{B}
= \nabla \times \jiko{A}
= \left(
0,~
0,~
jk \cfrac{\mu l I_m \sin{\theta}}{ 4 \pi r} e^{-jkr}
+ \cfrac{\mu l I_m \sin{\theta}}{ 4 \pi r^2} e^{-jkr}
\right)
\tag{7}
$$
Step4) 電界の計算
最後に電界$\jiko{E}$を求めましょう.今,磁界$\jiko{B}$は式(7)で既に求めています.そこで,拡張されたアンペールの法則を変形して,
$$
\nabla \times \jiko{H}
= (\sigma+j \omega \epsilon) \jiko{E}
\quad\rightarrow\quad
\jiko{E}
= \cfrac{ \nabla \times \jiko{H} }{ \sigma+j \omega \epsilon }
$$
から電界$\jiko{E}$を求めることにしましょう.ただし,ここでは$\sigma=0$の無損失媒質を仮定して,$\jiko{B}=\mu\jiko{H}$を用いて次のように変形しておきます.
$$
\jiko{E}
= \cfrac{1}{j \omega \epsilon \mu} \left(
\nabla \times \jiko{B}
\right) \tag{8}
$$
まず,式(8)右辺の磁界$\jiko{B}$の回転
\nabla \times \jiko{B}
=(
(\nabla \times \jiko{B})_{r},
(\nabla \times \jiko{B})_\theta,~
(\nabla \times \jiko{B})_\phi
)
の各成分を求めましょう.前述の極座標に対する回転公式から$\nabla \times \jiko{B}$の各成分が次のように与えられます.
\begin{eqnarray}
\begin{cases}
(\nabla \times \jiko{B})_{r}
= jk \cfrac{ \mu l I_m \cos{\theta} }{2 \pi r^2} e^{-jkr}
+ \cfrac{ \mu l I_m \cos{\theta} }{2 \pi r^3} e^{-jkr} \\
(\nabla \times \jiko{B})_\theta
= k^2 \cfrac{ \mu l I_m \sin{\theta} }{ 4 \pi r } e^{-jkr}
+ (jkr+1) \cfrac{ \mu l I_m \sin{\theta} }{ 4 \pi r^3 } e^{-jkr} \\
(\nabla \times \jiko{B})_\phi
= 0
\end{cases}
\end{eqnarray}
したがって,これを式(8)に放り込むことで,電界$\jiko{E}$が定まります.
\begin{eqnarray}
\begin{cases}
\dot{E}_r
&= -j \cfrac{1}{\omega \mu \epsilon} \left(
jk \cfrac{ \mu l I_m \cos{\theta} }{2 \pi r^2} e^{-jkr}
+ \cfrac{ \mu l I_m \cos{\theta} }{2 \pi r^3} e^{-jkr}
\right) \notag\\
%
&= \cfrac{ klI_m \cos{\theta} }{ 2 \pi \omega \epsilon r^2 } e^{jkr}
- j \cfrac{ lI_m \cos{\theta} }{ 2 \pi \omega \epsilon r^3 } e^{jkr}\\
%------
\dot{E}_\theta
&= -j \cfrac{1}{\omega \mu \epsilon} \left(
k^2 \cfrac{ \mu l I_m \sin{\theta} }{ 4 \pi r } e^{-jkr}
+ (jkr+1) \cfrac{ \mu l I_m \sin{\theta} }{ 4 \pi r^3 } e^{-jkr}
\right) \\
%
&= j \cfrac{ k^2 l I_m \sin{\theta} }{ 4 \pi \omega \epsilon r} e^{-jkr}
+ \cfrac{ k l I_m \sin{\theta} }{ 4 \pi \omega \epsilon r^2} e^{-jkr}
- j \cfrac{ l I_m \sin{\theta} }{ 4 \pi \omega \epsilon r^3} e^{-jkr}
\notag\\
%------
\dot{E}_\phi
&= 0
\notag
\end{cases}
\tag{9}
\end{eqnarray}
考察
改めて,求めた電磁界を書き並べると次のようになります.
\begin{eqnarray}
\begin{cases}
\dot{B}_r
= 0 \\
\dot{B}_\theta
=0 \\
\dot{B}_\phi
=jk \cfrac{\mu l I_m \sin{\theta}}{ 4 \pi r} e^{-jkr}
+ \cfrac{\mu l I_m \sin{\theta}}{ 4 \pi r^2} e^{-jkr}
\end{cases}
\tag{再掲7}
\end{eqnarray}
\begin{eqnarray}
\begin{cases}
\dot{E}_r
&= \cfrac{ klI_m \cos{\theta} }{ 2 \pi \omega \epsilon r^2 } e^{jkr}
- j \cfrac{ lI_m \cos{\theta} }{ 2 \pi \omega \epsilon r^3} e^{jkr}\\
%------
\dot{E}_\theta
&= j \cfrac{ k^2 l I_m \sin{\theta} }{ 4 \pi \omega \epsilon r} e^{-jkr}
+ \cfrac{ k l I_m \sin{\theta} }{ 4 \pi \omega \epsilon r^2} e^{-jkr}
- j \cfrac{ l I_m \sin{\theta} }{ 4 \pi \omega \epsilon r^3} e^{-jkr}
\notag\\
%------
\dot{E}_\phi
&= 0
\notag
\end{cases}
\tag{再掲9}
\end{eqnarray}
電磁波の減衰?
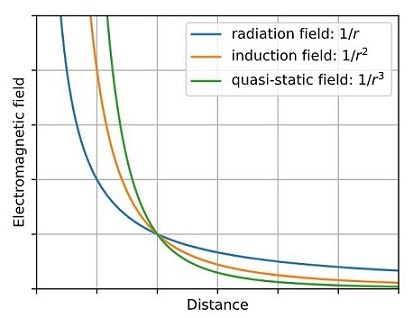
式(7)と(9)の各項はごちゃごちゃしていますね.実は,各項をあえて距離$r$について$1/r$,$1/r^2$,$1/r^3$の3つに分けて記述しました.$r$は微小電流源からの距離を表していますから,各項は距離が離れるにつれて電磁界が減衰する様子を表しています.アンテナから十分に離れた地点では$1/r$の項が効いてきます.この項は実質的に電磁波の放射に寄与するので放射界(radiation field)と呼びます.また,$1/r^2$の項を誘導界(induction-field),$1/r^3$の項を**準静電界(quasi-static field)**と呼びます.
アンテナの放射方向?
アンテナから十分離れた地点では放射界($1/r$項)が支配的です.例えば,遠方における電界$\jiko{E}$なら,誘導界($1/r^2$)と準静電界($1/r^3$)を無視できるので,式(9)は次のように近似できますね.
\jiko{E}
= \left(
\dot{E}_r,
\dot{E}_\theta,
\dot{E}_\phi
\right)
= \left(
0,
0,
j \cfrac{ k^2 l I_m \sin{\theta} }{ 4 \pi \omega \epsilon r} e^{-jkr}
\right)
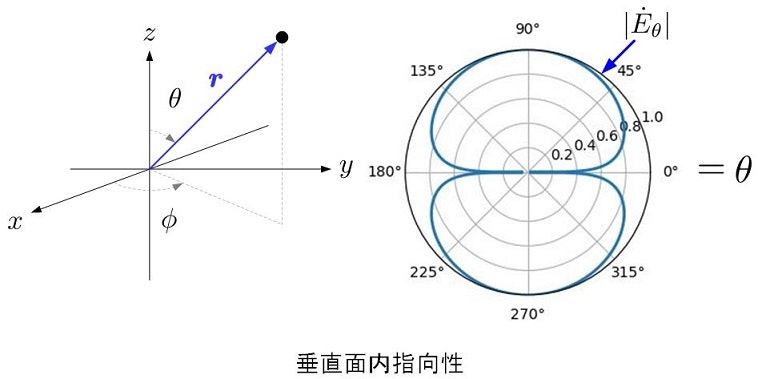
この式から,$z$軸を含む平面で考えると,$\theta=90^\circ, 270^\circ$方向で電界が最大となります.この様子をプロットしてみます.上の式より電界$\jiko{E}$の大きさは
$$
|\jiko{E}|
=|\dot{E}_\theta|
=\left|
\cfrac{ k^2 l I_m \sin{\theta} }{ 4 \pi \omega \epsilon r}
\right|~~(\because~|j|=1,~|e^{-jkr}|=1)
\tag{10}
$$
となるので,$r=$一定とすると,下図のような特性が得られます(最大値で規格化し,logスケールで表示).
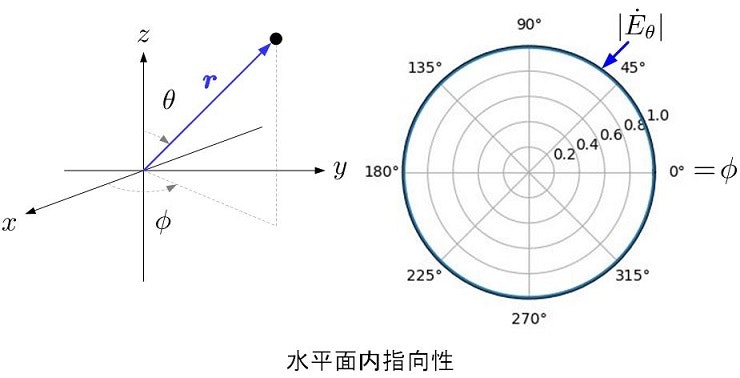
このように,度の向きに強く放射できるかを示す特性を指向特性とか指向性とよびます.微小電流源のアンテナの場合は,$90^\circ, 270^\circ$方向に強く電波を放射できると言いかえることができますね.この$z$軸を含む平面上の放射特性を垂直面内指向特性と言います.垂直があるということは水平もあります.式(10)を眺めると$\phi$には依存しませんね.これは$x-y$平面を含む面上では距離が一定のとき,電界の大きさが一定となります.この様子を下図に示します.この$x-y$平面を含む平面上での指向特性を水平面内指向特性とか言います.
指向性を描画するPythonプログラム
以下,念のために指向特性を描くpythonプログラムを掲示します.
import numpy as np
import matplotlib.pyplot as plt
f = 1 * (10**9) # 1 GHz
lamb = 3*(10**8)/f # 波長
k = 2*np.pi/lamb # 波数
omega = 2*np.pi*f # 角周波数
epsilon = 8.8541*10**(-12) # 誘電率
I_m = 1 # 電流
l = 1 # 電流源の長さ
r = 1 # 微小電流源からの距離
N = 1000
# 垂直面内指向性
theta = np.linspace(0, 2*np.pi, N)
E_theta = np.abs(
k * k * l * I_m * np.sin(theta) / (4*np.pi*omega*epsilon*r)
)
# 水平面内指向性(θ=90で固定)
theta_fixed = np.linspace(np.pi/2, np.pi/2, N)
E_phi = np.abs(
k * k * l * I_m * np.sin(theta_fixed) / (4*np.pi*omega*epsilon*r)
)
# logスケール化(if文はlog 0回避)
for i in range(N):
if(E_theta[i] != 0):
E_theta[i] = 10*np.log10(E_theta[i])
if(E_phi[i] != 0):
E_phi[i] = 10*np.log10(E_phi[i])
# 規格化(最大値1)
E_theta = E_theta/max(E_theta)
E_phi = E_phi/max(E_phi)
# プロット
fig = plt.figure()
# 垂直面内指向性
ax = fig.add_subplot(121, projection="polar")
ax.plot(theta, E_theta, linewidth=2.0)
ax.set_ylim(0, max(E_theta))
ax.set_title("vertical-directivity", pad=20)
# 水平面内指向性
ax = fig.add_subplot(122, projection="polar")
ax.plot(theta, E_phi, linewidth=4.0)
ax.set_ylim(0, max(E_phi))
ax.set_title("horizontal-directivity", pad=20)
# 出力
plt.tight_layout()
plt.show()