LoginSignup
1
2

More than 1 year has passed since last update.

@epppJones

第8回　動的電磁界の求め方

Last updated at Posted at 2021-08-27

$$
\newcommand{\bm}[1]{\boldsymbol{#1}}
\newcommand{\jiko}[1]{\bm{\dot{#1}}}
\newcommand{\pt}[0]{\partial}
\newcommand{\pcfrac}[2]{\cfrac{\partial #1}{\partial #2}}
\newcommand{\ppcfrac}[2]{\cfrac{\partial^2 #1}{\partial #2^2}}
\newcommand{\ds}[0]{\displaystyle}
$$

はじめに

これまで，時間変動のない静的な電磁界の求め方としてスカラーポテンシャルやベクトルポテンシャルを介した方法を紹介させていただきました．電磁界が動的に変動する場合にも，スカラーポテンシャルやベクトルポテンシャルを介して電磁界が求められます．

伝導電流が波源となる？

結論から言うと，伝導電流$\bm{j}$は波源となります．その直感的な理由を説明します．

1) 拡張されたアンペールの法則より伝導電流$\bm{j}$の周囲に磁界$\bm{H}$ができます．

$$
\nabla \times \bm{H}
= \bm{j} + \pcfrac{\bm{D}}{t}
$$

2) この磁界$\bm{B}$は時間変動するので，ファラデーの電磁誘導の法則から，その周囲に電界$\bm{E}$が生じます．

$$
\nabla \times \bm{E} = - \pcfrac{\bm{B}}{t}
$$

3) 生じた電界$\bm{E}$もまた時間変動するので，拡張されたアンペールの法則より，再び磁界を生じさせる.

$$
\nabla \times \bm{H}
= \bm{j} + \pcfrac{\bm{D}}{t}
$$

以上の繰り返しにより電磁波が生じさせます．つまり，伝導電流$\bm{j}$が波源となります．このような理由から，本記事では伝導電流が作る電磁波を考えます．

マクスウェル方程式とポテンシャル（電磁ポテンシャル方程式）

電磁界が動的に変動する場合のマクスウェル方程式は次のように与えられます．

\begin{eqnarray}
\begin{cases}
\nabla \cdot \boldsymbol{D}& = \rho
    &(電束密度に関するガウスの法則) \\
\nabla \cdot \boldsymbol{B} &= 0
    &(磁束密度に関するガウスの法則) \\
\nabla \times \boldsymbol{H}
    &= \boldsymbol{j} 
    + \cfrac{\partial \boldsymbol{{D}}}{\partial t}
    &(拡張されたアンペールの法則)   \\
\nabla \times \boldsymbol{E}
    &= - \cfrac{\partial \boldsymbol{{B}}}{\partial t}
    &(ファラデーの電磁誘導の法則)  
\end{cases}
\end{eqnarray}

くどいようですが，マクスウェル方程式を直接連立して電磁界を解くのは骨が折れるので，電磁界が作るポテンシャルを介して電磁界を求めるという手順を踏みます．このため，以降では電磁界の方程式をポテンシャルの方程式に変換します．

動的磁界の関するポテンシャルの方程式

まず，磁界$\bm{H}$は，直流磁界を求めたときと同様に次のように与えられます．

$$
\bm{B} = \nabla \times \bm{A} \tag{1}
$$

ここで，$\bm{A}$が磁界$\bm{B}$が生み出すベクトルポテンシャルです．

動的電界に関するポテンシャルの方程式

電界$\bm{E}$についてもポテンシャルを用いて表現します．まず，式(1)をファラデーの電磁誘導の法則に代入します．

\begin{gather}
\nabla \times \bm{E} 
  = - \cfrac{\pt \bm{{B}}}{\pt t}
  = - \cfrac{\pt }{\pt t} ( \nabla \times \bm{A} )
  = - \nabla \times \cfrac{\pt \bm{A} }{\pt t} \\
\therefore~
\nabla \times \left( \bm{E} + \cfrac{\pt \bm{A} }{\pt t} \right)=\bm{0} \tag{2}
\end{gather}

ここで，ベクトル解析によると，次の関係が常に成立します．

$$
\nabla \times (- \nabla V) = \bm{0} \tag{3}
$$

$V$は電界のスカラーポテンシャルです．式(2)と(3)を見比べると，次の関係が成立しますね．

$$
\nabla \times (- \nabla V)
= \bm{E} + \cfrac{\pt \bm{A} }{\pt t}
\quad\therefore~
\bm{E} = - \cfrac{\pt \bm{A} }{\pt t} - \nabla V \tag{4}
$$

ここまでの整理

改めて，ポテンシャルを用いた電磁界の方程式をまとめると次のようになります．

\begin{eqnarray}
\begin{cases}
\bm{B} = \nabla \times \bm{A} &(再掲1)\\
\bm{E} = - \cfrac{\pt \bm{A} }{\pt t} - \nabla V &(再掲4) 
\end{cases}
\end{eqnarray}

以降では，伝導電流$\bm{j}$が作る電磁界を求めるため，スカラーポテンシャル$V$とベクトルポテンシャル$\bm{A}$を求めます．

ベクトルポテンシャルの求め方

前述のスカラーポテンシャル$V$の方程式(1)とベクトルポテンシャル$\bm{A}$の方程式(4)を$\bm{B}=\mu \bm{H}$および$\bm{D}=\epsilon \bm{E}$の関係を使って変形しておきます．

\begin{eqnarray}
\begin{cases}
\bm{H} = \cfrac{1}{\mu} (\nabla \times \bm{A}) &(変形1)\\
\bm{E} = - \epsilon \pcfrac{\bm{A}}{t} - \epsilon \nabla V &(変形4) 
\end{cases}
\end{eqnarray}

これらの関係を拡張されたアンペールの法則

$$
\nabla \times \bm{H} = \bm{j} + \pcfrac{\bm{D}}{t}
$$

に放り込むと，次のようになります．

\begin{gather}
\nabla \times \left[ \cfrac{1}{\mu} (\nabla \times \bm{A}) \right]
  = \bm{j} + \pcfrac{\bm{D}}{t} \left[ 
      - \epsilon \pcfrac{\bm{A}}{t} - \epsilon \nabla V
  \right] \\
\therefore~~
\nabla \times \nabla \times \bm{A}
  = \mu \bm{j} - \epsilon\mu \ppcfrac{\bm{A}}{t} 
  - \nabla \left( \epsilon\mu \pcfrac{V}{t} \right)
\end{gather}

ここで，ベクトル公式$\nabla \times \nabla \times \bm{A} = \nabla(\nabla \cdot \bm{A})-\nabla^2 \bm{A}$を左辺に適用します．

$$
\nabla(\nabla \cdot \bm{A})-\nabla^2 \bm{A}
= \mu \bm{j} - \epsilon\mu \ppcfrac{\bm{A}}{t}
- \nabla \left( \epsilon\mu \pcfrac{V}{t} \right) \tag{5}
$$

この方程式を解きます．ところで，ヘルムホルツの定理によると，任意のベクトル場$\bm{A}$は，その回転$(\nabla \times \bm{A})$と発散$(\nabla \cdot \bm{A})$により一意に定まります．今，$\bm{A}$の回転はの式(1)に示した通り$\nabla \times \bm{A}=\bm{B}$となります（むしろ，$\nabla \cdot \bm{A}$を定めるべく式(1)を連立させた感じですね）．一方，$\bm{A}$の発散は定まっていません．そのため，このままでは式(5)を満たすベクトルポテンシャル$\bm{A}$は定まりません．これを解決する条件がローレンツ条件です．

ローレンツ条件の登場

式(5)の両辺を見比べて，$\bm{A}$の発散$(\nabla \cdot \bm{A})$を定めるべく，次のような条件を設定しましょう．

$$
\nabla \cdot \bm{A} = -\epsilon\mu \pcfrac{V}{t} \tag{6}
$$

これをローレンツ条件と呼びます（ローレンツ条件のもとで得られたベクトルポテンシャル$\bm{A}$をローレンツゲージでのポテンシャルとか言います）．ローレンツ条件を考慮すると式(5)は次のように表されます．

$$
-\nabla^2 \bm{A}
= \mu \bm{j} - \epsilon\mu \ppcfrac{\bm{A}}{t} \quad\rightarrow\quad
\nabla^2 \bm{A} - \cfrac{1}{c^2} \ppcfrac{\bm{A}}{t} = - \mu \bm{j}~~
\left(\because~v=\cfrac{1}{\sqrt{\epsilon\mu}} \right)
\tag{7}
$$

この方程式は，電流源$\bm{j}$がその周りに作るベクトルポテンシャル$\bm{A}$の様子を表しています．

ところで，この方程式，第1回記事でも述べました電磁界の波動方程式によく似ています．

\begin{eqnarray}
\begin{cases}
\nabla^2 \bm{E} - \cfrac{1}{v^2} \ppcfrac{\bm{E}}{t} = 0 \\
\nabla^2 \bm{H} - \cfrac{1}{v^2} \ppcfrac{\bm{H}}{t} = 0 
\end{cases}
\end{eqnarray}

実は式(7)は電磁界の波動方程式に対応するポテンシャルの方程式となります．第1回では，波源（電流源）がない状況を考えましたが，本記事では波源（電流源）がある状況を想定していますので，式(7)の右辺は0ではありません（非同次微分方程式ですね）．

ベクトルポテンシャルの方程式の解

式(7)のベクトルポテンシャル$\bm{A}$および電流源$\bm{j}$の各成分を

\begin{eqnarray}
\begin{cases}
\bm{A}=(A_x,A_y,A_z) \\
\bm{j}=(j_x,j_y,j_z)
\end{cases}
\end{eqnarray}

と置いて，成分表示すると次のようになります．

\begin{eqnarray}
\begin{cases}
\nabla^2 A_x - \cfrac{1}{v^2} \ppcfrac{A_x}{t} = -\mu j_x　\\
\nabla^2 A_y - \cfrac{1}{v^2} \ppcfrac{A_y}{t} = -\mu j_y　\tag{8}\\
\nabla^2 A_z - \cfrac{1}{v^2} \ppcfrac{A_z}{t} = -\mu j_z　
\end{cases}
\end{eqnarray}

この方程式は，非同次の微分方程式で，直接解くのは容易ではありません．そこで登場するのがグリーン関数です．

グリーン関数の登場

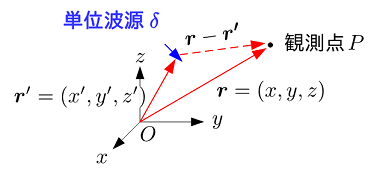
アイディアとしては，いきなり電流源を配置して，それが作るベクトルポテンシャル$\bm{A}$を求めるのではなく，次のような方法をとります．まず，図のように単位波源$\delta$を配置し，それが作るポテンシャル$G$を求めます．最後に，求めたポテンシャル$G$をうまく重ね合わせることで，式(7)の解を求めます．ここでは，式(8)最上段の$x$成分に関する方程式を解きます．

             

単位波源が作るベクトルポテンシャルの方程式

式(7)の右辺は波源を表しているので，これを単位波源に置き替えます．また，それが作るポテンシャルを$G$と置きます．このとき式(7)に対応する方程式が次のようになります．

$$
\nabla^2 G - \cfrac{1}{v^2} \ppcfrac{G}{t} = -\delta(t-t',\bm{r-r'}) \tag{9}
$$

ここで，$G$をグリーン関数で，$\bm{r'}$は単位波源の位置ベクトル，$\bm{r}$は観測地点の位置ベクトルを表しています．$t'$は単位波源での時刻，$t$は観測地点$P$での時刻を表しています．

グリーン関数による解表現

式(9)の解$G$に電流の大きさ駆けて重ね合わせることで，式(8)の解が求められます．

$$
\bm{A}(\bm{r},t)=\iint G(\bm{r}-\bm{r'},t-t')\mu i_x(\bm{r'},t') \bm{dr'} dt' \tag{10}
$$

解法は省略しますが，式(9)の解$G$は次のようになります．

$$
G(\bm{r}-\bm{r'},t-t')
= \cfrac{1}{4 \pi |\bm{r-r'}|}
\delta \left(t-t' - \cfrac{|\bm{r-r'}|}{v} \right)
$$

これを式(10)に放り込むと，ベクトルポテンシャル$A_x$が得られます．

\begin{align}
A_x(\bm{r},t) 
  &= \iint \left[ 
    \cfrac{1}{4 \pi |\bm{r-r'}|} 
    \delta \left(t-t' - \cfrac{|\bm{r-r'}|}{v} \right)  
  \right] i_x(\bm{r'},t') \bm{dr'} dt' \\
  &= \cfrac{\mu}{4\pi} \int \cfrac{1}{4 \pi |\bm{r-r'}|}
       \left[
          \int^{\infty}_{-\infty} 
              i_x(\bm{r'},t') \delta
              \left(t-t' - \cfrac{|\bm{r-r'}|}{v} \right) dt' 
       \right] \bm{dr}' \\
\therefore~
A_x(\bm{r},t)
  &= \cfrac{\mu}{4\pi} \int 
        \cfrac{ 
            i_x \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| }  \tag{11}
\end{align}

再下段の変形ではデルタ関数の性質

$$
x(t) = \int^{\infty}_{-\infty} x(\tau) \delta(t-\tau) d\tau
$$

を使っています．式(11)を眺めると，$i_x$の時刻が$t-(|\bm{r-r'}|/v)$であることが分かりますね．これは，電流源と観測点が$|\bm{r-r'}|$だけ離れているため，電流$i_x$が流れてから観測地点にベクトルポテンシャル$A_x$ができるまでに$t-(|\bm{r-r'}|/v)$なる遅延時間が生じることを意味しています．その意味で，式(11)を遅延ベクトルポテンシャルと呼んでいます．なお，ベクトルポテンシャルの残りの各成分も同様の手順で計算できます．

\begin{eqnarray}
\begin{cases}
A_x(\bm{r},t)
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            i_x \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| }  \bm{dr'}\\
A_y(\bm{r},t)
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            i_y \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| }  \bm{dr'}\\
A_z(\bm{r},t)
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            i_z \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| } \bm{dr'}
\end{cases}
\tag{12}
\end{eqnarray}

スカラーポテンシャルの求め方

最後に，スカラーポテンシャル$V$を導出しましょう．電界$\bm{E}$とそのスカラーポテンシャル$V$の関係を再掲します．

$$
\bm{E} = - \cfrac{\pt \bm{A} }{\pt t} - \nabla V (再掲4)
$$

この両辺の発散をとると

$$
\nabla \cdot \bm{E} = \nabla \cdot \left( - \cfrac{\pt \bm{A} }{\pt t} - \nabla V \right) \tag{13}
$$

ここで，式(13)とガウスの法則

$$
\nabla \cdot \bm{E} = \cfrac{\rho}{\epsilon}
$$

を見比べると次の関係がありますね．

$$
\nabla \cdot \left( - \cfrac{\pt \bm{A} }{\pt t} - \nabla V \right)
= \cfrac{\rho}{\epsilon}
\quad\rightarrow\quad
-\pcfrac{}{t} (\nabla \cdot \bm{A}) - \nabla^2 V = \cfrac{\rho}{\epsilon} \tag{14}
$$

ここで，ローレンツ条件

$$
\nabla \cdot \bm{A} = -\epsilon\mu \pcfrac{V}{t} \tag{再掲6}
$$

を考慮すれば式(13)は次のようになります．

$$
-\pcfrac{}{t} \left( - \epsilon\mu\cfrac{\pt V }{\pt t} \right) - \nabla^2 V = \cfrac{\rho}{\epsilon}
\quad\rightarrow\quad
\nabla^2 V - \cfrac{1}{v^2} \ppcfrac{V}{t} = - \cfrac{\rho}{\epsilon}
$$

上で述べたベクトルポテンシャルの時と同じ方法で，この式の解$V$を求めると次のようになります．

$$
V(\bm{r},t)
= \cfrac{1}{4 \pi \epsilon}
\int \cfrac{ \rho\left( \bm{r'},t-\frac{|\bm{r-r'}|}{v} \right) }{|\bm{r-r'}|} \bm{dr'} \tag{15}
$$

このスカラーポテンシャル$V$は，遅延ベクトルポテンシャルと同様，遅延スカラーポテンシャルと言います．

複素ベクトル表示（周波数領域）

式(12)の遅延ベクトルポテンシャル，式(15)の遅延スカラーポテンシャルは

\begin{eqnarray}
\begin{cases}
A_x(\bm{r},t)
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            i_x \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| } \\
A_y(\bm{r},t)
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            i_y \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| } \\
A_z(\bm{r},t)
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            i_z \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| }
\end{cases}
\tag{再掲12}
\end{eqnarray}

$$
V(\bm{r},t)
= \cfrac{1}{4 \pi \epsilon}
\int \cfrac{ \rho\left( \bm{r'},t-\frac{|\bm{r-r'}|}{v} \right) }{|\bm{r-r'}|} \bm{dr'} \tag{再掲15}
$$

時間領域の表示ですね．もし，電磁界が角周波数$\omega$で正弦波振動する場合は，これらの式を複素ベクトル表示できます．まず，式(12)について，電流の時刻$t-(|\bm{r-r'}|/v)$であり，$|\bm{r-r'}|/v$が時間の遅延ですね．ここで，角周波数と（遅延）時間の積が位相になりますから，

$$
- \omega \cfrac{|\bm{r-r'}|}{v}
= - 2 \pi \cfrac{|\bm{r-r'}|}{\lambda}
= - k |\bm{r-r'}|
$$

が位相になります．ここで，$k=2\pi/ \lambda$は第5回でも述べた波数（単位距離あたりの位相変化量）です．これを用いて，式(12)を周波数領域で表示する複素ベクトル表示にすると，次のようになります．

\begin{eqnarray}
\begin{cases}
A_x(\bm{r})
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{
            |\jiko{I}_x(\bm{r})|
            e^{-jk|\bm{r-r'}|}
        }{ |\bm{r-r'}| } \bm{dr'} \\
A_y(\bm{r})
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            |\jiko{I}_y(\bm{r})|
            e^{-jk|\bm{r-r'}|}
        }{ |\bm{r-r'}| }  \bm{dr'} \\
A_z(\bm{r})
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            |\jiko{I}_z(\bm{r})|
            e^{-jk|\bm{r-r'}|}
        }{ |\bm{r-r'}| } \bm{dr'}
\end{cases}
\tag{13}
\end{eqnarray}

同様に，遅延スカラーポテンシャルの複素ベクトル表示は次のようになります．

$$
V(\bm{r})
= \cfrac{1}{4 \pi \epsilon}
\int \cfrac{ |\dot{\rho}(\bm{r'})| e^{-jk|\bm{r-r'}|} }{|\bm{r-r'}|} \bm{dr'} \tag{16}
$$

まとめ

電磁界を求める際，ポテンシャルの方程式の解は次のようになります．

・スカラーポテンシャル
$$
V(\bm{r},t)
= \cfrac{1}{4 \pi \epsilon}
\int \cfrac{ \rho\left( \bm{r'},t-\frac{|\bm{r-r'}|}{v} \right) }{|\bm{r-r'}|} \bm{dr'}
$$

電磁界が角周波数$\omega$で振動する場合の複素ベクトルは次のようになります．

$$
V(\bm{r})
= \cfrac{1}{4 \pi \epsilon}
\int \cfrac{ |\dot{\rho}(\bm{r'})| e^{-jk|\bm{r-r'}|} }{|\bm{r-r'}|} \bm{dr'}
$$

・遅延ベクトルポテンシャル

\begin{eqnarray}
\begin{cases}
A_x(\bm{r},t)
  &= \displaystyle \cfrac{\mu}{4\pi} \int 
        \cfrac{ 
            i_x \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| } \bm{dr'} \\
A_y(\bm{r},t)
  &= \cfrac{\mu}{4\pi} \int 
        \cfrac{ 
            i_y \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| } \bm{dr'} \\
A_z(\bm{r},t)
  &= \cfrac{\mu}{4\pi} \int 
        \cfrac{ 
            i_z \left(
              \bm{r'}, 
              t - \frac{ |\bm{r-r'}| }{t} 
            \right)
        }{ |\bm{r-r'}| } \bm{dr'}
\end{cases}
\end{eqnarray}

電磁界が角周波数$\omega$で振動する場合の複素ベクトルは次のようになります．

\begin{eqnarray}
\begin{cases}
A_x(\bm{r})
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{
            |\jiko{I}_x(\bm{r})|
            e^{-jk|\bm{r-r'}|}
        }{ |\bm{r-r'}| } \bm{dr'} \\
A_y(\bm{r})
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            |\jiko{I}_y(\bm{r})|
            e^{-jk|\bm{r-r'}|}
        }{ |\bm{r-r'}| }  \bm{dr'} \\
A_z(\bm{r})
  &= \cfrac{\mu}{4\pi} \ds\int 
        \cfrac{ 
            |\jiko{I}_z(\bm{r})|
            e^{-jk|\bm{r-r'}|}
        }{ |\bm{r-r'}| } \bm{dr'}
\end{cases}
\end{eqnarray}

これらのポテンシャルを次の方程式に代入すれば，電磁界$\bm{E}$および$\bm{H}$が得られます．

\begin{eqnarray}
\begin{cases}
\bm{H} = \cfrac{1}{\mu} (\nabla \times \bm{A}) \\
\bm{E} = - \epsilon \pcfrac{\bm{A}}{t} - \epsilon \nabla V 
\end{cases}
\end{eqnarray}
1
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
2