深層学習Day３，Day４

深層学習Day3

Section1)　再帰型ニューラルネットワークの概念

§　RNNとは 　　時系列データに対応可能な、ニューラルネットワーク

§　時系列データ
　　時間的順序を追って一定間隔ごとに観察され，しかも相互に統計的依存関係が
　　認められるようなデータの系列
　　Ex.) 音声データ・テキストデータなど

　◆　RNNの全体像
　　　
　◆　RNNの数学的記述
　　　$u^t=W_{(in)}x^t+Wz^{t-1}+b$
　　　　u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
　　　$z^t=f(W_{in}x^t+Wz^{t-1}+b)　f$ は活性化関数
　　　　z[:,t+1] = functions.sigmoid(u[:,t+1])
　　　$v^t=W_{(out)}z^t+c$
　　　　np.dot(z[:,t+1].reshape(1, -1), W_out)
　　　$y^t=g(W_{(out)}z^t+c)　g$ は活性化関数
　　　　y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))

　◇　確認テスト
　　　○　RNNのネットワークには大きくわけて3つの重みがある。
　　　　1つは入力から現在の中間層を定義する際にかけられる重み、
　　　　1つは中間層から出力を定義する際にかけられる重みである。
　　　　残り1つの重みについて説明せよ。
　　　　→　前の中間層からの次の中間層へ至る際にかけられる重み

§　RNNの特徴
　　時系列モデルを扱うには、初期の状態と過去の時間t-1の状態を保持し、
　　そこから次の時間でのtを再帰的に求める再帰構造が必要になる。

　◇　演習チャレンジ
　　　以下は再帰型ニューラルネットワークにおいて構文木を入力として
　　　再帰的に文全体の表現ベクトルを得るプログラムである。ただし、
　　　ニューラルネットワークの重みパラメータはグローバル変数として
　　　定義してあるものとし、_activation関数はなんらかの活性化関数であるとする。
　　　木構造は再帰的な辞書で定義してあり、rootが最も外側の辞書であると仮定する。
　　　（く）にあてはまるのはどれか。

　　○　木構造とは
　　　　隣接した単語(表現ベクトル)から新たな表現ベクトルを
　　　　木のような構造をとりながら（下図）作っていき、
　　　　最後は１つの表現ベクトルとなる。

　　→　隣接した単語(表現ベクトル)から新たな表現ベクトルを作る際に、
　　　　それまでの表現ベクトルを保ちながら新たな表現ベクトルを作る必要がある。
　　　　【答え】（2）W.dot(np.concatenate([left, right]))

　◆　ＢＰＴＴ
　　§　BPTTとは
　　　　Backpropagation through timeの略
　　　　RNNにおいてのパラメータ調整方法の一種で誤差逆伝播の一種
　　§　誤差逆伝播法
　　　　計算結果（=誤差）から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる。
　◇　確認テスト
　　　連鎖律の原理を使い、dz/dxを求めよ。
　 　　$z=t^2$
　 　　$t=x+y$
　 　　→　$\frac{\partial z}{\partial t}\frac{\partial t}{\partial x}$
　 　　→　$\frac{\partial z}{\partial t}=2t，\frac{\partial t}{\partial x}=1$
　 　　→　$\frac{d z}{dx}=2t×1=2t=2(x+y)$

　◆　BPTTの数学的記述1
　　　$\frac{\partial E}{\partial W_{(in)}}=\frac{\partial E}{\partial u^t}\left[\frac{\partial u^t}{\partial W_{(in)}}\right]^T=\delta^t[x^t]^T$
　　　$\frac{\partial E}{\partial W_{(out)}}=\frac{\partial E}{\partial v^t}\left[\frac{\partial v^t}{\partial W_{(out)}}\right]^T=\delta^{out,t}[z^t]^T$
　　　$\frac{\partial E}{\partial W}=\frac{\partial E}{\partial u^t}\left[\frac{\partial u^t}{\partial W}\right]^T=\delta^t[z^{t-1}]^T$
　　　$\frac{\partial E}{\partial b}=\frac{\partial E}{\partial u^t}\frac{\partial u^t}{\partial b}=\delta^t$
　　　$\frac{\partial E}{\partial c}=\frac{\partial E}{\partial v^t}\frac{\partial v^t}{\partial c}=\delta^{out,t}$

　　　●　数式とコード
　　　　　$\frac{\partial E}{\partial W_{(in)}}=\frac{\partial E}{\partial u^t}\left[\frac{\partial u^t}{\partial W_{(in)}}\right]^T=\delta^t[x^t]^T$
　　　　　np.dot(X.T, delta[:,t].reshape(1,-1))
　　　　　$\frac{\partial E}{\partial W_{(out)}}=\frac{\partial E}{\partial v^t}\left[\frac{\partial v^t}{\partial W_{(out)}}\right]^T=\delta^{out,t}[z^t]^T$
　　　　　np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
　　　　　$\frac{\partial E}{\partial W}=\frac{\partial E}{\partial u^t}\left[\frac{\partial u^t}{\partial W}\right]^T=\delta^t[z^{t-1}]^T$
　　　　　np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))

　◆　BPTTの数学的記述2
　　　$u^t=W_{(in)}x^t+Wz^{t-1}+b$
　　　$z^t=f(W_{(in)}x^t+Wz^{t-1}+b)$
　　　$v^t=W_{(out)}z^t+c$
　　　$y^t=g(W_{(out)}z^t+c)$

　　　●　数式とコード
　　　　$u^t=W_{(in)}x^t+Wz^{t-1}+b$
　　　　u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
　　　　$z^t=f(W_{(in)}x^t+Wz^{t-1}+b)$
　　　　z[:,t+1] = functions.sigmoid(u[:,t+1])
　　　　$v^t=W_{(out)}z^t+c$
　　　　np.dot(z[:,t+1].reshape(1, -1), W_out)
　　　　$y^t=g(W_{(out)}z^t+c)$
　　　　y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))

　◇　確認テスト
　　　下図のy1をx・s0・s1・win・w・woutを用いて数式で表せ。
　　　※バイアスは任意の文字で定義せよ。
　　　※また中間層の出力にシグモイド関数g(x)を作用させよ。
　　　⇒　$y_1=g(W_{out}×s_1+c)$
　　　　　$s_1=W_{in}×x_1+W×s_0+b$

　◆　BPTTの数学的記述3
　　　$\frac{\partial E}{\partial u^t}=\frac{\partial E}{\partial v^t}\frac{\partial v^t}{\partial u^t}=\frac{\partial E}{\partial v^t}\frac{\partial\{W_{(out)}f(u^t)+c\}}{\partial u^t}=f'(u^t)W^T_{(out)}\delta^{out,t}=\delta^t$
　　　delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T))
　　　　　　　　　　　　　　　　　　　　　　 * functions.d_sigmoid(u[:,t+1])
　　　$\delta^{t-1}=\frac{\partial E}{\partial u^{t-1}}=\frac{\partial E}{\partial u^t}\frac{\partial u^t}{\partial u^{t-1}}=\delta^t$ $\left\{\frac{\partial u^t}{\partial z^{t-1}}\frac{\partial z^{t-1}}{\partial u^{t-1}}\right\}=\delta^t\left\{Wf'(u^{t-1})\right\}$
　　　$\delta^{t-z-1}=\delta^{t-z}\left\{Wf'(u^{t-z-1})\right\}$
　　　delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T))
　　　　　　　　　　　　　　　　　　　　　　 * functions.d_sigmoid(u[:,t+1])
　　　※　表記方法が正しいかどうかは分からないが以下の図より考えると分かりやすい

　◆　パラメータの更新式
　　　●　入力から中間層に至る重み
　　　　$W_{(in)}^{t+1}=W^t_{(in)}-\epsilon\frac{\partial E}{\partial W_{(in)}}=W^t-\epsilon \displaystyle\sum^{T_t}_{z=0}\delta^{t-z}\left[x^{t-z}\right]^T$
　　　　W_in -= learning_rate * W_in_grad

　　　●　前の中間層から今回の中間層に至る重み
　　　　$W_{(out)}^{t+1}=W^t_{(out)}-\epsilon\frac{\partial E}{\partial W_{(out)}}=W^t_{(out)}-\epsilon \delta^{out,t}\left[z^t\right]^T$
　　　　W_out -= learning_rate * W_out_grad

　　　●　中間層から出力に至る重み
　　　　$W^{t+1}=W^t-\epsilon\frac{\partial E}{\partial W}=W^t-\epsilon \displaystyle\sum^{T_t}_{z=0}\delta^{t-z}\left[z^{t-z-1}\right]^T$
　　　　W -= learning_rate * W_grad

　　　●　入力から中間層に至るバイアス
　　　　$b^{t+1}=b^t-\epsilon\frac{\partial E}{\partial b}=b^t-\epsilon\displaystyle\sum^{T_t}_{z=0}\delta^{t-z}$

　　　●　中間層から出力に至るバイアス
　　　　$c^{t+1}=c^t-\epsilon\frac{\partial E}{\partial c}=c^t-\epsilon\delta^{out,t}$

　　　※　中間層に至るまでは、前の時間の情報を引き継いで持っているため
　　　　　時間的な遡りを考慮　→　式中に$\sum$がある
　　　※　最新の中間層では前の時間までの情報は処理されているため
　　　　　時間的な遡りの考慮は不要　→　式中に$\sum$がない

　◆　BPTTの全体像
　　　$E^t=loss(y^t,d^t)$
　　　$,,,,,,,,,=loss\left(g(W_{(out)}z^t+c),d^t\right)$
　　　$,,,,,,,,,=loss\left(g(W_{(out)}f\left(W_{(in)}x^t+Wz^{t-1}+b)+c\right),d^t\right)$
　　　$W_{(in)}x^t+Wz^{t-1}+b$の部分
　　　⇒$W_{(in)}x^t+Wf(u^{t-1})+b$
　　　⇒$W_{(in)}x^t+Wf(W_{(in)}x^{t-1}+Wz^{t-2})+b)+b$
　　　と、式を展開していくと$z$のインデックスが時間を遡っていく。
　　　これは過去の時間からの情報がＲＮＮの中で蓄えられていることを示している。

　◇　コード演習問題
　　　左の図はBPTTを行うプログラムである。
　　　なお簡単化のため活性化関数は恒等関数であるとする。
　　　また、calculate_dout関数は損失関数を出力に関して偏微分した値を返す
　　　関数であるとする。
　　　（お）にあてはまるのはどれか。
　　　⇒　2）delta_t.dot(U)
　　　　　delta_tは（お）より上の行で損失関数の出力値に関する偏微分値(do)と
　　　　　V(おそらく出力層の活性化関数を通す前の値)とのドット積が
　　　　　設定されているので、１単位時間前の中間層へ誤差逆伝播を行うには
　　　　　中間層であるUとのdot積をとる

Section2)　ＬＳＴＭ

　◆　RNNの課題 　　　時系列を遡れば遡るほど、勾配が消失していくため、長い時系列の学習が困難 　　　⇒　解決策 　　　　　活性化関数の選択、重みの初期値設定、バッチ正規化などとは別で、 　　　　　ネットワークの構造自体を変えて解決したものがLSTM 　　　§　勾配消失問題 　　　　誤差逆伝播法が下位層に進んでいくに連れて、勾配がどんどん緩やかになっていく。 　　　　そのため、勾配降下法による、更新では下位層のパラメータはほとんど変わらず、 　　　　訓練は最適値に収束しなくなる。 　◇　確認テスト 　　　　シグモイド関数を微分した時、入力値が0の時に最大値をとる。 　　　　その値として正しいものを選択肢から選べ。 　　　　⇒　（2）0.25 　 　◆　勾配爆発 　　　　勾配が、層を逆伝播するごとに指数関数的に大きくなっていく

　◇　演習チャレンジ
　　　さ）にあてはまるのはどれか。
　　　⇒　（1）gradient * rate
　　　　　　rate = threshold / norm　←　rateは（gradientより求めた）ノルムに対して
　　　　　　しきい値が何倍かを表しているので、そのrateをgradientに掛ける
　　　　　　※　np.linalg.normはベクトルの大きさ（ノルム）を計算する関数
　◆　LSTMの全体図
　　　LSTMはRNNの１種
　　　青い点線が時間のループ
　　　黒い点線で囲まれている範囲が中間層

　　　●　CEC
　　　　　・　勾配消失および勾配爆発の解決方法（※１）として導入された
　　　　　・　CECは記憶機能のみ　→　入力データについて、時間依存度に関係なく
　　　　　　　重みが一律
　　　　　※１　勾配が1であれば解決できるので勾配を１にする
　　　●　入力ゲート
　　　　　・　CECにどのように入力データを覚えてもらうかを指示
　　　　　・　CECにどのように入力データを覚えさせるかを学習する
　　　●　出力ゲート
　　　　　・　CECが覚えているデータをどのように使うかを指示
　　　　　・　CECの覚えているデータをどのように使うかを学習する
　　　●　忘却ゲート
　　　　　・　CECの覚えているデータどれを忘れさせるかを指示
　　　　　・　過去の情報が要らなくなった場合、そのタイミングで情報を忘却する機能
　　　●　図中の$W$は各ゲートで今回の入力をどれくらい判断材料として使うか
　　　　　$U$は各ゲートで前回の出力をどれくらい判断材料として使うかを決める
　　　●　入力・出力ゲートを追加することで、それぞれのゲートへの入力値の重みを、
　　　　　重み行列W,Uで可変可能とする。CECの課題を解決。
　　　●　図中真ん中下部の赤枠内の数式
　　　　　$c(t)=i(t)・a(t) + f(t)・c(t-1)$
　　　　　$c(t)$：今回のCECの状態
　　　　　$i(t)$：入力ゲートより今回の情報をCECがどれくらい覚えるかの指示
　　　　　$a(t)$：活性化関数を通って出てきた入力情報
　　　　　$f(t)$：忘却ゲートどれくらい覚えておくのか、忘れるのかの指示
　　　　　$c(t-1)$：前回の情報

　　　◇　確認テスト
　　　　　以下の文章をLSTMに入力し空欄に当てはまる単語を予測したいとする。
　　　　　文中の「とても」という言葉は空欄の予測においてなくなっても
　　　　　影響を及ぼさないと考えられる。このような場合、
　　　　　どのゲートが作用すると考えられるか。
　　　　　「映画おもしろかったね。ところで、とてもお腹が空いたから何か____。」
　　　　　⇒　忘却ゲート

　　　◇　演習チャレンジ
　　　　　以下のプログラムはLSTMの順伝播を行うプログラムである。
　　　　　ただし_sigmoid関数は要素ごとにシグモイド関数を作用させる関数である。
　　　　　（け）にあてはまるのはどれか。
　　　　　⇒　（3）input_gate * a + forget_gate * c
　　　　　　　　（け）の前後より
　　　　　　　　a：入力データにシグモイド関数を作用させた値
　　　　　　　　c：シグモイド関数を作用させた後、出力ゲートを作用させる値
　　　　　　　　と読み取れるため、cに入る値が推測される　
　
　　　●　覗き穴結合
　　　　　CEC自身の値は、ゲート制御に影響を与えていないが、
　　　　　CEC自身の値に、重み行列を介して伝播可能にした構造。
　　　　　※　あまり大きな改善効果は見られていない

Section3)　ＧＲＵ

　§　LSTMの課題であるパラメータ数が多く、計算負荷が高くなるという問題を解消したもの

　　◆　GRUの全体像

　　　●　リセットゲート
　　　　・　隠れ層の状態をどのような状態で保持しておくかを制御する
　　　●　更新ゲート
　　　　・　前回の記憶と今回の記憶をもとに、どのように今回の出力を得るかを制御する
　　　●　図中真ん中下部の赤枠内
　　　　　隠れ層として計算状態を保存しておく計算式

　　◇　確認テスト
　　　　LSTMとCECが抱える課題について、それぞれ簡潔に述べよ。
　　　　⇒　LSTMはパラメータ数が多く、計算量が多い
　　　　　　CECは常に勾配が１であり学習能力がない

　　◇　演習チャレンジ
　　　　GRU(Gated Recurrent Unit)もLSTMと同様にRNNの一種であり、
　　　　単純なRNNにおいて問題となる勾配消失問題を解決し、
　　　　長期的な依存関係を学習することができる。
　　　　LSTMに比べ変数の数やゲートの数が少なく、
　　　　より単純なモデルであるが、タスクによってはLSTMより良い性能を発揮する。
　　　　以下のプログラムはGRUの順伝播を行うプログラムである。
　　　　ただし_sigmoid関数は要素ごとにシグモイド関数を作用させる関数である。
　　　　（こ）にあてはまるのはどれか。
　　　　⇒　（4）(1-z) * h + z * h_bar
　　　　　　zは更新ゲート、hは今回の中間表現、h_barは前回の中間表現

　　◇　確認テスト
　　　　LSTMとGRUの違いを簡潔に述べよ
　　　　⇒　LSTMには入力ゲート、出力ゲート、忘却ゲート、CECがあるが
　　　　　　GRUにはなく、更新ゲートとリセットゲートがある。
　　　　　　LSTMはパラメータが多く、GRUはパラメータが少ない。
　　　　　　結果的にLSTMよりGRUの方が計算量が少ない。
　　　　　　

Section4)　双方向RNN

　§　過去の情報だけでなく、未来の情報を加味することで、 　　　精度を向上させるためのモデル 　　　※　実用例 　　　　　文章の推敲や、機械翻訳等 

　　◇　演習チャレンジ
　　　　以下は双方向RNNの順伝播を行うプログラムである。順方向については、
　　　　入力から中間層への重みW_f, 一ステップ前の中間層出力から中間層への重みをU_f、
　　　　逆方向に関しては同様にパラメータW_b, U_bを持ち、
　　　　両者の中間層表現を合わせた特徴から出力層への重みはVである。
　　　　_rnn関数はRNNの順伝播を表し中間層の系列を返す関数であるとする。
　　　　（か）にあてはまるのはどれか
　　　　⇒　（4）np.concatenate([h_f, h_b[::-1]], axis=1)
　　　　　　順方向と逆方向で同じ時間の値は同じ場所に入るように axis=1で配列を結合し
　　　　　　特徴量を失わずに１つの特徴ベクトルを得ている

Section5)　seq2seq

　§　Seq2seqとは 　　　・　系列(Sequence)を入力として、系列を出力するもの 　　　・　入力系列がEncode(内部状態に変換)され、内部状態からDecode(系列に変換)する 　　　・　Encoder-Decoderモデルの一種 　　　・　機械対話や、機械翻訳などに使用されている 

　　◆　全体図

　　◆　Encoder RNN
　　　　ユーザーがインプットしたテキストデータを、単語等のトークンに区切って
　　　　渡す構造。
　　　　Taking :文章を単語等のトークン毎に分割し、トークンごとのIDに分割する。
　　　　Embedding :IDから、そのトークンを表す分散表現ベクトル
　　　　　　　　　(単語の意味を抽出したベクトル)に変換。
　　　　　　　　　IDよりも少ない種類になるように変換する。
　　　　　　　　　単語の意味が似ているものはEmbedding表現の数字の並びが似るように
　　　　　　　　　機械学習などにより学習させて変換する。
　　　　Encoder RNN:ベクトルを順番にRNNに入力していく。

　　　●　処理手順
　　　　・　１つ目のベクトル(vec1)をRNNに入力し、hidden stateを出力。
　　　　　　このhiddenstateと次の入力vec2をまたRNNに入力してきた
　　　　　　hidden stateを出力という流れを繰り返す。
　　　　・　最後のvecを入れたときのhiddenstateをfinalstateとしてとっておく。
　　　　　　このfinalstateがthoughtvectorと呼ばれ、入力した文の意味を表す
　　　　　　ベクトルとなる
　　◆　Decoder RNN
　　　　システムがアウトプットデータを、単語等のトークンごとに生成する構造。
　　　●　処理手順
　　　　１．Decoder RNN: Encoder RNN のfinal state (thought vector) から、
　　　　　　各token の生成確率を出力していきます
　　　　　　final state をDecoder RNN のinitial state ととして設定し、Embedding を入力
　　　　２．Sampling:生成確率にもとづいてtoken をランダムに選びます。
　　　　３．Embedding:2で選ばれたtoken をEmbedding してDecoder RNN への
　　　　　　次の入力とします。
　　　　４．Detokenize:1 -3 を繰り返し、2で得られたtoken を文字列に直します。

　　◇　確認テスト
　　　　下記の選択肢から、seq2seqについて説明しているものを選べ。
　　　　⇒　（2）RNNを用いたEncoder-Decoderモデルの一種であり、
　　　　　　　　機械翻訳などのモデルに使われる。
　　　　（1）は双方向RNN
　　　　（3）は構文木
　　　　（4）はLSTM

　　◇　演習チャレンジ
　　　　機械翻訳タスクにおいて、入力は複数の単語から成る文（文章）であり、
　　　　それぞれの単語はone-hotベクトルで表現されている。
　　　　Encoderにおいて、それらの単語は単語埋め込みにより特徴量に変換され、
　　　　そこからRNNによって（一般にはLSTMを使うことが多い）
　　　　時系列の情報をもつ特徴へとエンコードされる。
　　　　以下は、入力である文（文章）を時系列の情報をもつ特徴量へとエンコードする
　　　　関数である。ただし_activation関数はなんらかの活性化関数を表すとする。
　　　　（き）にあてはまるのはどれか。
　　　　⇒　（1）E.dot(w)
　　　　　　E(embed_size, vocab_size)、w(vocab_size)から計算できるdot積は(1)になる
　　　　　　(4)のスカラーとしての掛け算はここではおかしいと思う
　　
　　◆　Seq2seqの課題
　　　　一問一答しかできない
　　　　問に対して文脈も何もなく、ただ応答が行われる続ける。

　　◆　HRED
　　　　§　HREDとは
　　　　　・　過去n-1 個の発話から次の発話を生成する
　　　　　・　Seq2seqよりも人間らしい文章が生成される
　　　　　・　Seq2Seq　+ Context RNN（Encoder のまとめた各文章の系列をまとめて
　　　　　　　これまでの会話コンテキスト全体を表すベクトルに変換する構造）
　　　　●　HREDの課題
　　　　　・　確率的な多様性が字面にしかなく、会話の「流れ」のような多様性が無い。
　　　　　・　短く情報量に乏しい答えをしがち　

　　◆　VHRED
　　　　HREDに、VAEの潜在変数の概念を追加したもの

　　◇　確認テスト
　　　　seq2seq：１文の１問１答に対して処理ができるある時系列データから
　　　　　　　　別のある時系列データを作り出すネットワーク
　　　　HRED：seq2seqの機構にそれまでの文脈の意味ベクトルを
　　　　　　　解釈に加えられるようにすることで、
　　　　　　　文脈の意味をくみ取った文の変換（encodeとdecode）を
　　　　　　　できるようにしたもの
　　　　VHRED：HREDが文脈に対して当たり障りのない回答しか作成できない事の解決策
　　　　　　　　VAEの考え方を取り入れて、短い当たり障りのない単語以上の出力が
　　　　　　　　できるように改良を施したモデル

　　◆　オートエンコーダ
　　　●　教師なし学習の一つ。
　　　　　そのため学習時の入力データは訓練データのみで教師データは利用しない。
　　　●　MNISTの場合、28x28の数字の画像を入れて、
　　　　　同じ画像を出力するニューラルネットワーク（下図）
　　　●　メリットととして次元削減が行える

　　◆　VAE
　　　　通常のオートエンコーダーの場合、何かしら潜在変数z（上図）に
　　　　データを押し込めているものの、その構造がどのような状態かわからない。
　　　　VAEはこの潜在変数zに確率分布z∼N(0,1)を仮定したもの。
　　　　このようにすることで形の似た画像は同じようなベクトルになるように
　　　　潜在変数ｚが学習される

　　◇　確認テスト
　　　　VAEに関する下記の説明文中の空欄に当てはまる言葉を答えよ。
　　　　自己符号化器の潜在変数に____を導入したもの。
　　　　⇒　確率分布

Section6)　word2vec

　　§　word2vecとは 　　　●　embedding表現を得る手法（単語をベクトル表現する手法）の１つ 　　　●　CBOW(Continuous Bag-of-Words Model)とskip-gramという２つのモデルがある 　　　　　CBOW：単語周辺の文脈から中心の単語を推定 　　　　　skip-gram：中心の単語からその文脈を構成する単語を推定 　　　　　推定の際にembedding表現を得る

　　　学習データからボキャブラリを作成すると辞書の単語数だけできあがる。
　　　これを、入力層のone-hotベクトル（ボキャブラリ数）×任意の単語ベクトル次元数の
　　　重み行列とすることで、大規模データの分散表現の学習を、
　　　現実的な計算速度とメモリ量で実現可能にした。　

Section7)　Attention Mechanism

　　§　Attention Mechanismとは 　　　　「入力と出力のどの単語が関連しているのか」の関連度を学習する仕組み

　　　seq2seq では、2単語でも、100単語でも、固定次元ベクトルの中に
　　　入力しなければならないため長い文章への対応が難しい。
　　　文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていく
　　　仕組みが必要になる。その解決策がAttention Mechanismであり
　　　文章より重要な単語を見分けて選択的に隠れ層の状態として用いて処理を行う。

　　◇　確認テスト
　　　　RNNとword2vec、seq2seqとAttentionの違いを簡潔に述べよ
　　　　⇒　RNNは時系列データ処理に適したニューラルネットワーク
　　　　　　word2vecは単語の分散表現を得る手法
　　　　　　seq2seqは１つの時系列データから別の時系列データを得るネットワーク
　　　　　　Attentionは時系列データのそれぞれの単語の関連性に重みをつける手法

実装演習

　3_1_simple_RNN_after.ipynb 　●　weight_init_stdを変更してみる 　　大きくしても、小さくしても収束しなくなり、 　　最初のweight_init_std=1がちょうど良かったと思われる  　●　learning_rateを変更してみる 　　大きくすると(0.5)収束が早くなった。小さくすると(0.05)収束が遅くなった  　●　hidden_layer_sizeを変更してみる 　　小さくすると(4)収束しなくなった（8も試したが、8のときは収束した） 　　大きくすると収束が早くなった  　●　重みの初期化方法を変更してみる 　　Xavierを用いると収束しなくなった。 　　Heを用いると収束が早くなった。 　　両者の結果の違いについて、元の重み＞Heを使った重み＞Xavierを使った重み 　　となっているので、試しにweight_init_stdをもとの値の 　　1より少しだけ小さい値にして試してみたところ、 　　weight_init_std=0.8にするとHeと似た結果となった。 　　（もっと小さくすると収束しなくなることはweight_init_stdの変更で確認済み） 　　ここではHeを使用することで重みが丁度よい具合になったのではないか。 　　Heはweight_init_std=0.8のように一律ではなく、前層のノード数の影響を受けるが 　　上記の考え方がおおよそで合っているのではないかと思う。  　●　活性化関数を変更してみる 　　収束しなくなった 　　ここまでで既にsigmoid関数を使用して収束することが確認できているので 　　RELUやtanhでは勾配が大きすぎるのではないかと思う。  　3_3_predict_sin.ipynb 　●　[try]に書かれている通りに変数を変更し、実行してみた 　　　maxlen=5、iters_num=3000で精度の良い予測になったが 　　　maxlenは５より増やすとかえって予測精度が落ち、 　　　またmaxlen=5の状態で、iters_num=4000にしても精度が落ちた。 　　　maxlenに関してはサインカーブという形状から 　　　横軸を大きくとりすぎても予測精度が落ちることも考えられるが 　　　iters_numを増やすと制度が落ちてくるのは分からない。 　　　実際の単語を扱うときも同じことが起きるのだろうか。 　　　興味深い点である。 

深層学習Day4

Section1) 強化学習

　§　強化学習とは 　　　長期的に報酬を最大化できるように環境のなかで行動を選択できる 　　　エージェントを作ることを目標とする機械学習の一分野 　　　行動の結果として与えられる利益(報酬)をもとに、 　　　行動を決定する原理を改善していく仕組み。

　　◆　イメージ

　　◆　強化学習の応用例
　　　　●　マーケティングの場合
　　　　　・　環境:会社の販売促進部
　　　　　・　エージェント:プロフィールと購入履歴に基づいて
　　　　　　　　　　　　　キャンペーンメールを送る顧客を決めるソフトウェア
　　　　　・　行動:顧客ごとに送信、非送信のふたつの行動を選ぶ
　　　　　・　報酬:キャンペーンのコストという負の報酬と
　　　　　　　　　　キャンペーンで生み出されると推測される売上という正の報酬を受ける
　　◆　探索と利用のトレードオフ
　　　　●　環境について事前に完璧な知識があれば、
　　　　　　最適な行動を予測し決定することは可能であるが
　　　　　　強化学習の場合、上記仮定は成り立たないとする。
　　　　　　不完全な知識を元に行動しながら、データを収集。最適な行動を見つけていく。
　　　　●　過去のデータで、ベストとされる行動のみを常に取り続ければ
　　　　　　他にもっとベストな行動を見つけることはできない（探索が足りない）
　　　　　　　　　　　　　　　　　↓↑
　　　　　　未知の行動のみを常に取り続ければ、過去の経験が活かせない
　　　　　　（利用が足りない）

　　◆　強化学習と通常の教師あり、教師なし学習との違い
　　　　●　目標が違う
　　　　　・　教師なし、あり学習では、データに含まれるパターンを見つけ出す
　　　　　　　およびそのデータから予測することが目標
　　　　　・　強化学習では、優れた方策を見つけることが目標

　　◆　価値関数
　　　　§　価値関数とは
　　　　　価値を表す関数としては、状態価値関数と行動価値関数の2種類がある

　　　　●　状態価値関数
　　　　　　環境の状態だけで価値が決まる

　　　　●　行動価値関数
　　　　　　状態とエージェントが採った行動の２つ情報
　　　　　　（どんな状態のときにどんな行動を採ったか）をもとに価値が決まる
　　　　　　
　　◆　方策関数
　　　　§　方策関数とは
　　　　　ある状態でエージェントがどんな行動を採るのかの確率を与える関数
　　　　　
　　　　方策関数：π(s)=a
　　　
　　◆　関数の関係
　　　　エージェントは方策に基づいて行動する
　　　　・　方策関数（$π(s)=a$）は、VやQを基にどういう行動をとるか
　　　　　　（経験を活かすorチャレンジするなど）その瞬間瞬間の行動をどうするか
　　　　・　$\left\{\begin{array}{ccc}V^π(s)：状態関数　　　　　　　　　　　　　　　　　　　　　　　　　\\Q^π(s,a)：行動価値関数（状態+行動関数）　　　　　　　　　　　\end{array}\right\}は、$
　　　　　ゴールまで今の方策を続けたときの報酬の予測値が得られる
　　　　　⇒　このまま続けたら最終的にどうなるかを考える
　　　　●　強化学習は"価値関数"と"方策関数"の２つが優秀ならうまくいく
　　　　　⇒　価値関数が将来のことを考えながら方策関数が今の行動を選べる

　　◆　方策勾配法
　　　　方策をモデル化して最適化する手法
　　　　$\theta^{(t+1)}=\theta^{(t)}+\epsilon\nabla J(\theta)$
　　　　$\theta$はニューラルネットワークでいう重み、tは時間、$\epsilon$は学習率、
　　　　$J(\theta)$はニューラルネットワークでは誤差関数、ここでは期待収益
　　　　ニューラルネットワークでは誤差を小さくするが強化学習では期待収益を大きくする
　　　　※　ニューラルネットワークの重みの更新式と違って＋であることに注意

　　　　§　$J(\theta)$のJとは
　　　　　●　方策の良さ
　　　　　●　Jの定義
　　　　　　・　平均報酬
　　　　　　・　割引報酬
　　　　　　上記の定義に対応して、行動価値関数:Q(s,a)の定義を行い
　　　　　　方策勾配定理が成り立つ
　　　　　　$\nabla_\theta J(\theta)=\mathbb E_{π_\theta}[(​\nabla _\theta logπ _\theta (a|s)Q^π(s,a))]$

　　　　　　もとの式：$\nabla_\theta J(\theta)=​\nabla _\theta \displaystyle\sum _ {a∈A} π _ \theta(a|s)Q^π(s,a)$を変形すると上記の式が得られる
　　　　　　
　　　　　　　　・　$π _ \theta(a|s)Q^π(s,a)$：ある行動をとるときの報酬

　　　　　　　　・　$\displaystyle\sum _ {a∈A}$：すべての行動における報酬をサマリー

Section2)　Alpha Go

　◆　Alpha Go (Lee) 　　●　PolicyNet（方策関数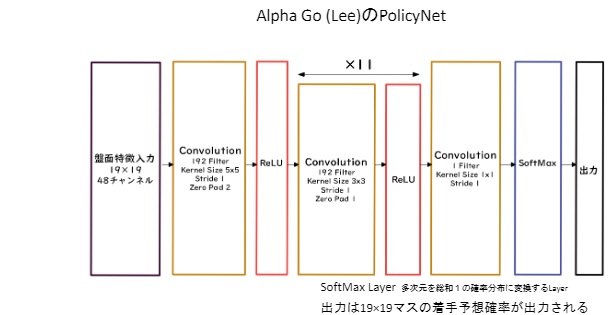）  　　●　ValueNet（価値関数）  　　●　Alpha Go の学習 　　　１、教師あり学習によるRollOutPolicyとPolicyNetの学習 　　　２、強化学習によるPolicyNetの学習 　　　３、強化学習によるValueNetの学習 　　　 　　●　RollOutPolicy 　　　・　PolicyNetよりも多少精度は落ちるが、高速な方策関数 　　　・　ニューラスルネットワークであるPolicyNetと異なり、線形の方策関数 　　　・　探索中に高速に着手確率を出すために使用される

　　●　モンテカルロ木探索
　　　・　コンピュータ囲碁ソフトでは現在もっとも有効とされている探索法
　　　・　価値観数を学習させるときに用いる
　　　・　RollOutPolicyを利用してモンテカルロ木探索を行う

　◆　AlphaGoZero
　　●　AlphaGo(Lee) との違い
　　　１、教師あり学習を一切行わず、強化学習のみで作成
　　　２、特徴入力からヒューリスティックな要素を排除し、石の配置のみにした
　　　３、PolicyNetとValueNetを１つのネットワークに統合した
　　　４、Residual Net（後述）を導入した
　　　５、モンテカルロ木探索からRollOutシミュレーションをなくした

　　●　PolicyNet（方策関数）とValueNet（価値関数）が途中で枝分かれしている

　　●　ResidualNetwork
　　　・　ネットワークにショートカット構造を追加して、
　　　　　勾配の爆発、消失を抑える効果を狙ったもの
　　　　　そのおかげで深いネットワークでも安定した学習が可能

　　●　ResidualNetworkの派生形
　　　【Residual Blockの工夫】
　　　　・　Bottleneck：1×1KernelのConvolutionを利用し、
　　　　　　　　　　１層目で次元削減を行って3層目で次元を復元する３層構造にし、
　　　　　　　　　　２層のものと比べて計算量はほぼ同じだが１層増やせるメリットが
　　　　　　　　　　あるとしたもの
　　　　・　PreActivation ：ResidualBlockの並びを
　　　　　　　　　　　　　BatchNorm→ReLU→Convolution→BatchNorm→ReLU→Convolution→Add
　　　　　　　　　　　　　とすることにより性能が上昇したとするもの
　　　【Network構造の工夫】
　　　　・　WideResNet：ConvolutionのFilter数をk倍にしたResidual Network
　　　　・　PyramidNet：各層でFilter数を増やしていくResidual Network

Section3)　軽量化・高速化技術

◆　分散深層学習による高速化 　　§　分散深層学習とは 　　　　機械学習の計算量は毎年１０倍くらいのスピードで増えており 　　　　コンピュータの性能は１８か月で約２倍である 　　　　そのためコンピュータの台数を増やして機械学習を行うという手法

　【データ並列化】
　　・　親モデルを各ワーカー（コンピューターor演算機）に子モデルとしてコピー
　　・　データを分割し、各ワーカーごとに計算させる

　　●　データ並列化: 同期型
　　　　各ワーカーが計算が終わるのを待ち、全ワーカーの勾配が出たところで
　　　　勾配の平均を計算し、親モデルのパラメータを更新する。

　　●　データ並列化: 非同期型
　　　　各ワーカーはお互いの計算を待たず、各子モデルごとに更新を行う。
　　　　学習が終わった子モデルはパラメータサーバにPushされる。
　　　　新たに学習を始める時は、パラメータサーバからPopしたモデルに対して
　　　　学習していく。

　　●　同期型と非同期型の比較
　　　・　処理のスピードは、お互いのワーカーの計算を待たない
　　　　　非同期型の方が早い。
　　　・　非同期型は最新のモデルのパラメータを利用できないので
　　　　　学習が不安定になりやすい。
　　　・　現在は同期型の方が精度が良いことが多いので、主流となっている。

　【モデル並列化】
　　　・　親モデルを各ワーカーに分割し、それぞれのモデルを学習させる。
　　　　　全てのデータで学習が終わった後で、一つのモデルに復元。
　　　・　枝分かれしたモデルを分割することが多い。
　　　・　データ並列化はコンピュータを複数台使って学習させることが多く
　　　　　モデル並列化は１台のコンピュータ内に演算機を複数設置して
　　　　　学習させることが多い
　　　・　モデルのパラメータ数が多いほど、スピードアップの効率も向上する。
　　　モデルが大きい時はモデル並列化を、データが大きい時はデータ並列化をすると良い。

◆　GPUによる高速化
　　●　GPGPU (General-purpose on GPU)
　　　・　元々の使用目的であるグラフィック以外の用途で使用されるGPUの総称
　　●　CPU
　　　・　高性能なコアが少数
　　　・　複雑で連続的な処理が得意
　　●　GPU（ニューラルネットワークの学習に向いている）
　　　・　比較的低性能なコアが多数
　　　・　簡単な並列処理が得意
　　　・　ニューラルネットの学習は単純な行列演算が多いので、高速化が可能
　　●　GPGPU開発環境
　　　・　CUDA
　　　・　OpenCL
　　　※　Deep Learningフレームワーク(Tensorflow, Pytorch)内で実装されているので、
　　　　　使用する際は指定すれば良い

　◆　軽量化
　　　代表的な手法として以下の３つがある
　　　・量子化
　　　・蒸留
　　　・プルーニング

◆　量子化
　　　モデルの軽量化の手法として簡単であるのでよく使用される
　　　重みの精度を下げることにより計算の高速化と省メモリ化を行う技術
　　●　手法　
　　　通常のパラメータの64 bit 浮動小数点を32 bit など下位の精度に落とすことで
　　　メモリと演算処理の削減を行う
　　●　メリット、デメリット
　　　・メリット
　　　　計算の高速化
　　　　省メモリ化
　　　　計算量が少ない
　　　・デメリット
　　　　精度の低下
　　※　実際の問題では倍精度を単精度にしてもほぼ精度は変わらず
　　　　計算速度は約倍になる
　　　　ただし極端な量子化を行うと精度が落ちてしまうので
　　　　精度が落ちない程度に量子化をする必要がある

◆　蒸留
　　　複雑で精度の良い教師モデルから軽量な生徒モデルを効率よく学習を行う技術
　　　学習済みの精度の高いモデルの知識を軽量なモデルへ継承させる
　　　・　教師モデル
　　　　　予測精度の高い、複雑なモデルやアンサンブルされたモデル
　　　・　生徒モデル
　　　　　教師モデルをもとに作られる軽量なモデル
　　　教師モデルの重みを固定し生徒モデルの重みを更新していく
　　　誤差は教師モデルと生徒モデルのそれぞれの誤差を使い重みを更新していく
　　　
　　　※　転移学習との違い
　　　　　転移学習は既に学習済みのモデルを使って別の問題を解くことで
　　　　　蒸留は既に学習済みのモデルを使ってコンパクトなモデルを実現すること

◆　プルーニング
　　　モデルの精度に寄与が少ないニューロンを削減することでモデルの軽量化、
　　　高速化をする
　　　・　ニューロンの削減手法
　　　　　重みが閾値以下の場合ニューロンを削減し、再学習を行う
　　　かなりのニューロンを削減しても制度はあまり変わらないことが分かっている

Section4)　応用技術

　◆　MobileNet(画像を認識するネットワーク) 　　　一般的な畳み込みレイヤーは計算量が多い 　　　MobileNetsはDepthwise ConvolutionとPointwise Convolutionの組み合わせで 　　　軽量化を実現 　　　現在ではMobileNetは第１世代～第３世代まである。 　●　一般的な畳み込みレイヤーは下図のとおりであり、出力マップ全体の計算量は 　　　$H×W×K×K×C×M$となる 

　●　Depthwise Convolution
　　　フィルタ数＝１（固定）
　　　１チャンネルごとにしか畳み込みを行わない
　　　入力マップのチャンネル数＝出力マップのチャンネル数
　　　とすることで計算量が大幅に削減され
　　　$H×W×K×K×C$となる
　　　各層ごとの畳み込みなので層間の関係性は全く考慮されないため
　　　通常はPointwise Convolutionとセットで使うことで解決

　●　Pointwise Convolution
　　　カーネルサイズ＝１×１（固定）
　　　フィルタ数＝出力マップのチャンネル数
　　　出力マップ(チャネル数)はフィルタ数分だけ作成可能(任意のサイズが指定可能)
　　　計算量は
　　　$H×W×C×M$となる

　●　MobileNetのアーキテクチャ
　　　通常の畳込みが空間方向とチャネル方向の計算を同時に行うのに対して、
　　　Depthwise Separable ConvolutionではそれらをDepthwise Convolutionと
　　　Pointwise Convolutionと呼ばれる演算によって個別に行う。
　　　普通の畳み込みでは$H×W×K×K×C×M$であった計算量が
　　　MobileNetでは$(H×W×K×K×C) + (H×W×C×M)$となる

　◆　DenseNet(画像を認識するネットワーク)
　　　CNNアーキテクチャの一種
　　　ニューラルネットワークでは層が深くなるにつれて、
　　　学習が難しくなるという問題があったが、
　　　ResNetなどのCNNアーキテクチャでは前方の層から
　　　後方の層へアイデンティティ接続を介して
　　　パスを作ることで問題を対処した。
　　　DenseBlockと呼ばれるモジュールを用いたDenseNetも
　　　そのようなアーキテクチャの一つである。

　　●　DenseNetとResNetの違い
　　　・　DenseBlockでは前方の各層からの出力全てが後方の層への入力として用いられる
　　　・　RessidualBlockでは前1層の入力のみ後方の層へ入力

　　●　成⻑率(Growth Rate)
　　　DenseNet内で使用されるDenseBlockと呼ばれるモジュールでは成⻑率(Growth Rate)
　　　と呼ばれるハイパーパラメータが存在する。
　　　DenseBlock内の各ブロック毎にk個ずつ特徴マップのチャネル数が増加していく時、
　　　kを成⻑率と呼ぶ

　◆　Layer正規化/Instance正規化
　　●　Batch Norm
　　　・　H x W x CのsampleがN個あった場合に、N個の同一チャネルが正規化の単位
　　　・　チャンネルごとに正規化された特徴マップを出力
　　　・　下図Batch Normの⻘い部分が正規化の単位
　　　ミニバッチのサイズを大きく取れない場合には、効果が薄くなってしまう。
　　●　Layer Norm
　　　・　N個のsampleのうち一つに注目。H x W x Cの全てのpixelが正規化の単位
　　　・　特徴マップごとに正規化された特徴マップを出力
　　　・　入力データのスケールに関してロバスト
　　　・　重み行列のスケールやシフトに関してロバスト
　　　・　下図Layer Normの⻘い部分が正規化の単位
　　　ミニバッチの数に依存しないので、上記の問題を解消できていると考えられる
　　●　Instance Nrom
　　　・　各sampleの各チャネルごとに正規化
　　　・　コントラストの正規化に寄与・画像のスタイル転送やテクスチャ合成タスク
　　　　　などで利用
　　　・　下図Instance Nromの⻘い部分が正規化の単位

　◆　Wavenet(音声生成モデル)
　　　時系列データに対して畳み込み（Dilated convolution）を適用する
　　　●　Dilated convolution
　　　・　層が深くなるにつれて畳み込むリンクを離す
　　　・　受容野を簡単に増やすことができる

　●　深層学習を用いて結合確率を学習する際に、効率的に学習が行える
　　　アーキテクチャを提案したことがWaveNet の大きな貢献の1 つである。
　　　提案された新しいConvolution 型アーキテクチャは（あ）と呼ばれ、
　　　結合確率を効率的に学習できるようになっている。
　　　（あ）⇒　Dilated causal convolution
　　　以外の説明
　　　○　Depthwise separable convolution
　　　　モバイルネットワークで使用するconvolutionの１つ　
　　　○　Pointwise convolution
　　　　モバイルネットワークで使用するconvolutionの１つ　
　　　○　Deconvolution
　　　　逆畳み込み
　　　　解像度を上げるときに使用する
　●　Dilated causal convolutionを用いた際の大きな利点は、
　　　単純なConvolution layer と比べて（い）ことである。
　　　（い）⇒　パラメータ数に対する受容野が広い

Section5)　Transformer

　§　Transformer 　　・　2017年に導入されたディープラーニングモデルで主に自然言語処理の分野で 　　　　使用される 　　・　RNNと同様に自然言語などの時系列データを処理するように設計されているが 　　　　RNNで用いる再帰、CNNで用いる畳み込みは使わない 　　・　Attention層のみで構築される 　　・　翻訳やテキストの要約など様々なタスクで利用可能 　　・　並列化が容易であり、訓練時間を大きく削減できる 　　・　ニューラル機械翻訳の問題点である「長さに弱い」を解消したモデル 　　・　BERTTはTransformerを使用している  　◆　Attention (注意機構) 　　情報量が多くなってきたときに何に注意を払って、何に注意を払わないかを 　　学習的に決定していく 　　　　$c_i=\displaystyle\sum^{T_x}_{j=1} \alpha _{ij} h_j$

　　　　$c_i$：アテンション（どこに注意を払うか）
　　　　$h_j$：単語の意味を表したベクトル
　　　　$\alpha_{ij}$：係数

　　　　$\alpha_{ij} = \frac {exp(e_{ij})} { \sum^{T_x}_{k=1} exp(e _{ik})}=softmax(e _{ij})$

　　　　　$\alpha_{ij}$を$j$について和を取ると１になる
　　　　　$c_i$は単語ベクトル$(h_j)$全てを、合計が１になるように重みを付けて和を取ったもの
　　　　　⇒　重みを制御して注意したい単語ベクトルを合計

　　　　$e_{ij}=a(s_{i-1},h_j)$
　　　　　$a$：活性化関数
　　　　　$s,h$：隠れ層
　　　　　
　　・　Attentionは何をしているのか
　　　　Attentionは辞書オブジェクトであり、query(検索クエリ)に一致するkeyを索引し、
　　　　対応するvalueを取り出す操作であると見做すことができる。
　　　　これは辞書オブジェクトの機能と同じである。
　 　　※　Attentionを使うと文長が長くなっても翻訳精度が落ちないことが確認されている

　◆　Transformer

　　●　Source Target Attention
　　　　Queryと類似度の高い（内積の大きい）Keyを検索しそのKeyに対応する
　　　　Valueを出力する
　　●　Self-Attention
　　　　自分自身をもとにQuery、Key、Valueの３つのベクトルを作成
　　　　処理対象データのQueryとその他のデータのKeyの内積と、そのsoftmaxを計算し
　　　　softmaxの値に従い重み付き加算を行う
　　　　これにより自分自身の他の場所の特徴に着目して自分自身を特徴づける

　　●　Position-Wise Feed-Forward Networks（全結合層）
　　　　位置情報を保持したまま順伝播させる
　　　　- 各Attention層の出力を決定
　　　 　- ２層の全結合NN
　　　 　- 線形変換→ReLu→線形変換
　　　 OUTPUTの次元を揃えている

　　●　Transformer-Encoder
　　　　自己注意機構により文脈を考慮して各単語をエンコード

　　●　Scaled dot product attention

　　　　全単語に関するAttentionをまとめて計算する
　　　　　$Attention(Q,K,V)=softmax \left ( \frac{QK^T} {\sqrt{d_k}} \right)V$
　　　　　Q,K,Vは元データは同じであるが、それぞれに線形変換されている

　　●　Multi-Head attention
　　　　重みパラメタの異なる８個のヘッドを使用
　　　　８個のScaled Dot-Product Attentionの出力をConcat
　　　　それぞれのヘッドが異なる種類の情報を収集

　　●　Decoder

　　　　・Encoderと同じく6層
　　　　　各層で二種類の注意機構
　　　　　注意機構の仕組みはEncoderとほぼ同じ
　　　　・自己注意機構
　　　　　生成単語列の情報を収集
　　　　　直下の層の出力へのアテンション
　　　　　未来の情報を見ないようにマスク
　　　　・Encoder-Decoder attention
　　　　　入力文の情報を収集
　　　　　Encoderの出力へのアテンション

　　●　Add & Normサブタイトル

　　　・Add (Residual Connection)
　　　　入出力の差分を学習させる
　　　　実装上は出力に入力をそのまま加算するだけ
　　　　効果：学習・テストエラーの低減
　　　・Norm (Layer Normalization)
　　　　各層においてバイアスを除く活性化関数への入力を平均０、分散１に正則化
　　　　効果：学習の高速化

　　●　Position Encoding

　　　・RNNを用いないので単語列の語順情報を追加する必要がある
　　　　単語の位置情報をエンコード
　　　　$PE_{pos,2i}=sin\left( \frac{pos}{10000^{2i/512}} \right)$
　　　　$PE_{pos,2i+1}=cos\left( \frac{pos}{10000^{2i/512}} \right)$

Section6)　物体検知・セグメンテーション

【物体検知】 　◆　広義の物体認識タスク  　◆　代表的データセット 　　●　様々なモデルの精度を比較するために共通のデータセットが必要 　　●　目的に応じた学習を行うためにどのような特性のデータセットを選択するか 　　　　データセットに対する知識が必要 　　下記いずれも物体検出コンペティションで用いられたデータセット 　　●　Box/画像が小さいければアイコン的な映りであり 　　　　日常感とはかけ離れやすい 　　●　Box/画像が大きければ部分的な重なり等も見られ 　　　　日常生活のコンテキストに近い 　　●　データセットは目的に応じたBox/画像の選択が必要 　　●　クラス数が大きいからといって良い訳ではない 　　 　◆　評価指標 　　●　Confusion Matrix  　　　　Precision = $\frac{TP}{TP+FP}$ 　　　　Recall = $\frac{TP}{TP+FN}$ 　　　※　confidenceの閾値を変化させるとこれらの値も変化する  　◆　IoU（Intersection over Union） 　　　物体検出においてはクラスラベルだけでなく 　　　物体位置の予測精度も評価したい  　　　・Ground-Truth BB に対する占有面積や、Predicted BB に対する占有面積で精度を測ることは 　　　　以下のような事がありえるのでNGである  　　●　入力１枚で見るPrecision/Recall  　　●　Precision/Recallの計算例（クラス単位）  　　●　AP（Average Precision） 　　　$AP=\int^1_0P(R)\;dR$（PR曲線の下側面積） 　　　※　クラスラベル固定のもとで考えていたことに注意 　　　　　（APはクラスごとに計算される）  　　●　mAP（mean Average Precision） 　　　クラス数が$C$なら 　　　$mAP=\frac{1}{C}\displaystyle\sum^C_{i=1} AP_i$

　　●　MS COCOで導入された指標
　　　IoU閾値は0.5で固定で計算していたがIoU閾値も変化させる
　　　
　　●　FPS（Flames per Second）
　　　物体検知応用上の要請から, 検出精度に加え検出速度も問題となる

　　　※　指標を出す際にどんなデータセットを使ったかも重要

　　●　物体検知のフレームワーク

　　●　SSD（Single Shot Detector）
　　　§　SSDとは
　　　　BBをあらかじめ適当な位置、大きさで用意する(Default Box 実際には複数用意されることが多い)
　　　　そしてSSDのネットワークを介し学習を進めることによってDefault Boxを修正していく

　　●　SSDのベースネットワークであるVGG16
　　　　16の所以は下記の「Convolition+ReLu」と「fully connected+ReLu」の数

　　●　SSDのネットワークアーキテクチャ
　　　・　青字の部分はSSDと異なっている点の説明
　　　・　紫色の文字の部分はSSDの特徴である解像度の異なる
　　　　　特徴マップから出力を作っていることの説明

　　●　特徴マップからの出力

　　　　　オフセット項：Default Boxのままでは物体の位置や大きさを正しく検出できているとは
　　　　　　　　　　　　限らないため中心位置や幅や高さを変更している

　　●　SSDのデフォルトボックス数
　　　　特徴マップからの出力で示したデフォルトボックスを
　　　　SSDのネットワークアーキテクチャの図に当てはめると下図のようになる
　　　　※　青字と赤字のDefault Boxの数の違いは計算上の都合によるもの

　　　・　上図のデフォルトボックス数の計算
　　　　　VOCデータセットではクラス数20に背景クラスが考慮され, #Class = 21となるので
　　　　　青字部分：4×(21+4)×38×38 + 4×(21+4)×3×3 + 4×(21+4)×1×1
　　　　　赤字部分：6×(21+4)×19×19 + 6×(21+4)×10×10 + 6×(21+4)×5×5
　　　　　合計　　：8,732×(21+4)

　　●　特徴マップの大きさ
　　　　特徴マップのサイズ変化を物理的な大きさを変えて描く慣習があるが実際には
　　　　変化しているのは解像度であり物理的な大きさではない
　　　　特徴マップの38×38などは解像度（ピクセル数）を表しており
　　　　　・　解像度が高い=ピクセル数が多いため小さな物体も検出できる
　　　　　・　解像度が低い=ピクセル数が少ないため全体に渡って映っているような
　　　　　　　物体でないと検出できない

　　●　多数のDefault Boxを用意したことで生ずる問題への対処
　　　・　Non-Maximum Suppression
　　　　　IoU同士の重なりが大きい場合は最もConfidence の大きなものを残し
　　　　　それ以外は排除する
　　　　　（IoU同士の重なりが小さい場合は
　　　　　　異なるものを検出している可能性があるので排除しない）
　　　・　Hard negative mining
　　　　　背景としてとらられるNegative Classの検出を抑える
　　　　　→　Positive ClassとNegative Classの比率を制限する

　　●　損失関数
　　　$L(x,c,l,g)=\frac{1}{N}(L_{conf}(x,c)+\alpha L_{loc}(x,l,g))$
　　　　$N$：正解ボックスとマッチしたデフォルトボックス数
　　　　（N=0の場合はloss値を0とする）
　　　　$l$：予想されたボックス
　　　　$g$：正解ボックス
　　　　$c$：バウンディングボックスの中心座標

　　　・　confidenceに対する損失
　　　　　$L_{conf}(x,c)=-\displaystyle\sum^N_{i∈Pos} x^p_{ij} log(\hat c^p_i) - \displaystyle\sum log(\hat c^0_i) ;;;where;;; \hat c^p_i= \frac{exp(c^p_i)}{\sum_p exp(c^p_i)}$

　　　・　検出位置に対する損失
　　　　　$L_{loc}(x,l,g)=\displaystyle\sum^N_{i∈Pos};;\displaystyle\sum_{m∈\{cx,cy,w,h\}};x^k_{ij}smooth_{L1}(l^m_i-\hat g^m_j)$

【Semantic Segmentation】
　　●　Up-sampling
　　　　Semantic Segmentationは入力画像と同じサイズの画像の各ピクセルに対して
　　　　クラス分類が行われる
　　　　→　畳み込みとプーリングによって解像度の落ちた状態に対して
　　　　　　Semantic Segmentationは行えない。なので
　　　　　落ちた解像度をどのようにして元の解像度に戻すのか(Up Sampling)が重要になる

　　　・　Poolingの必要性（解像度の落ちる原因のPoolingについて）
　　　　　小さなkernelのスライドを用いて画像を正しく認識するためには受容野に
　　　　　ある程度の大きさが必要
　　　　　受容野を広げる典型：①深いConv.層 ②プーリング（＆ストライド）
　　　　　①は多層化に伴う演算量・メモリの問題がある
　　　　　→　受容野の確保のためにPoolingを行う

　　●　fully convolution networt(FCN)
　　　　CNNでは畳み込み層と全結合層があるが、FCNはこの全結合層を畳み込み層に
　　　　置き換えたもの
　　　　全結合層を畳み込み層に置き換えることで、「物体がなにであるか」という出力から
　　　　「物体がどこにあるか」という出力になる

　　●　Deconvolution/Transposed convolution

　　　※　逆畳み込みと呼ばれることも多いが畳み込みの逆演算ではない
　　　　　→　当然, poolingで失われた情報が復元されるわけではない

　　●　輪郭情報の補完
　　　　pool5(1×1)より32倍にUpSamplingするのではなく、pool4(2×2)の情報をpool5に渡し
　　　　2×2にUpSamplingしたpool5と、pool4(2×2)を要素ごとに足し算
　　　　（element-wise addition）した上で、4×4にUpSamplingする
　　　　さらにこれ↑とpool3(4×4)の情報を足したのち、32×32にUpSamplingする

　　●　U-Net
　　　・　FCNとの違い
　　　　　Up-samplingした後の低レイヤー情報との結合方法が異なる
　　　　　　FCN：Up-samplingしたものと低レイヤー情報とを要素ごと（element-wise）に
　　　　　　　　　足し算
　　　　　　U-Net：Up-samplingしたものと低レイヤー情報とをチャネル方向に結合

　　●　Unpooling
　　　pooling時に元の位置情報を記憶しておき、戻すときにはこれをもとにUnpoolingを行う
　　　Up-sampling方法

　　●　Dilated Convolution
　　　Convolutionの段階で受容野を広げる工夫
　　　Kernel（ここでは3×3）の間に隙間を用いてカバーできる範囲を広げながら
　　　計算量はもとの（3×3）のままである

　　　3×3のKernelのまま畳み込むと、
　　　15×15 → 13×13 → 11×11 → 9×9 → 7×7 → 5×5 → 3×3 → 1×1と
　　　７層のConvolution層が必要になる

実装演習

　◆　4_1_tensorflow_codes_after 　　●　線形回帰 　　・　noiseを変更 　　　　noiseが大きすぎると誤差も大きくなった  　　・　dを変更 　　　　誤差についてnoiseのような分かりやすい差は発生しなかった 　　　　それぞれ何度か試したが下図に表れている誤差の違いは 　　　　試行結果の振り幅の範囲内のようであった  　　●　非線形回帰 　　・　noiseを変更 　　　　noiseの大小が誤差の大小と一致している  　　・　dを変更 　　　　(1) 小さくする 　　　　　　xの３つの係数の値を小さくして試行してみた結果グラフの形は変わるが 　　　　　　誤差にあまり変化は見られなかった 　　　　(2) 大きくする 　　　　　　xの３つの係数の値を大きくして試行してみた結果グラフの形も変わったが 　　　　　　誤差が大きくなった

　　・　次の式をモデルとして回帰を行おうy=30x2+0.5x+0.2
　　　　左がそのまま実行した結果
　　　　右が試行錯誤した後の結果
　　　　誤差が収束しないのは学習率が高いのかと考え、0.0001まで下げ、
　　　　100万回回してみたが完全には収束せず、時間が非常にかかったため、
　　　　時間と収束具合のバランスの調整を試みた結論が右側
　　　　どの状態をもって収束とみなすかは非常に判断が難しい

　　●　分類1層
　　　　iters_numの回数を増やし、オプティマイザをadamにして試行すると正解率が
　　　　改善された

　　●　分類3層
　　　・　隠れ層を減らすと正解率は下がり、増やすと正解率は上がった

　　　・　オプティマイザは一般的にはがAdamが良いとされているが
　　　　　今回のデータに限ってはPMSPropが学習スピード、正解率ともに
　　　　　良い結果であった
　　　　　しかし各オプティマイザの学習率を変更すれば結果は変わるかもしれない

　　●　分類CNN
　　　・　keep_prob:1.0(ドロップアウトなし)、keep_prob:0.5(半分ドロップアウト)を
　　　　　試してみたがドロップアウトの効果は得られなかった。
　　　　　keep_prob:0.9～0.6の間も試したが、0.7あたりから少しずつ
　　　　　正解率が落ちていってしまった

◆　4_3_keras_codes_after
　●　分類 (iris)
　　・　SGDはReLu,Sigmoidいずれの場合も有効でなさそうであった

　●　分類 (mnist)
　　・　Ir(学習率)を0.01に変更するとtrainデータの正答率より
　　　　testデータの正答率が良くなるという珍しい結果になった
　　・　decay(学習率減衰)を0.001に変更するとtrainデータの正答率は良くなったが
　　　　testデータの正答率は比例して良くはならなかった

　●　RNN
　　　指定してある変更を全て行って実行すると正答率が非常に悪くなったので
　　　dropoutだけ無くしてみたところ正答率が変更前の実行結果よりも良くなった

◆　lecture_chap1_exercise_public、lecture_chap2_exercise_public
　●　Attentionを使用していない上段の結果は10回のepochで、valid_lossやvalid_blueの値に
　　　改善が望めなさそうになっている
　●　Attentionを使用している下段の結果は10回のepochで、上段の精度を上回っており
　　　さらにepochが15回の時点でまだ精度に改善の余地がありそうに思える
　●　文章の生成においてもAttentionなしの方では、意味の通じない文章が作成される
　　ことが多かったが、Atenttionありの方では意味の通る文章が作成されることが
　　多くなった