機械学習
$\huge{回帰問題}$ ある入力(離散あるいは連続値)から出力(連続値)を予測する問題線形回帰モデル
§ 線形回帰モデルとは ● 回帰問題を解くための機械学習モデルの1つ ● 「教師あり学習の回帰手法」の1つ ● 目的変数が説明変数の係数に対して線形(直線)なモデルを学習するもの ● 訓練データに適合する回帰係数を学習する際、二乗誤差の最小化を行う。 ● 入力とm次元パラメータの線形結合(※1)を出力するモデル ※1 線形結合 ・ 入力ベクトルと未知のパラメータの各要素を掛け算し足し合わせたもの ・ 入力ベクトルとの線形結合に加え、切片も足し合わせる ・ 出力は1次元(スカラ)となる§ 線形回帰の特徴 ● 外れ値に敏感である ● 説明変数間に相関があると,良い推定ができない可能性がある ● モデルの表現力を下げた方がよい場合もある ● 訓練データが多いほど過学習が起きやすく、 訓練データが少ないと学習不足が起きやすい
◆ 回帰で扱うデータ 〇 入力(説明変数または特徴量)・・・m次元のベクトル 〇 出力(目的変数)・・・スカラー値 〇 説明変数と目的変数の相関係数は-1~1まで値をとり -1に近いほど負の相関関係が強く、 1に近いほど正の相関関係が強い。 また0に近い場合は相関関係が弱い。
◆ モデルのパラメータ 〇 モデルに含まれる推定すべき未知のパラメータ 〇 特徴量が予測値に対してどのように影響を与えるをか決定する重みの集合 ・ 正の(負の)重みをつける場合、その特徴量の値を増加させると、 予測の値が増加(減少) ・ 重みが大きければ(0であれば)、その特徴量は予測に大きな影響力を持つ (全く影響しない) 〇 切片 ・ y軸との交点を表す
$\hat{y} = w^Tx + w_o = \displaystyle\sum_{j=1}^mw_jx_j+w_0$
※ $\hat{y}は予測値、x(x_j)は説明変数、w^T(w_j)は重み(回帰係数)、w_0は切片$
◆ 単回帰モデル
・ 説明変数が1次元
・ 直線
・ データは回帰直線に誤差が加わり観測されていると仮定
モデル数式
$y = w_o + w_1x_1 + ε$
※ $y$:目的変数 → 入力データ
$w_0$:切片 → 学習で決める
$w_1$:回帰係数 → 学習で決める
$x_1$:説明変数 → 入力データ
$ε$:誤差
複数の入力データ($x_1とy_1、x_2とy_2、・・・x_nとy_n$)より
以下のような連立方程式が立てられる
$y_1 = w0 + w_1x_1 +ε_1$
$y_2 = w0 + w_1x_2 +ε_2$
$\vdots$
$y_n = w0 + w_1x_n +ε_n$
これを行列で表現すると
$y=Xw+ε$ となる
◆ 線形重回帰モデル
・ 説明変数が多次元
・ 曲面
・ データは回帰曲面に誤差が加わり観測されていると仮定
モデル数式
$y = w_o + w_1x_1 + w_2x_2 + ε$
※ $y$:目的変数 → 入力データ
$w_0$:切片 → 学習で決める
$w_1,w_2$:回帰係数 → 学習で決める
$x_1,x_2$:説明変数 → 入力データ
$ε$:誤差
複数の入力データ($x_{11},x_{12},…x_{1m}とy_1、x_{21},x_{22},…x_{2m}とy_2、$
$… x_{n1},x_{n2},…x_{nm}とy_n$)より以下のような連立方程式が立てられる
$y_1 = w0 + w_1x_{11} + w_2x_{12} + … + w_mx_{1m} + ε_1\\ y_2 = w0 + w_1x_{21} + w_2x_{22} + … + w_mx_{2m} + ε_2\\ \vdots\\ y_n = w0 + w_1x_{n1} + w_2x_{n2} + … + w_mx_{nm} + ε_n$
これを行列で表現すると $y=Xw+ε$ となる ◆ (モデルに入力する)データの分割
学習用データ:機械学習モデルの学習に利用するデータ
検証用データ:学習済みモデルの精度を検証するためのデータ
〇 分割する理由
・ モデルの汎化性能を測定するため
・ データへの当てはまりの良さではなく、未知のデータに対して
どれくらい精度が高いかを測りたい
◆ パラメータの推定
平均二乗誤差($MSE$=Mean Squared Error)を用いて推定する
$MSE = \displaystyle\frac{1}{n} \sum_{i=0}^{n-1} (\hat{y_i} – y_i)^{2}$
( $\hat{y_i}$:予測値、 $y_i$:実際の値、 $n$:データの総数 )
実際の値と予測値の絶対値の 2 乗の平均を最小にすることでパラメータを推定する
※ 実際の計算
$MSE$を最小にするにはその勾配が0になる点を求める
→ $MSE$を$w$に関して微分したものが0となる$w$の点を求める
$\frac{\partial}{\partial w} MSE=0$
$⇒\frac{\partial}{\partial w}\{{\frac{1}{n}\displaystyle\sum^n_i (\hat{y_i}-y_i)^2}\}=0$
($\hat{y_i}(予測値)=Xw$)
$⇒\frac{1}{n}\frac{\partial}{\partial w}\{(Xw-y)^T(Xw-y)\}=0$
($片方を転置して(Xw-y)を2乗にしている$)
$⇒\frac{1}{n}\frac{\partial}{\partial w}\{(w^TX^T-y^T)(Xw-y)\}=0$
$⇒\frac{1}{n}\frac{\partial}{\partial w}\{w^TX^TXw-w^TX^Ty-y^TXw +y^Ty\}=0$
$⇒\frac{1}{n}\frac{\partial}{\partial w}\{w^TX^TXw-2w^TX^Ty+y^Ty\}=0$
($w^TX^Ty$ と $y^TXw$ は実質的に同じなのでまとめて $2w^TX^Ty$ としている)
★ ここでベクトルの微分について公式
$\frac{\partial}{\partial w}w^TAw = (A+A^T)w$
$\frac{\partial}{\partial w}w^TA = A$
より
$⇒\frac{1}{n}\{X^TX+(X^TX)^T\}w-2X^Ty=0 $
$⇒2X^TXw-2X^Ty=0 $
$⇒X^TXw-X^Ty=0$
$⇒X^TXw=X^Ty$
$⇒(X^TX)^{-1}(X^TX)w=(X^TX)^{-1}X^Ty$
$⇒\hat{w}=(X^TX)^{-1}X^Ty ← 回帰係数$
求めた回帰係数より
【予測値】
$\hat{y}=X(X^TX)^{-1}X^Ty$
線形回帰モデル 実装演習
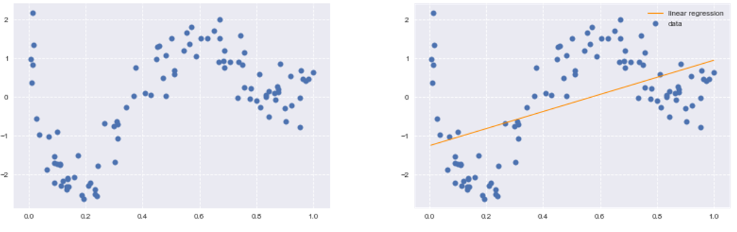
Boston Hausing Data を sklean でなく numpyで 線形回帰してみる (1) 単回帰 ・ 説明変数 RM(ルーム数) ※ 考察 ・回帰係数、切片とも、sklearnもnumpyも同じ数値となっており、 numpyで正しく実装できていると思われる ・最終出力の回帰直線のグラフはそれらしい線になっているが外れ値が多いので その影響を受けていると考えられる  (2) 重回帰 ・ 説明変数 CRIM(犯罪率)、RM(ルーム数) ※ 考察 ・回帰係数、切片、予測値ともsklearnもnumpyも同じ数値となっており、 numpyで正しく実装できていると思われる ・5件目までではあるが説明変数(CRIM,RM)とそれによる予測値を見ると CRIMよりもRMの方が住宅価格への影響が大きいように思われる 非線形回帰モデル
§ 線形回帰モデルとは ● (同) 回帰問題を解くための機械学習モデルの1つ ● (同)「教師あり学習の回帰手法」の1つ ● (異) 目的変数が説明変数の係数に対して非線形(曲線)なモデルを学習するもの ● (同) 訓練データに適合する回帰係数を学習する際、二乗誤差の最小化を行う ※ (同)は線形回帰と同じ、(異)と異なる部分 ◆ 複雑な非線形構造を内在する現象に対して、非線形回帰モデリングを実施
〇 データの構造を線形で捉えられる場合は限られる
〇 非線形な構造を捉えられる仕組みが必要
↓ このような分布のデータに対して線形回帰ではデータの構造を捉えられない
◆ 基底展開法
〇 回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの
線型結合を使用
〇 未知パラメータは線形回帰モデルと同様に最小2乗法や最尤法により推定
$y_i = f(x_i)+ε_i$
$y_i = w_0+\displaystyle\sum^m_{j=1}w_j\phi_j(x_i)+ε_i$
◆ よく使われる基底関数
〇 多項式関数
〇 ガウス型基底関数
〇 スプライン関数/ Bスプライン関数
◆ 式
・ 説明変数
$x_i = (x_{i1},x_{i2},・・・,x_{im})∈\mathbb{R}^m m$:説明変数の数
・ 非線形関数ベクトル
$\phi(x_i)=(\phi_1(x_i),\phi_2(x_i),・・・\phi_k(x_i))^T∈\mathbb{R}^k k$:既定関数の数
・ 非線形関数の計画行列
$\Phi=(\phi(x_1),\phi(x_2),・・・\phi(x_n))^T∈\mathbb{R}^{n×k}$
・ 最尤法による予測値
$\hat{y}=\Phi(\Phi^T\Phi)^{-1}\Phi^Ty$
線形モデルの予測値$\hat{y}$は
$\hat{y}=X(X^TX)^{-1}X^Ty$ なので、基底展開法も線形回帰と同じ枠組みで推定可能
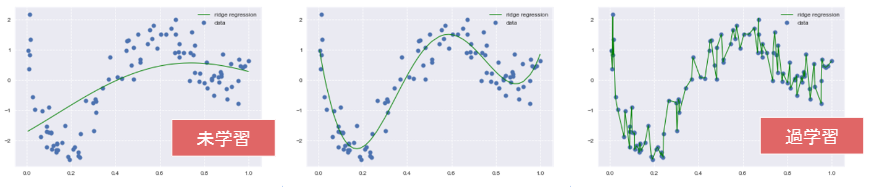
◆ 未学習と過学習
〇 未学習
・ 学習データに対して、十分小さな誤差が得られないモデル
⇒ (対策) モデルの表現力が低いため、表現力の高いモデルを利用する
〇 過学習
・ 小さな誤差は得られたけど、テスト集合誤差との差が大きいモデル
⇒ (対策1) 学習データの数を増やす
(あまりに膨大な数はデータの収集が困難かつ計算コストが大)
(対策2) 不要な基底関数(変数)を削除して表現力を抑止
(特徴量、既定関数の選択にはドメイン知識が必要、
取捨選択の難しさがある
ドメイン知識に頼らず純粋に統計的な方法として
赤池情報量規準を用いる手法もある)
(対策3) 正則化法を利用して表現力を抑止
(ドメイン知識に関係なく用いることができる)
↓ 真ん中のモデルのようにしたい
◆ 過学習の対策
〇 不要な基底関数を削除
・ 基底関数の数、位置やバンド幅によりモデルの複雑さが変化
・ 解きたい問題に対して多くの基底関数を用意してしまうと
過学習の問題がおこるため、
適切な基底関数を用意(CVなどで選択)
〇 正則化法(罰則化法)
・「モデルの複雑さに伴って、その値が大きくなる正則化項(罰則項)を
課した関数」を最小化
・ 正則化項(罰則項)
形状によっていくつもの種類があり、それぞれ推定量の性質が異なる
・ 正則化(平滑化)パラメータ
モデルの曲線のなめらかさを調節→適切に決める必要あり
$MSE$を変形し以下の$S_\gamma$を最小とするような$w$を求める
$S_\gamma=(y-$$\Phi$$w)^T(y-\Phi w)+\gamma R(w) \gamma(>0)$
※ 既定関数の数(k)が増加するとパラメータが増加し、
残差は減少(モデルが複雑化)
※ $\gamma R(w)$はモデルの複雑さに伴う罰則
過学習のときは回帰係数の値が大きくなりがちなので、
$\gamma R(w)$も含めた最小値を求める事で回帰係数の大きくなりすぎを防いでいる
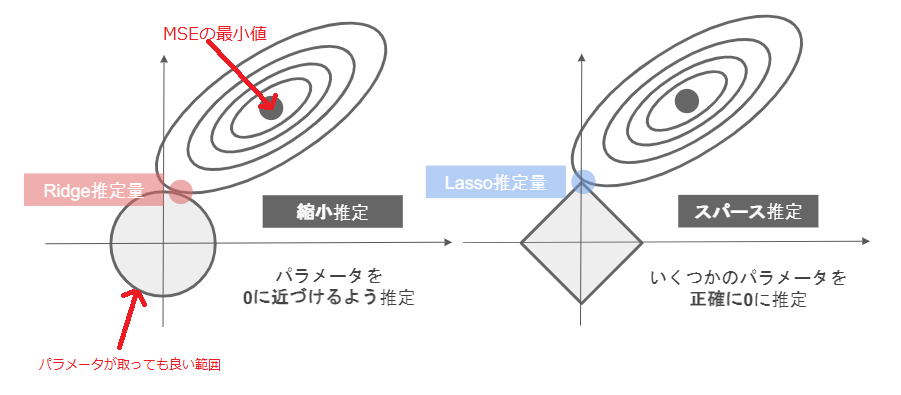
〇 正則化項(罰則項)($R(w)$)の役割
・ 無い → 最小2乗推定量
・ L2ノルムを利用 → Ridge推定量
・ L1ノルムを利用 → Lasso推定量
〇 正則化パラータ($\gamma$)の役割
・ 小さく → 制約面(回帰係数(=パラメータ)が取ってもよい範囲)が大きく
・ 大きく → 制約面が小さく
◆ モデルの汎化性能測定
§ 汎化性能
〇 学習に使用した入力だけでなく
これまで見たことのない新たな入力に対する予測性能
・ 検証誤差が小さいものが良い性能を持ったモデル
・ 検証誤差は通常、学習データとは別に収集された検証データでの
性能を測ることで推定
〇 バイアス・バリアンス分解
・ 検証誤差の期待値をバイアス+バリアンス+ノイズの
3つの和に分解すること
【学習誤差】
$MSE_{train}=\frac{1}{n_{train}}\displaystyle\sum^{n_{train}}_{i=1}(\hat{yi}^{(train)}-y_i^{(train)})^2$
【検証誤差】
$MSE_{test}=\frac{1}{n_{test}}\displaystyle\sum^{n_{test}}_{i=1}(\hat{yi}^{(test)}-y_i^{(test)})^2$
◆ 未学習/過学習の判断
・ 訓練誤差もテスト誤差も小さい → 汎化しているモデルの可能性
・ 訓練誤差は小さいがテスト誤差が大きい → 過学習
・ 訓練誤差もテスト誤差も小さくならない → 未学習
(表現力が足らないモデルで起きる)
◆ ホールドアウト法
〇 有限のデータを学習用と検証用の2つに分割し、
「予測精度」や「誤り率」を推定する為に使用
・ 学習用を多くすれば検証用が減り学習精度は良くなるが
性能評価の精度は悪くなる
・ 検証用を多くすれば学習用が減少するので
学習そのものの精度が悪くなる
・ 手元にデータが大量にある場合を除いて
良い性能評価を与えないという欠点がある
・ 外れ値が検証データに入った場合、外れ値に当てはまりが良い
モデルの性能が高く評価されてしまう
〇 基底展開法に基づく非線形回帰モデルでは、
基底関数の数、位置、バンド幅の値とチューニングパラメータを
ホールドアウト値を小さくするモデルで決定する非線形回帰モデル
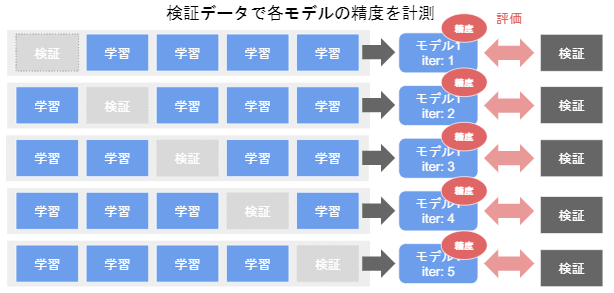
◆ クロスバリデーション(交差検証)
全データを3分割以上の任意の数に分割し、1つを検証用、残りを学習用として
学習、検証を行ったのち、先ほどと異なる検証用データ、残りを学習用データとして
学習、検証を行い、分割したデータ全てが1回ずつ検証用データとして使用される。
・ クロスバリデーションはデータが少ないときによく使われる
・ 汎化性が高いことがメリットとして上げられる
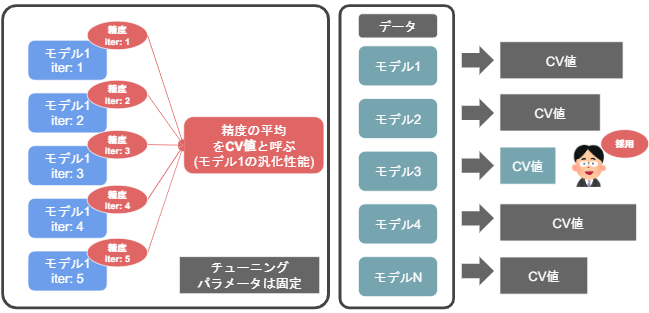
〇 モデルの選び方
モデルごとに検証結果の精度を平均し、その平均値(CV値)の
最も優れたモデルを選ぶ
◆ グリッドサーチ
〇 全てのチューニングパラメータ(ハイパーパラメータ)の組み合わせで
評価値を算出
〇 最も良い評価値を持つチューニングパラメータを持つ組み合わせを
「いいモデルのパラメータ」として採用
非線形回帰モデル 実装演習
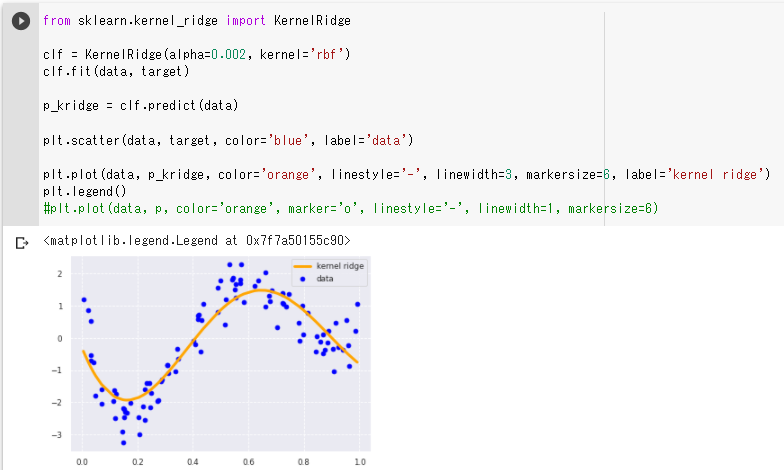
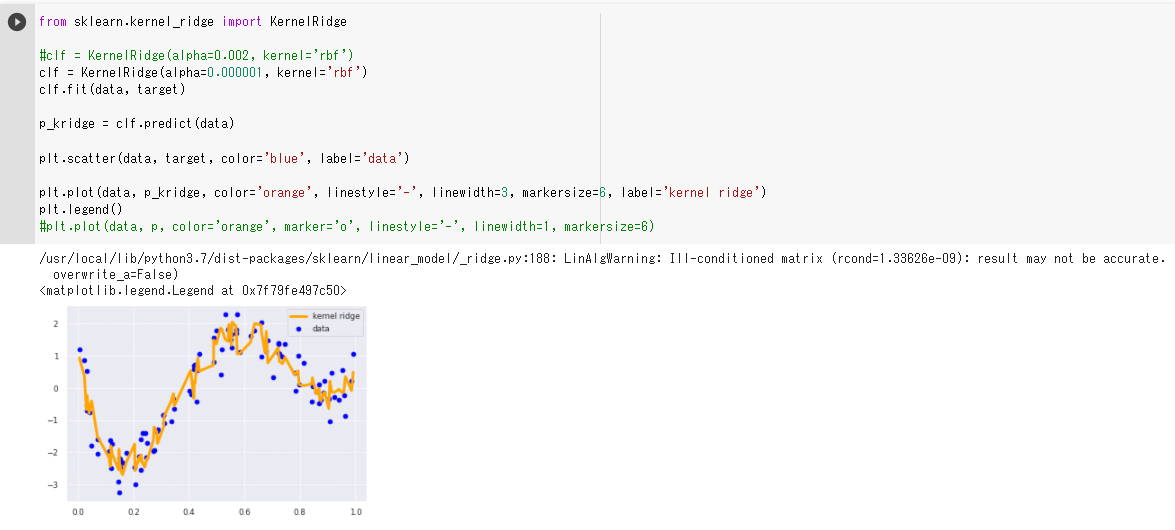
(1)非線形のデータを線形回帰で予測 ・ まったく予測になっていない  (2)非線形のデータをカーネルリッジ回帰を使って予測
・ 左右の上昇部分を捉えられていないように見えるので、正則化項の値を小さくしてみる
・ 正則化項の値を小さくすると左右の上昇部分も捉えられるようになった
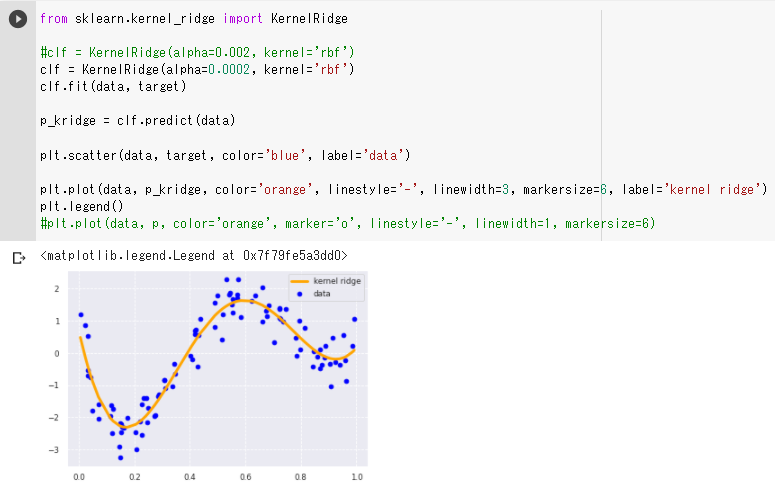
・ 正則化項の値を小さくしすぎると正則化が効かず過学習を起こしていると思われる
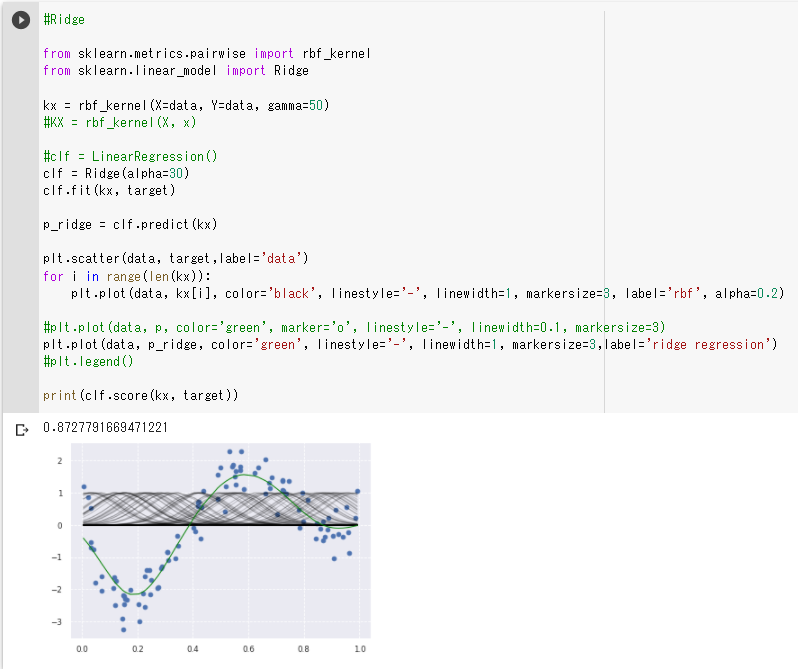
(3)非線形のデータをrbf_kernelとリッジ回帰を使って予測
・ 左右の上昇部分の捉え方が弱いように見えるので(2)と同じように正則化項の値を小さくしてみる
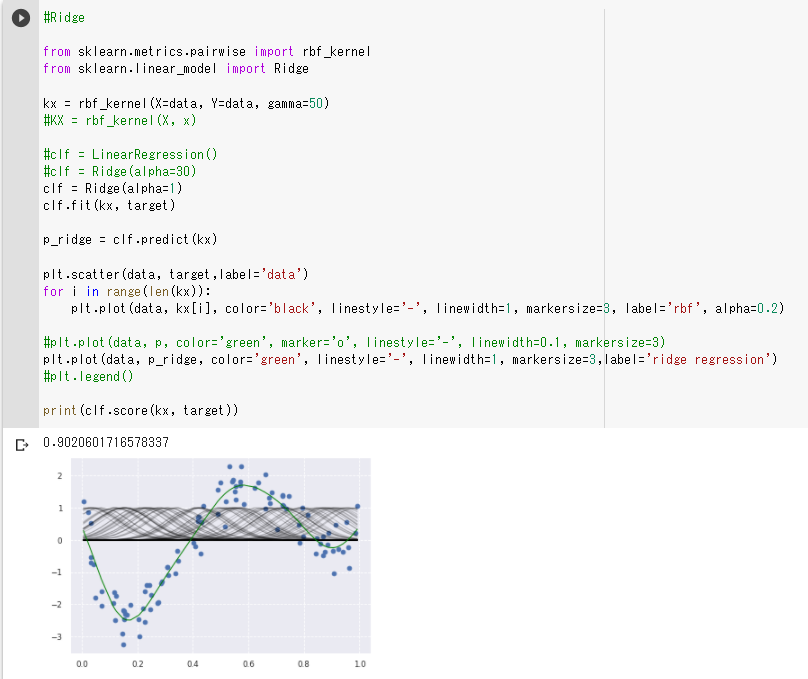
・ 正則化項の値を小さくすると左右の上昇部分も先ほどよりしっかり捉えられるようになった
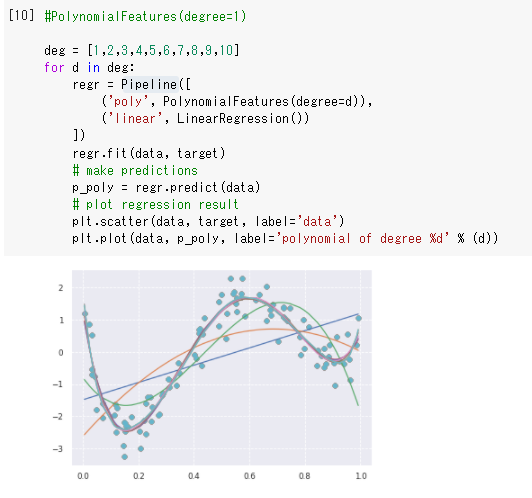
(4)非線形のデータを多項式回帰を使って予測
・4次元目以降の線は殆ど違いが無いように見えるので5次元より後は要らないように思う
(5)非線形のデータをrbf_kernelとラッソ回帰を使って予測
・予測が線形になってしまったのは正則化項が大きすぎるからではないか
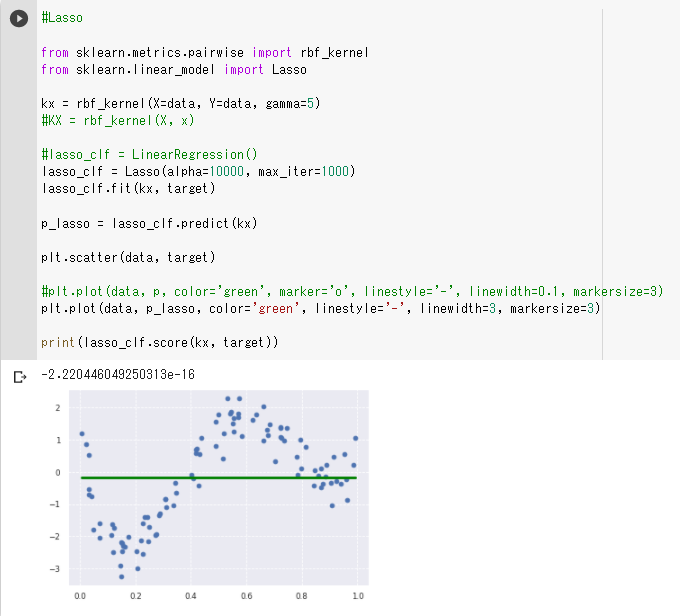
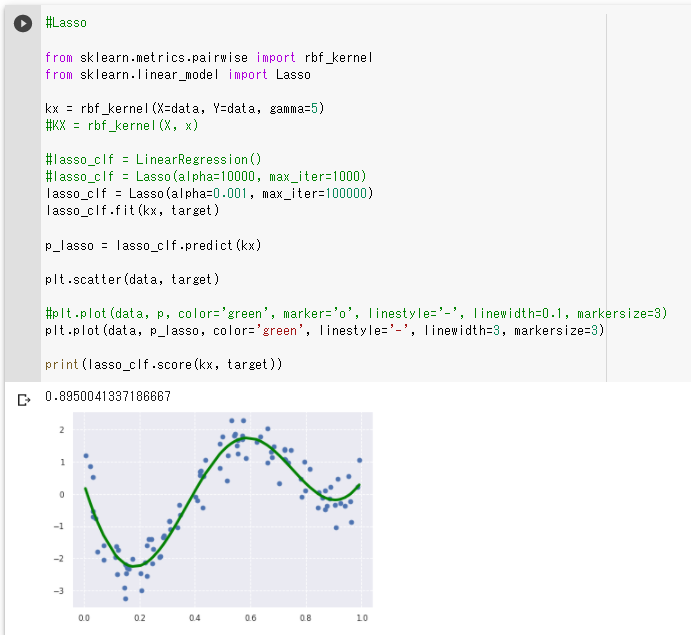
・正則化項を小さくするとモデルの精度が良くなった
また、ConvergenceWarning: Objective did not converge.
と出るようになったので、出なくなるまで反復回数を増やした
(反復回数はモデルの制度にそれほど影響はなかった)
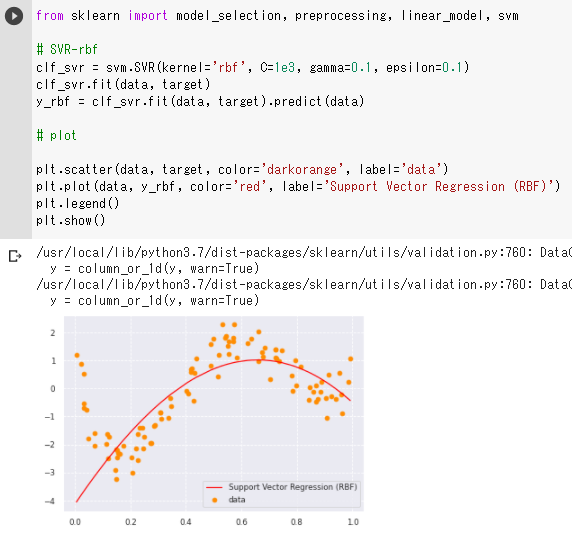
(6)非線形のデータをサポートベクター回帰を使って予測
・ 正則化パラメータの値(C=1e3)が小さくて正則化が強く効きすぎているのではないかと
予想する
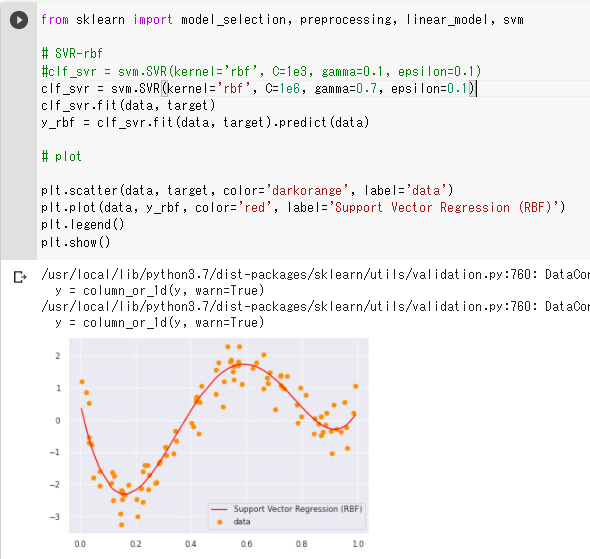
・正則化パラメータの値を大きくし(C=1e6)、カーネル係数の値も大きくすると
(gamma=0.7)モデルの精度が良くなった
(誤差の不感帯=epsilonの値はよほど大きくしない限り影響は見られなかった)
(7)ニューラルネットワークによる予測
・最初に記載されていたmodel.addの数を減らして層を少なくすると
モデルの精度が下がった
・最初に記載されていたmodel.addより数を増やして層を多くしても
モデルの精度はあまり変化がなかった
ロジスティック回帰
§ ロジスティック回帰とは ●「教師あり学習の分類手法」の1つ ● 2値分類では入力が一方のクラスに属する確率を出力するように学習する ● ロジスティック回帰では学習の際,尤度関数の最大化を行う。 § ロジスティック回帰の特徴 ● 主に2値分類に使われるアルゴリズム ● 線形の決定境界で分離できない場合、非線形な決定境界を探す 高次の特徴空間へ写像する,新たな特徴量にしてから適用するなどの工夫が必要 ● 識別的アプローチ(※1)に属する ※1 識別的アプローチ $x$が与えられたときのクラス$C_k$に割り当てられる確率$p(C_k|x)$を直接モデル化 これに対して生成的アプローチとは $p(C_k)とp(x|C_k)$をモデル化しその後ベイズの定理を用いて$p(C_k|x)$を求める $p(C_k|x)=\frac{p(C_k,x)}{p(x)}=\frac{p(x|C_k)p(C_k)}{p(x)}$ 外れ値の検出ができる、GANのような新たなデータ生成ができる◆ ロジスティック回帰モデルの式
入力とm次元パラメータの線形結合をシグモイド関数に入力
出力はy=1になる確率の値になる
$\sigma(\displaystyle\sum^m_{j=1}w_jx_j+w0) ※\sigmaはシグモイド関数$
〇 パラメータ
$w=(w_1,w_2・・・w_m)^T∈\mathbb{R}^{m}$
〇 シグモイド関数
$\sigma(x)=\frac{1}{1+exp^{-ax+b}}$
・ 入力は実数・出力は必ず0~1の値
・ (クラス1に分類される)確率を表現
・ 単調増加関数
・ aを増加させると,x=0付近での曲線の勾配が増加
・ aを極めて大きくすると,単位ステップ関数
(x<0でf(x)=0,x>0でf(x)=1となるような関数)に近づく
・ b(バイアス)の変化は段差の位置が変化
bを大きくすると段差は右にずれる

・ シグモイド関数の微分
$\frac{\partial \sigma(x)}{\partial x}=\frac{\partial}{\partial x}(\frac{1}{1+exp^{-ax+b}})=a\sigma(x)(1-\sigma(x))$
◆ 回帰係数の決定方法
〇 同時確率
・ あるデータが得られた時、それが同時に得られる確率
・ 確率変数は独立であることを仮定すると、それぞれの確率の掛け算となる
〇 尤度関数
・ データは固定し、パラメータを変化させる
・ 尤度関数を最大化するようなパラメータを選ぶ推定方法を最尤推定という
【1回の試行で$y=y_z$になる確率】
$P(y)=p^y(1-p)^{1-y}$
【n回の試行で$y_1~y_n$が同時に起こる確率($p$固定)】
$P(y_1,y_2,・・・y_n;p)=\displaystyle\prod_{i=1}^{n}p^{yi}(1-p)^{1-y_i}・・・pは既知、P(y)を求めている$
【$y_1~y_n$のデータが得られた際の尤度関数】
$P(y_1,y_2,・・・y_n;p)=\displaystyle\prod_{i=1}^{n}p^{yi}(1-p)^{1-y_i}・・・P(y)は既知、pを求めたい$
〇 最尤推定
・ 確率pはシグモイド関数となるため、推定するパラメータは重みパラメータ
・ $(x_1,y_1),(x_2,y_2),・・・(x_n,y_n)$を生成するに至った尤もらしい
パラメータ($w$)を探す
$P(Y=y_1|x_1)=p^{y_1}_1(1-p_1)^{1-y_1}=\sigma(w^Tx_1)^{y_1}(1-\sigma(w^Tx_1))^{1-y_1}$
$P(Y=y_2|x_2)=p^{y_2}_2(1-p_2)^{1-y_2}=\sigma(w^Tx_2)^{y_2}(1-\sigma(w^Tx_2))^{1-y_2}$
$\vdots$
$P(Y=y_n|x_n)=p^{y_n}_n(1-p_n)^{1-y_n}=\sigma(w^Tx_n)^{y_n}(1-\sigma(w^Tx_n))^{1-y_n}$
1~nまでの$w$を含んだ計算式をまとめると
$L(w)=\displaystyle\prod_{i=1}^{n}\sigma(w^Tx_i)^{y_i}(1-\sigma(w^Tx_i))^{1-y}$
〇 尤度関数を最大化するパラメータ($w$)を探す
■ 対数をとる
理由
・ 尤度は確率の掛算なので多くの確率を掛けていくと桁落ちするのでそれを防ぐ
・ 同時確率の積が和に変換できる
・ 指数が積の演算に変換できる
・ 対数をとっても最大になる点は変わらない
・ 「尤度関数にマイナスをかけたものを最小化」し「最小2乗法の最小化」と
合わせる
上記$L(w)$の対数をとると
$E(w)=-logL(w)=-\displaystyle\sum^n_{i=1}\{{y_ilog(p_i)+(1-y_i)log(1-p_i)\}}$
■ 勾配降下法で探す
シグモイド関数を含むため解を1度の微分で求めることはできないため
反復学習によりパラメータを逐次的に更新する
$w^{(k+1)}=w^{(k)}-\eta\frac{\partial E(w)}{\partial w} ・・・①$
※ $\eta$は学習率でハイパーパラメータ
(実際の計算方法)
$-\displaystyle\sum^n_{i=1}\{{y_ilog(p_i)+(1-y_i)log(1-p_i)\}}$
$(p_i=\sigma(w^Tx_i)=\frac{1}{exp^{(w^Tx_i)}}、z=w^Tx_iと置く)$
$\frac{\partial E(w)}{\partial w}=-\displaystyle\sum^n_{i=1}\frac{\partial E_i}{\partial p_i}×\frac{\partial p_i}{\partial z_i}×\frac{\partial z_i}{\partial w}$
$=-\displaystyle\sum^n_{i=1}\left(\frac{y_i}{p_i}-\frac{1-y_i}{1-p_i}\right)×p_i(1-p_i)×x_i$
$=-\displaystyle\sum^n_{i=1}\{{y_i(1-p_i)-(1-y_i)p_i\}}x_i$
$=-\displaystyle\sum^n_{i=1}(y_i-p_i)x_i$
①式に代入して
$w^{(k+1)}=w^{(k)}+\eta\displaystyle\sum^n_{i=1}(y_i-p_i)x_i ・・・②$
パラメータが更新されなくなるまで②式を繰り返す
■ データ件数が多い場合は確率的勾配降下法を利用する
nが巨大になった時にデータをオンメモリに載せる容量が足りない、
計算時間が莫大になるなどの問題を解決
§ 確率的勾配降下法(SGD)
・ データを一つずつランダムに(「確率的」に)選んでパラメータを更新
・ 勾配降下法でパラメータを1回更新するのと同じ計算量でパラメータを
n回更新できるので効率よく最適な解を探索可能
$w^{(k+1)}=w^{(k)}+\eta(y_i-p_i)x_i$
■ 分類の評価方法
〇 正解率がよく使われる
$\frac{TP+TN}{TP+FN+FP+TN}$
$※ TP:TruePositive TN:TrueNegative、$
$FN:FalseNegative、FP:FalsePositive$
〇 再現率(Recall)
・「本当にPositiveなもの」の中からPositiveと予測できる割合
(NegativeなものをPositiveとしてしまう事象については考えていない)
(Positiveを見逃しが多くないかが分かる)
・「えん罪(False Positive)が多少多くても、見逃し(False Negative)は避けたい」際に利用
$\frac{TP}{TP+FN}$
〇 適合率(Precision)
・ モデルが「Positiveと予測」したものの中で本当にPositiveである割合
(本当にPositiveなものをNegativeとしてしまうことについては考えていない)
(間違えてPositiveとした(False Positive)ものが多いか少ないかがわかる)
・ 見逃し(False Negative)が多くても、えん罪(False Positive)は避けたい」際に利用
$\frac{TP}{TP+FP}$
〇 F値
・ 理想的にはどちらも高いモデルがいいモデルだが、
両者はトレードオフの関係にあり、
どちらかを小さくすると、もう片方の値が大きくなってしまう
・ 適合率と再現率の調和平均
$\frac{2×適合率×再現率 }{ 適合率+再現率 }$
ロジスティック回帰 実装演習
(1) 1変数でのロジスティック回帰 ・チケット価格が高い方が生存率が高く、 チケット価格が安い方が生存率が低い。  (2) 2変数でのロジスティック回帰 ・年齢は生存率とあまり関係ないように見える ・(乗客の社会階級+性別)については、 乗客の社会階級は高いほうが生存率が高いように見えるが これはチケット価格とも結びついているように思える。 男女についてはこの結果からはどちらとも判断できない。  (3) クロスバリデーションでの実行とモデル評価
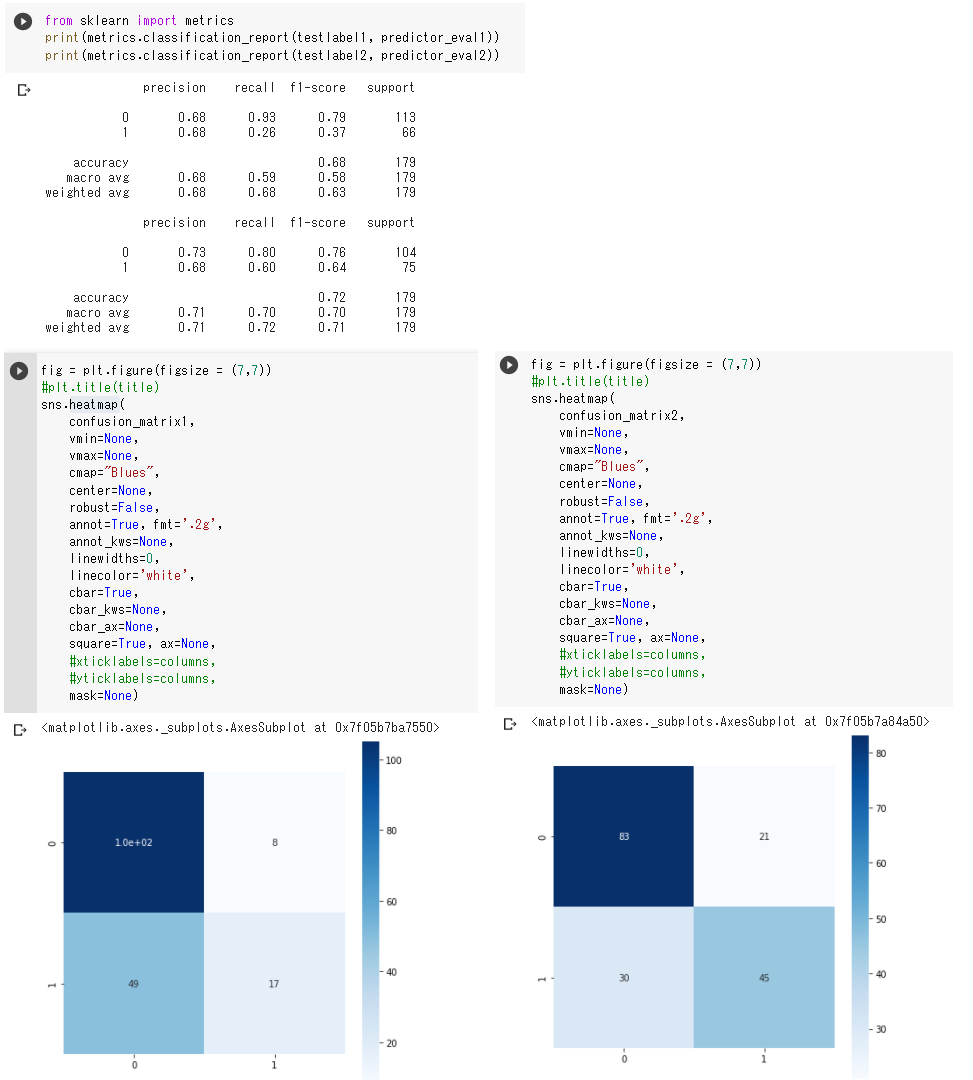
・変数1つと変数2つでのロジスティック回帰の結果、適合率はどちらも悪くないが
変数1の方は生存の再現率の値が低い。
変数1の生存はF値も低く、全体的に変数2つでの回帰の方がモデルとして良いと思われる。
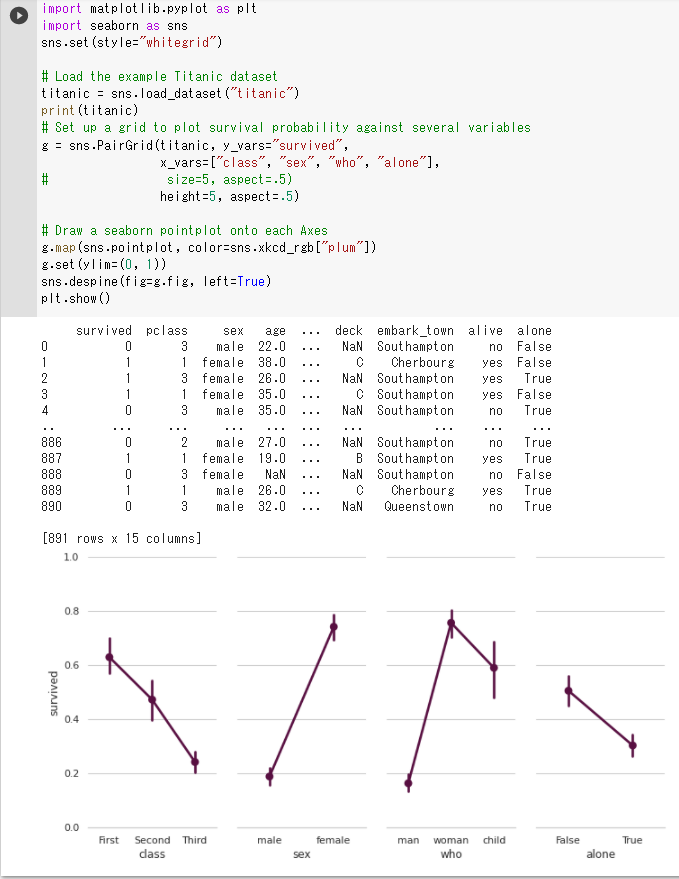
(4) seabornを使ってデータを見る1
・クラス
First→Second→Thirdと生存率が下がっている
・性別
女性の生存率が高い
・男/女/子供
男性の生存率が最も低い
・一人かどうか
一人の場合の生存率が低い
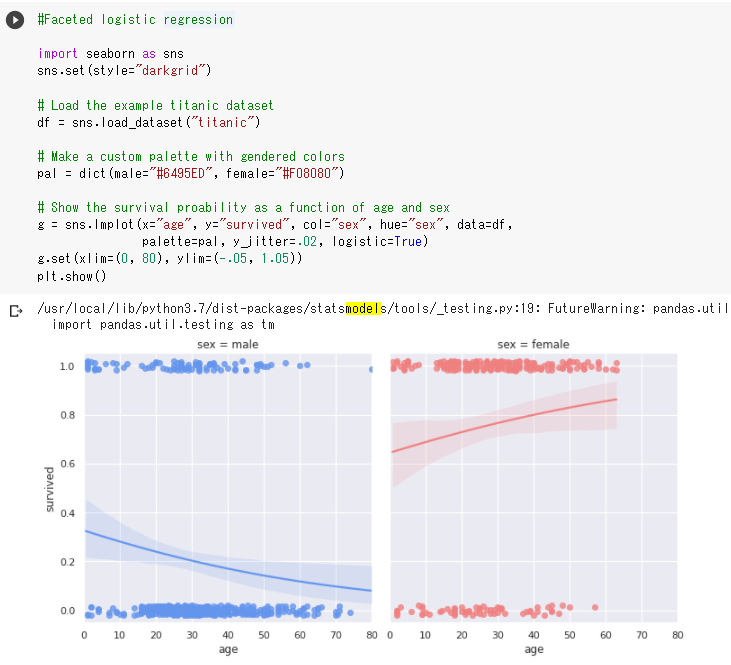
(5) seabornを使ってデータを見る2
・男性は年齢が高い方が生存率が低く、女性は年齢が高い方が生存率が高い
主成分分析(PCA)
§ 主成分分析とは ● 教師なし学習の1つ ● データから重要な成分をみつける手法 ● 主成分分析において重要な成分とはデータの分散が大きい成分であり この成分のことを主成分という ● 各主成分は互いに直行するように選ばれる § 主成分分析の特徴
● 少数変数を利用した分析や可視化(2・3次元の場合)を実現する
§ 第一主成分の主成分軸($u$)と分散($\sigma$)の求め方
1.データの中央化
各次元の平均値を各次元の各値($x_n$)より引く(中心点が原点になるように加工)
2.線形変換を行う
$x$を$u$方向に射影する
$z=u^Tx$
3.$z$(射影後のデータ)の分散を求める
$\sigma^2_z=\frac{1}{N}\displaystyle\sum^N_{n=1}(z_n-\bar{z})^2 (\bar{z}=0なので)$
$=\frac{1}{N}\displaystyle\sum^N_{n=1}(z_n)^2 (z=u^Txなので)$
$=\frac{1}{N}\displaystyle\sum^N_{n=1}(u^Tx)^2$
$=\frac{1}{N}\displaystyle\sum^N_{n=1}(u^Txx^Tu)^2 (内積の線形性より)$
$=u^T\left(\frac{1}{N}\displaystyle\sum^N_{n=1}(xx^T)^2\right)u$
$=u^T\Sigma u (この\Sigma は分散共分散行列)$
※分散共分散行列は正定値対象(固有値がすべて正の対称行列、固有ベクトルは直交)
4.$\sigma^2_z$の最大を求める(最適化したい値は$u$)
$arg$ $max$ $u^T\Sigma u ただしu^Tu=1(単位ベクトル)$
$u^T\Sigma u$は凸関数なので$\frac{\partial}{\partial u}(u^T\Sigma u)=0$で最大
以下ラグランジュ未定乗数法を用いて
$L(x,\lambda)=u^T\Sigma u-\lambda(u^Tu-1)$
$⇒\left\{\begin{array}{l}
\frac{\partial L}{\partial u}=\Sigma u-\lambda u = 0 ・・・① \
\frac{\partial L}{\partial \lambda}=u^tu-1 = 0 ・・・②
\end{array}
\right.$
①、②より
$\sigma^2_z=u^T\Sigma u=u^T(\lambda u)=\lambda u^Tu=\lambda$
これより$\lambda$は分散である
また①より$\Sigma u = \lambda u であり$
$uは \Sigma$の固有ベクトル(ただし単位ベクトル)$\lambda$は固有値となる
求めたかったのは最大の分散なので$\lambda$は最大固有値、
$u$はそれに対応した固有ベクトルとなる
§ 寄与率
第k主成分の分散の全分散に対する割合(第k主成分が持つ情報量の割合)
(第1~元次元分の主成分の分散は、元のデータの分散と一致する)
$\frac{第k主成分の分散}{主成分の総分散}$
§ 累積寄与率
第1-k主成分まで圧縮した際の情報損失量の割合
$\frac{第1~k主成分の分散の合計}{主成分の総分散}$
主成分分析 実装演習
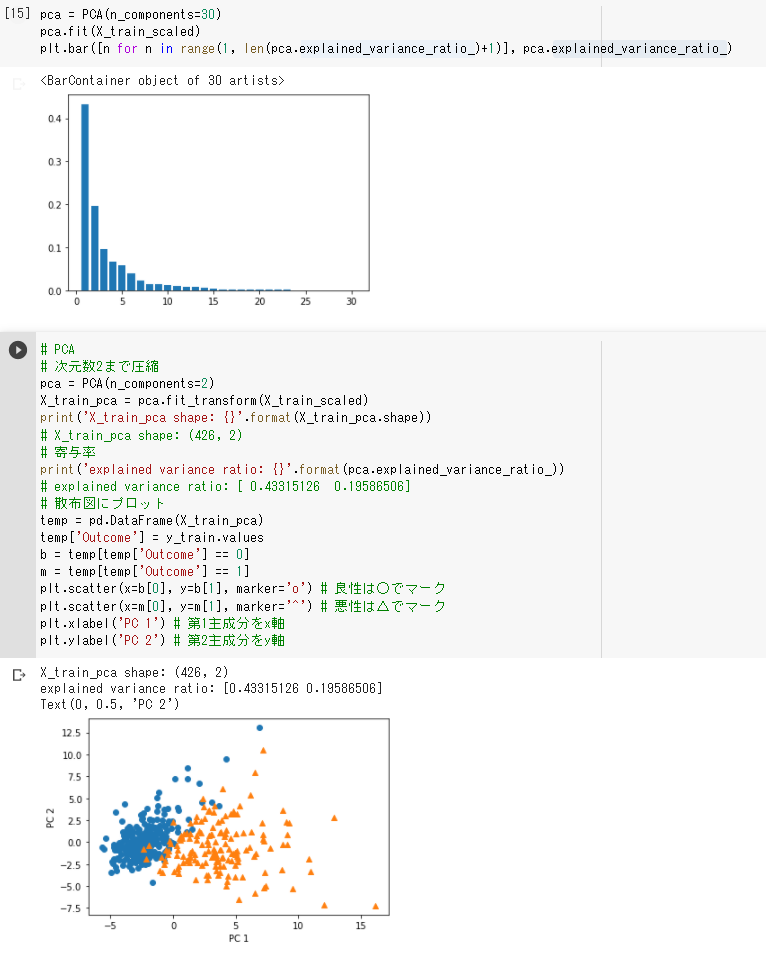
(1) ロジスティック回帰で判別 ・ LogisticRegressionCVでエラーが出るので引数にmax_iter=500を追加した ・ 1説明変数で判別しているが、訓練用でも検証用でも高いスコアが出ているように思う  (2) 主成分分析で判別
・ 第2成分までの累積寄与率はグラフより0.6くらいであると読み取れる
・ 次元数2まで圧縮しでいるが、それなりに判別が出来ているように見える
アルゴリズム
k-近傍法
§ k近傍法とは ● 最近傍のデータを$k$個取ってきて、それらがもっとも多く所属するクラスに識別  § k近傍法の特徴 ● kを変化させると結果も変わる  ● kを大きくすると決定境界は滑らかになる k-近傍法 実装演習
(1) KNeighborsClassifierを使う場合と使わない場合 ・ 上が使わなかった、下が使った方の結果。 結果に差異はないように見える。  (2) 最近傍のデータ数を3→30に変更して実行 ・ 上がKNeighborsClassifierを使わなかった、下が使った方の結果。 こちらも結果に差異はないように見える。 ・ 決定境界が滑らかになっている。 ・ 決定境界付近のデータは最近傍のデータ数を変えることで分類されるクラスが変わってしまう 決定境界付近のデータは分類結果の信頼性が低いのではないかと思う。 k-means
§ k-meansとは ● 教師なし学習 ● クラスタリング手法 ● 与えられたデータをk個のクラスに分類する § k-meansのアルゴリズム
1) 各クラスの中心の初期値を設定する
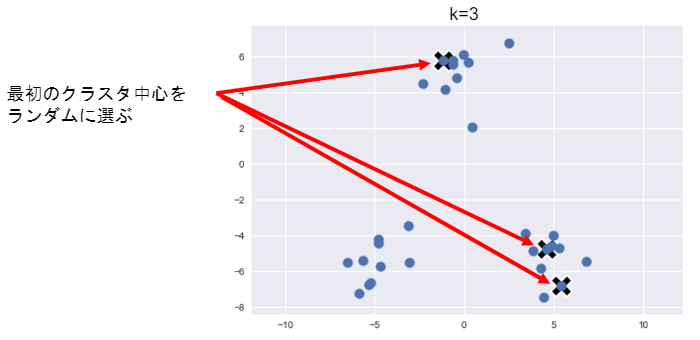
2) 各データ点に対して、各クラスタ中心との距離を計算し、
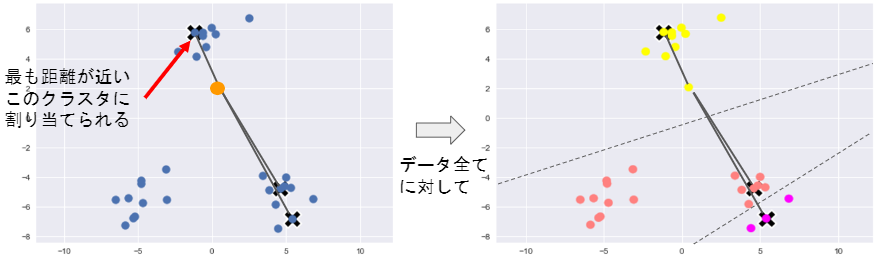
最も距離が近いクラスタを割り当てる
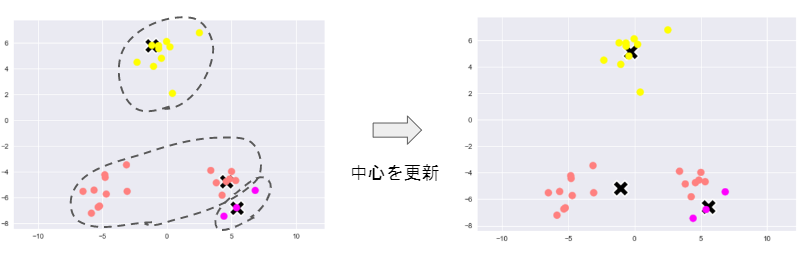
3) 各クラスタの平均ベクトル(中心)を計算する
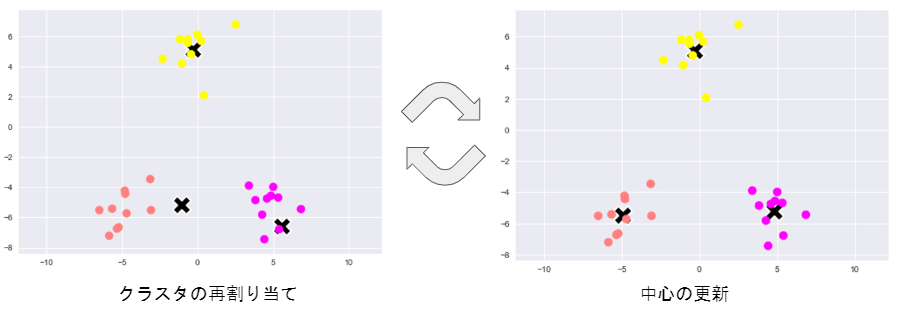
4) 収束するまで2, 3の処理を繰り返す
§ k-meansの特徴
● 中心の初期値を変えるとクラスタリング結果も変わりうる
初期値が離れるとうまくクラスタリングできるが
初期値が近いとうまくクラスタリングできない
● kの値を変えるとクラスタリング結果も変わる
§ より良好な解を得る工夫
● データを最初に割り当てるクラスターを変える
● クラスターの割り当てが収束するまでの処理を様々な条件で複数回行う
● 設定するクラスター数を多くする
§ k-means++
● k-meansの初期値の設定方法を改良したアルゴリズム
● 初期のクラスターの中心同士は離れていた方がよいという考え方に基づいて
設計されている
● 他の代表ベクトルとの距離の2乗に比例する確率を使って確率的に
代表ベクトルを選択(ルーレット選択)
k-means 実装演習
(1) KMeansを使わない場合 ● データがもとよりきれいに分かれているのできれいにクラス分けされている ● k-meansと直接関係はないが、デバッグするときにはデータ数を減らしてprint文で表示すると データがどのように処理されているか分かりやすかった  (2) KMeansを使った場合
● データがもとよりきれいに分かれているのできれいにクラス分けされている
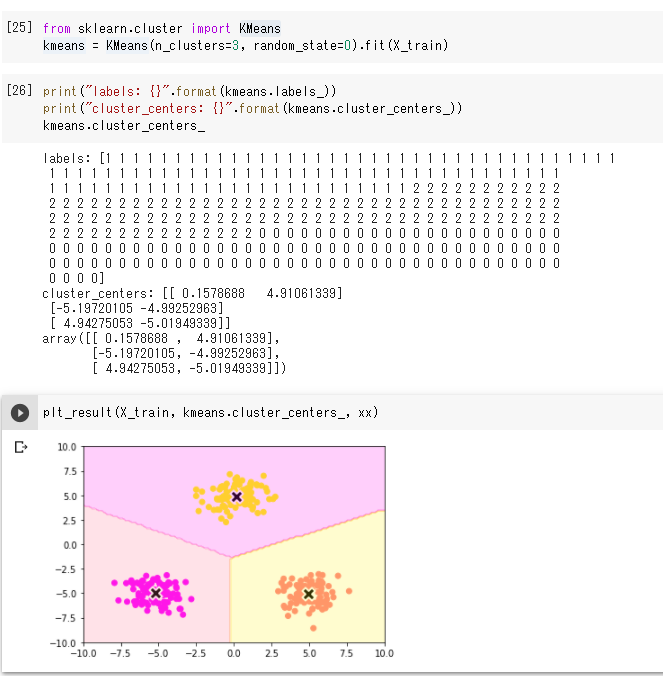
(3) クラス数を6にして実行してみる
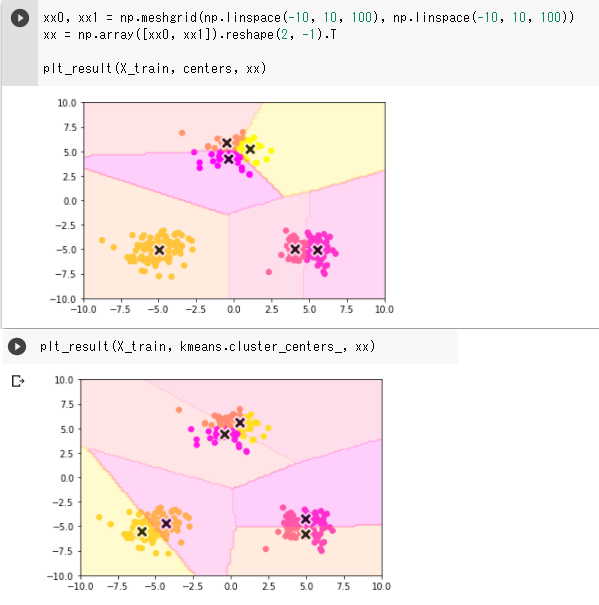
● 上がKMeansを使わない場合の結果、下がKMeansを使った場合の結果
先ほどと異なり2つの結果は違っている。(それぞれに再試行しても結果は変わらなかった)
これはランダムに初期化されたクラスタの中心が互いにことなるからではと考える。
サポートベクターマシン
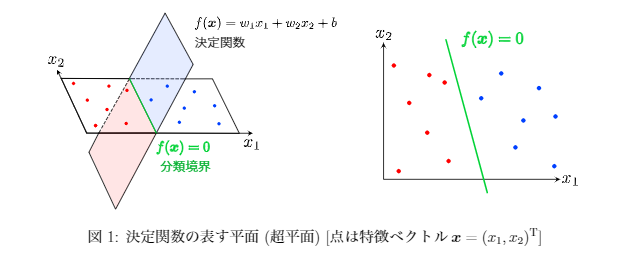
§ サポートベクターマシンとは ● 教師あり学習 ● 2クラス分類問題を扱う ● データを分類するための境界線を求めることで予測モデルを構築 ● 回帰問題や教師なし問題などへも応用されている ◆決定関数 ● 特徴ベクトル$x$がどちらのクラスに属するか判定するための関数 $f(x)=w^Tx+b$ ・ $x$(特徴ベクトル or 入力ベクトル)=与えられた入力データ ・ $w$は$x$と同じ次元の数値ベクトルであるが$f(x)$はスカラー ・ 決定関数より分類されて取るラベル$y$は以下で表される $y=sgn\,f(x)=\left\\{\begin{array}{l}+1 (f(x)>0) \\\ -1 (f(x)<0)\end{array}=y\right.$ ◆分類境界
● 特徴ベクトルを2つのクラスに分類する境界線
例)
$f(x)=(w_1 w_2)\left(\begin{array}{ccc}x_1\\x_2\end{array}\right)+b=w_1x_1+w_2x_2+b$
$f(x)$は以下の図の赤と青で塗られた平面を表す方程式で、
$x_1$軸と$x_2$軸で表される平面と交差している部分が分類境界となる
◆線形サポートベクトル分類
● 線形での分類
● マージン(分類境界を挟んで2つのクラスがどれくらい離れているか)を最大化する
● 訓練データより決定関数のパラメータ($w,b$)を決定する
◆線形サポートベクトル分類(ハードマージン)
● 特徴ベクトルが空間上できれいにクラスごとに分離できることを仮定したサポートベクトル分類
■ パラメータ($w,b$)の決定方法
・ 分類境界($f(x)=0$)と分類境界から最も近いデータ($x_i$)との距離の最大化を
考える
$f(x)$と$x_i$との距離$=\frac{|f(x)|}{||w||}=\frac{|w^Tx_i+b|}{||w||}$ $※||w||=\sqrt{w_1^2+w_2^2+・・・+w_n^2} $
ここでは分離可能なケース($y_if(x)>0$)を考えているので以下のように
変形できる
$\frac{|f(x)|}{||w||}=\frac{y_i[w^Tx_i+b]}{||w||}$
距離を最小化したいので
$\underset{i}{min}\frac{y_i[w^Tx_i+b]}{||w||}=\frac{1}{||w||}\underset{i}{min}\left[y_i[w^Tx_i+b]\right]≡\frac{M(w,b)}{||w||}$
$※ \underset{i}{min}\left[y_i[w^Tx_i+b]\right]≡\frac{M(w,b)}{||w||}$ とおく
$\underset{i}{min}\left[y_i[w^Tx_i+b]\right]$は分類境界から最も近いデータ($x_i$)との距離であり
この分類境界から最も近いデータ($x_i$)との距離を最大化=マージン最大化なので
$\underset{w,b}{max}\left[\underset{i}{min}\frac{y_i[w^Tx_i+b]}{||w||}\right]=\underset{w,b}{max}\frac{M(w,b)}{||w||}$ ・・・ サポートベクターマシンの目的関数
分類境界に一番近いデータ$x_i$・・・ サポートベクトル
この目的関数は次の2つの要素からできている
① 分類境界と分類境界に一番近いデータとの距離=マージン
⇔すべてのデータの分類境界との距離はマージン以上
$\underset{i}{min}\left[y_i[w^Tx_i+b]\right]=M(w,b) ⇔ y_i[w^Tx_i+b]≥M(w,b) … ①$
② マージンはできるだけ大きく取りたい
$\underset{w,b}{max}\frac{M(w,b)}{||w||} … ②$
【目的関数を計算しやすいように変形する】
$\tilde{w}=\frac{w}{M(w,b)}$ $\tilde{b}=\frac{b}{M(w,b)}$
↓ 分割するイメージ ↑
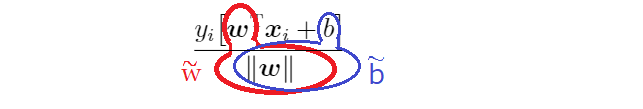
計算しやすいように$M(w,b)=1$とおく
$M(w,b)=1 であれば \tilde{w}=\frac{w}{M(w,b)}⇒\tilde{w}=w、 \tilde{b}=\frac{b}{M(w,b)}⇒\tilde{b}=b となるので$
$上の式①より \underset{i}{min}\left[y_i[\tilde{w}^Tx_i+\tilde{b}]\right]=1 ⇔ y_i[\tilde{w}^Tx_i+\tilde{b}]≥1$
$上の式②より \underset{\tilde{w},\tilde{b}}{max}\frac{1}{||\tilde{w}||}$
$\frac{1}{||\tilde{w}||}$の最大化は$||\tilde{w}||$の最小化と等価であることより
$\underset{\tilde{w},\tilde{b}}{min}\frac{1}{2}||\tilde{w}||^2 ※\frac{1}{2}倍や2乗しているのは後の計算のため・・・式②より$
◆線形サポートベクトル分類(ソフトマージン)
● 特徴ベクトルが空間上でクラスごとに分離できないことを仮定した
サポートベクトル分類
■ パラメータ($w,b$)の決定方法
● 式「①マージン」での制約条件 $y_i[\tilde{w}^Tx_i+\tilde{b}]≥1$ を緩和し
$y_i[w^Tx_i+b]≥1-\xi_i (i=1.・・・,n), \xi_i≥0$
$※\xi_i,$はマージン内に入るデータや誤分類されたデータに対する誤差を表す変数で
スラック変数と呼ばれる
● $\xi_i,$を考慮し、既出「②マージンはできるだけ大きく取りたい」で最終的に
求めた式を次のように変形する
$\underset{w,b,\xi}{min}\left[\frac{1}{2}||\tilde{w}||^2+C\displaystyle\sum^n_{i=1}\xi_i\right]$
$式の\underset{w,b}{min}\left[\frac{1}{2}||\tilde{w}||^2\right],部分はマージンの最大化の働きが$
$式の\underset{\xi}{min}\left[C\displaystyle\sum^n_{i=1}\xi_i\right],部分は分類誤差の最小化の働きがある$
$※ C$は正則化係数であり、正の定数で、ハイパーパラメータである。
また$C$は分類誤差の抑制の度合いを調整する。
$C$が大きいほどハードマージンの場合に近づき、$C→∞$で$\xi=0$になる
$C$が小さいほど誤分類を許容する
実装時にはデータに合わせてちょうど良い$C$の値を決定する必要がある
(交差検証法などを用いて決定する)
● $式①での制約条件 y_i[\tilde{w}^Tx_i+\tilde{b}]≥1 を緩和し$
◆サポートベクターマシンにおける双対表現
線形サポートベクトル分類で分類境界を決定するには以下の最適化問題を解けばよい
この最適化問題をサポートベクトル分類の主問題と呼ぶ
● ハードマージンの場合
$\underset{w,b}{min}\left[\frac{1}{2}||w||^2\right], y_i[w^Tx_i+b]≥1 (i=1.・・・,n)$
● ソフトマージンの場合
$\underset{w,b,\xi}{min}\left[\frac{1}{2}||w||^2+C\displaystyle\sum^n_{i=1}\xi_i\right], y_i[w^Tx_i+b]≥-1\xi_i, \xi_i≥0 (i=1.・・・,n)$
実際の計算はこれらの主問題ではなく、この主問題と等価な双対問題を解くことが
一般的
(理由は)
・ 主問題と比べて双対問題の方が変数を少なくできる
・ 分類境界の非線形化を考える上で双対問題の形式(双対形式)の方が有利となる
■ 双対問題の導出
● ラグランジュ関数の導入
ソフトマージンの最適化問題である
$\underset{w,b,\xi}{min}\left[\frac{1}{2}||w||^2+C\displaystyle\sum^n_{i=1}\xi_i\right], y_i[w^Tx_i+b]≥-1\xi_i, \xi_i≥0 (i=1.・・・,n)$
より、下記のラグランジュ関数を導入
$L(w,b,\xi,\alpha,\mu) = \frac{1}{2}||w||^2+c\displaystyle\sum^n_{i=1}\xi_i-\displaystyle\sum^n_{i=1}\alpha_i\left [y_i[w^Tx_i+b]-1+\xi_i \right] - \sum^n_{i=1}\mu_i\xi_i$
※ 式変形のイメージは下記の通り
ラグランジュ関数の赤丸の部分は目的関数、青丸の部分($\sum$も含めて)は
制約条件
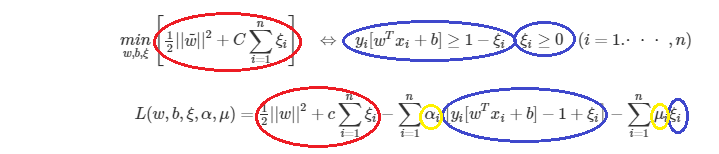
・ $\alpha_i≥0,\alpha=(\alpha_1,・・・,\alpha_n)^T, \mu_i≥0,\mu=(\mu_1,・・・,\mu_n)^T$
・ 元々の最適化問題に登場する変数$,w,,b,,\xi,$は主変数
・ 新たに導入した変数$,\alpha,,\mu,$は双対変数
このラグランジュ関数に関する次の最適化問題のことを双対問題という
$\underset{\alpha,\mu}{max},\underset{w,b,\xi}{min},L(w,b,\xi,\alpha,\mu)$
● 双対問題
$\underset{\alpha,\mu}{max},\underset{w,b,\xi}{min},L(w,b,\xi,\alpha,\mu)$
・主変数に関して最小化($\underset{w,b,\xi}{min},L(w,b,\xi,\alpha,\mu)$)
$(1) \frac{\partial}{\partial w}L(w,b,\xi,\alpha,\mu)=w-\displaystyle\sum^n_{i=1}\alpha_iy_ix_i=0⇒w=\displaystyle\sum^n_{i=1}\alpha_iy_ix_i$
$(2) \frac{\partial}{\partial b}L(w,b,\xi,\alpha,\mu)=-\displaystyle\sum^n_{i=1}\alpha_iy_i=0$
$(3) \frac{\partial}{\partial \xi_i}L(w,b,\xi,\alpha,\mu)=C-\alpha_i-\mu_i=0 (i=1,・・・,n)$
・双対変数に関して最大化($\underset{\alpha,\mu}{max},L(w,b,\xi,\alpha,\mu)$)
(1)~(3)をラグランジュ関数へ代入し式を整理すると
$\underset{\alpha}{max}\left\{ -\frac{1}{2}\displaystyle\sum^n_{i=1}\sum^n_{i=1}\alpha_i\alpha_jy_iy_jx^Tx+\displaystyle\sum^n_{i=1}\alpha_i \right\}, \displaystyle\sum^n_{i=1}\alpha_iy_i=0, 0≤\alpha_i<C(i=1,・・・,n)$
となり、$\alpha$のみの最適化問題に置き換えることができる
(上記の式はソフトマージンの場合、ハードマージンの場合は、
$0≤\alpha_i<C$ の部分が $0≤\alpha_i$ となる)
● 主問題と双対問題の関係
・あらゆる最適化問題で「双対問題の最適値は主問題の最適値以下となる」
(弱双耐性)
・サポートベクトル分類の場合は、主問題=双対問題が成立する(強双耐性)
※ サポートベクトル分類での主問題
$\underset{w,b,\xi}{min},\underset{\alpha,\mu}{max},L(w,b,\xi,\alpha,\mu)$
・主変数$(w,b,\xi)$においては極小点、双対変数$(\alpha,\mu)$においては極大点
= ラグランジュ関数の鞍点 がサポートベクトル分類での最適解
◆カーネルを用いた非線形分類への拡張
● 直線で分離できないデータを、線形分離ができるように高次元空間へと拡張
(写像)する。下図のようなイメージ($\phi(x):(x_1,x_2)→(x_1,x_2,x_1^2,x_2^2)$で写像)
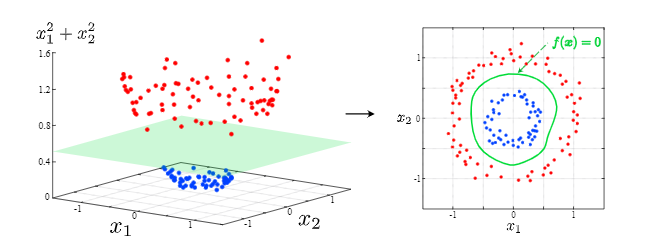
● 双対問題での目的関数を拡張する
$\underset{\alpha}{max}\left\{ -\frac{1}{2}\displaystyle\sum^n_{i=1}\sum^n_{i=1}\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)+\displaystyle\sum^n_{i=1}\alpha_i \right\}, \displaystyle\sum^n_{i=1}\alpha_iy_i=0, 0≤\alpha_i(i=1,・・・,n)$
● カーネル関数で置き換える
$\phi(x_i)^T\phi(x)$の内積部分の計算が膨大になるためカーネル関数で置き換える
$\underset{\alpha}{max}\left\{ -\frac{1}{2}\displaystyle\sum^n_{i=1}\sum^n_{i=1}\alpha_i\alpha_jy_iy_j K(x_i,x_j)+\displaystyle\sum^n_{i=1}\alpha_i \right\}, \displaystyle\sum^n_{i=1}\alpha_iy_i=0, 0≤\alpha_i(i=1,・・・,n)$
● 決定関数もカーネル関数で置き換える
$f(x)=w^T\phi(x)+b=\displaystyle\sum^n_{i=1}\alpha_iy_iK(x_i,x)+b$
カーネル関数を使えば最適化や決定関数の計算に$\phi(x)$が不要になる
● 代表的なカーネル関数
$⇒\left\{\begin{array}{l}
多項式カーネル :K(x_i,x_j)=[x_i^Tx_j+c]^d \
ガウス(RBF)カーネル:K(x_i,x_j)=\exp(-\gamma||x_i-x_j||^2)\
シグモイドカーネル :K(x_i,x_j)=\tanh(bx_i^Tx_j+c)
\end{array}
\right.$
サポートベクターマシン 実装演習
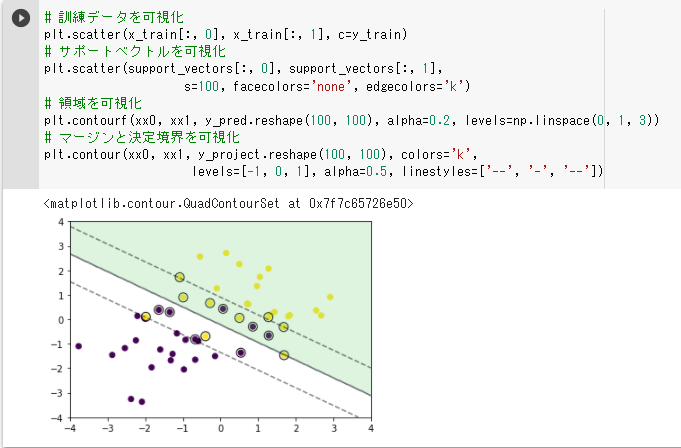
(1)線形分離可能(ハードマージン) ・以下の結果では分類に成功しているが、学習率eta1の値のみ大きくするとサポートベクトルが 決定境界とほぼ同じになった ・同じく、学習率eta2の値のみ大きくすると分類に失敗した → 2つの学習率はバランスが重要だと思われる  (2)線形分離不可能
・見た目は線形分離可能と全く異なるが、学習、予測部分のロジックは殆ど変わらない
実際のプログラムではif文を使用すれば1実装で線形分離可能/不可能を実装できるように思う
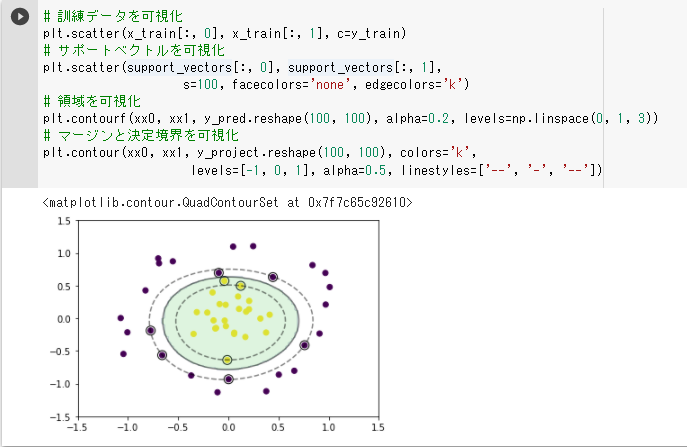
(3)データ重なりあり(ソフトマージン)
・以下はパラメータC=1でテストしたが
パラメータCを小さく(0.01)するとマージンが大きくなり、
パラメータCを大きく(10)するとマージンは小さくなった
・パラメータCを100→1000と大きくしても10の時と変わらなかったが
(a = np.clip(a, 0, C) がその理由だと考える)
パラメータCをどんどん小さくしていくとマージンもどんどん広がっていった
→ 誤差の許容を最小限にする場合は簡単だが、誤差の許容をどこまで大きくするかは
試行錯誤する必要がある