PyODE のスライダ(ode.SliderJoint)にてバネに働く力(バネ係数とか)を任意関数で設定できるか試してみました。
前の記事です → PyODE スライダーを2重にしてみる
1 動機
この手の物理エンジン使った計算例というものは、
・要素数が多め( 10 個で少ないほうかな)
・バネやダンパなんかは一番単純なもの。
といった具合のものが常です。
しかし私はバネ・ダンパ系を扱う目的です。
単純な線形バネしか設定できないのでは意味がない。
果たしてODE(PyODE)でバネ係数を任意設定することは可能でしょうか。
これがもし駄目だったらODEの利用はいったんあきらめることになります。
先に結論
各時刻ごとに、「slideJoint」のインスタンスメソッド「 addForce() 」から任意の力を値で渡せることがわかりました。
したがってバネ係数や減衰を好きな特性に設定できます。
2 設定方法
スライダに生じる力を直接設定
まずスライダーに生じる力を値で渡す部分です。↓
while() : #### 時間進行のループ
#中略
f = spring( j01 , KP, KD )
j01.addForce( f )
world.step(dt)
j01 というのはスライダすなわち ode.SliderJoint インスタンスです。
後述のspring()という自作関数で決めた値を f としてます。
メソッド addForce で任意の値を駆動力として与えられます。
world.step() が ode の1ステップの時間進行ですから
その直前とかで addForce を呼べばよいでしょう。
スライダの状態から力を決める
spring() は、スライダの状態から力を得る自作の関数です。
def spring( j, kp, kd=None ):
r = j.getPosition()
f = r*r*r * kp
if None is not kd:
f += j.getPositionRate() * kd
return - f
ここではjがスライダ(ode.SliderJoint インスタンス)
スライダの変位量はインスタンスメソッドgetPosition()で取得できます。
同じく変位速度はgetPositionRate()です。
ここでは変位の3乗に比例した反発力が生じるバネとしました。
( 2 乗で試したところ線形バネとの違いが不明瞭に見えたため 3 乗にした。)
※ これらのコーディングにより、単純な線形バネではC/C++側にあった処理がPythonコード側に移ったことになります。
なにがしかのパフォーマンス低下はありえます。
3 結果
黒丸が固定オブジェクト。
線はバネ(スライダ)の位置をあらわしています。
赤茶丸がバネの上に乗って揺れています。
↓ こちらは赤茶丸の高さと速度それぞれの時間変化。
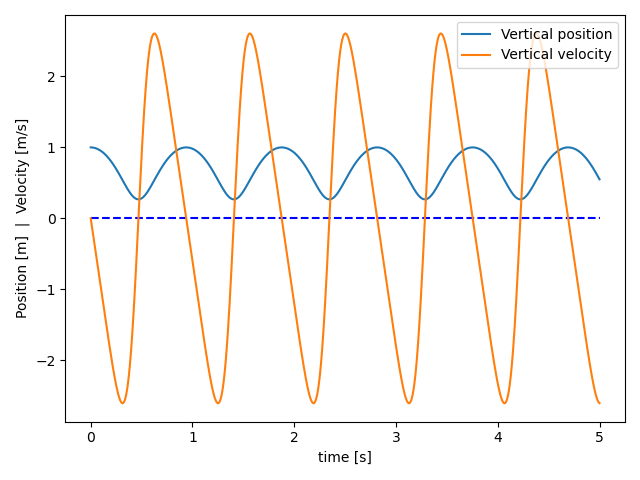
KP = 100.0 KD = 0としています。
非線形にした甲斐あって
正弦波とは違った、歪んだ波形が見られます。
4 総括
addForce() で力を好きに設定できることがわかりました。
これならいろいろと試せそうです。
ということで、しばらくこの PyODE を使っていこうと思います。