Confusion Matrixは、日本語では混同行列などいくつかの名前で呼ばれます。機械学習の分類タスクで結果が出てきたら、まずConfusion Matrixを作成して、全体の様子を可視化するといいでしょう。
Confusion Matrix
・ わかりやすい
・ 単純だけど、奥深い
・ 異なった分類モデル間の比較など、応用が利く
結果が 0 または 1 に分類される、二値分類の例を使ってConfusion Matrixの使い方を少し見てみましょう。
<ケース1>
さてここでは、合計200個のサンプルがあるとします。
0 の教師ラベルがついたもの 100個
1 の教師ラベルがついたもの 100個 => 異常サンプルとします
それぞれのサンプルには、機械学習で計算したスコアがついています。
スコアの数値を使って、教師ラベル = 1 の、異常サンプルを検出できるかどうかを考えてみます。
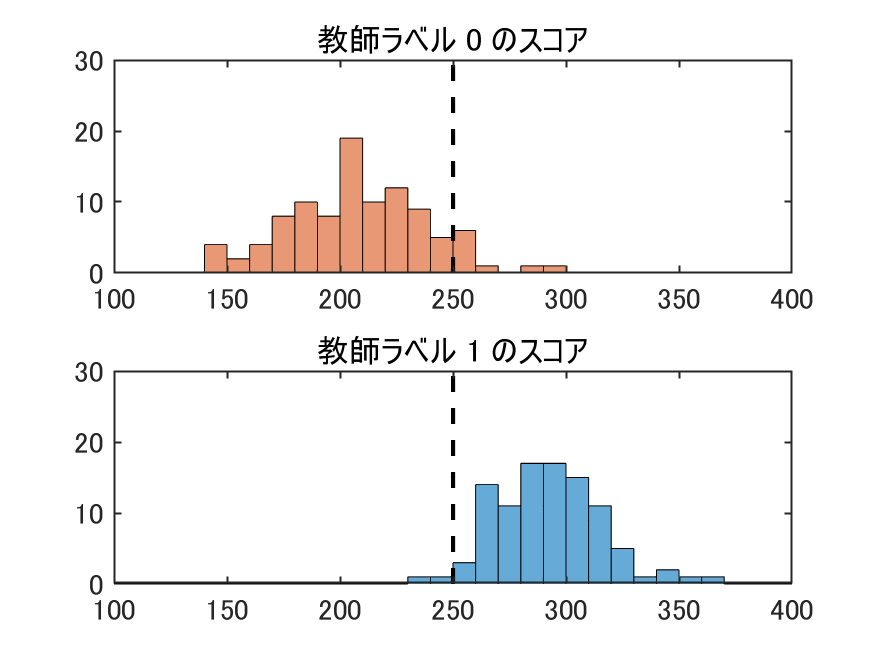
スコア250を境に、それより大きい場合を1、小さい場合を0として判別しました。上のヒストグラムで、点線のところがスコア250です。
結果を、Confusion Matrixを使って表現してみます。

教師ラベル = 1, 予測ラベル = 1 と、正しく検出できたのは98個で、 教師ラベル = 1 のうちの、98 % を見つけることができるようです。ただし、教師ラベル = 1, 予測ラベル = 0 の False Negative (見逃し)は 2個となっています。
Accuracy 0.94
Recall 0.98
Precision 0.90
F1 Score 0.94
(見やすいように 2桁で表示してあります)
教師ラベル = 0, 予測ラベル = 1、つまり、False Positive(過検出)は9個で、予測ラベル = 1で検出されたもの(98 + 9 で 107個 )の中では 8.4 % となっています。検出されていても、だいたい10個に一個は正常なんですね。
ケース1では、教師ラベル = 1 と、教師ラベル = 0 が同じ数ずつあるということでConfusion Matrixを作っていますが、実世界では、正常サンプルと異常サンプルが1:1ということがあまりありません。たいていは、大量の正常サンプルの中に異常サンプルが少し混入しているでしょう。
<ケース2>
次の例では、ケース1と同じ性質のサンプルを使って、
0 の教師ラベルがついたもの1000個
1 の教師ラベルがついもの 100個
合わせて合計1100個のサンプルから、1を検出することを考えてみます。
ケース1と同じく閾値スコア 250で判別して、Confusion Matrixを描いてみました。


Accuracy 0.92
Recall 0.98
Precision 0.56
F1 Score 0.71
となります。右上の部分、過検出が77個と多くなってしまいます。
予測ラベル = 1で検出されたものの56 % は正解ですが、半分近くの、44 % が過検出です。こんなに過検出が多くては困るので、閾値を上げてみましょうか。
<ケース3>
たとえば、スコア閾値を290に上げてみましょう。そうすると、


過検出はぐっと少なくなって、53 + 5 = 58個中の5個ですから 9 % 程度にまで減ったことになります。
Accuracy 0.95
Recall 0.53
Precision 0.91
F1 Score 0.67
ただし、見逃しも増えます。教師ラベル = 1 の 100個のうち47個、つまり異常品のうち半分近くの 47 % を見逃すことになります。見逃しが多いのは困りものですね。
過検出と見逃しは、シーソーの左右に物が乗っているみたいに、片方を少なくしようとすると、もう片方が多くなる、というものです。そこで、適切な閾値設定で、バランスがよいところに落ち着かせることを考えることになります。
閾値の決め方については、いろいろな観点や方法があります。数値の上でここがよいということだけではなく、過検出に対する対処をどうするか、見逃しがあってもどれくらいなら大丈夫なのか、など全体のプロセスの考え方を組み入れていきます。
たとえば、検出されたものに対して、次の工程で人が目で見て、異常品と正常品をより分けることが考えられます。ケース2では、過検出が多いとはいえ、確率的に2個に1個は異常なものがあるのですから、たくさんのサンプルから、たまに(10個に1個)出る異常品を人が最初から探すよりはやりやすいのでは、と考える場合もあるでしょう。
・過検出、見逃し以外にも、上にあるAccuracy、Recall 、Precision 、F1 Score という表現がよく使われます。1 - Recall = 見逃し率、 1 - Precision = 過検出率になります。(注)習慣によっては、サンプル全体の数を分母にして計算することがあります。
・閾値の決め方について、ROC曲線やAUCについてもぜひ一読ください