・SincNetフィルタは簡単
・視覚的に理解したい
・音声などの波形データに使える
SincNetフィルタとは
SincNetは、音声などの波形データを分類するモデルで、最初の処理に、SincNetフィルタとよばれる、sinc関数による畳み込み(波形なので、基本的には一次元の畳み込み)が入るものです。SincNetフィルタの出力は、その後は通常のニューラルネットワークといっしょに使われます。
2019年にラバネッリさんらカナダの研究者が発表したもので、中身を見ると、うーん賢い!なんでもっと早く開発されていなかったんだろう?と思います
https://arxiv.org/abs/1808.00158
sinc関数
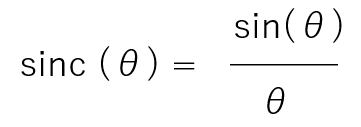
sinc関数というのは、上のような形をしたごくシンプルな関数です θ の代わりに x と書いてある場合や、πxと書いてあることもありますが、単にθでもよくて、角度θの正弦(sin関数)を角度θで割ったものです
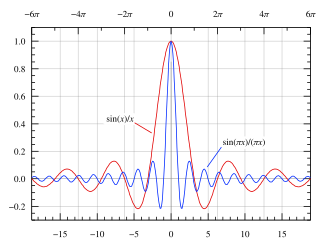
https://ja.wikipedia.org/wiki/Sinc%E9%96%A2%E6%95%B0
sinc関数の式の見た目は、θ = 0 付近が大きくて、だんだん両端に行くにしたがってサイン波が小さくなる形をしています このsinc関数は周波数空間では矩形関数に対応するという性質を持っています
SincNetフィルタでは、sinc関数で作ったバンドパスフィルタ(上下のカットオフ周波数が決まっている)を周波数域ごとに作り、これを、全体の周波数をカバーするバンドパスフィルタのシリーズとして使います
バンドパスフィルタの作成
バンドパスフィルタをつくるときは、sinc関数が持つθにつく係数f(=周波数)を変えて二つ作り、下のように引き算するだけです。
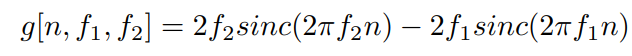
https://arxiv.org/pdf/1808.00158.pdf
f1 や f2 はバンドパスフィルタの上下の周波数です 2 × π × f × n が上のsinc関数の θ になりますね
論文の説明が少し丁寧すぎるのですが、中身はとても簡単な式なんですね このバンドパスフィルタは、周波数空間では、ほぼきれいに矩形(四角形)になります
最後に、
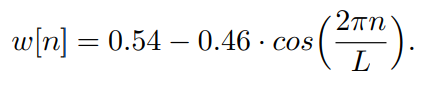
上の式を使って左右の両端が上手く減衰するようにラップをかけると、このような形になり、SincNetフィルタのできあがりです
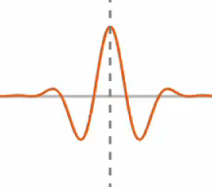
周波数フィルタをかけてみよう
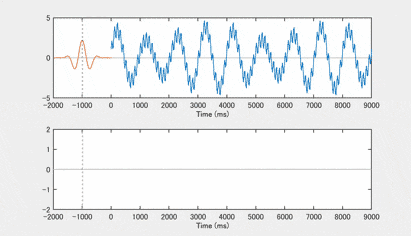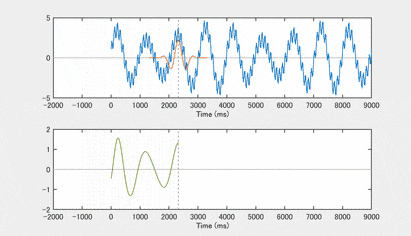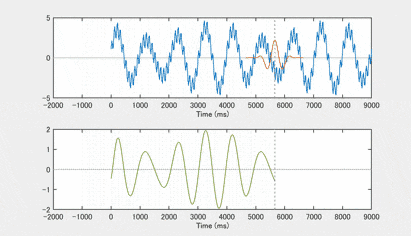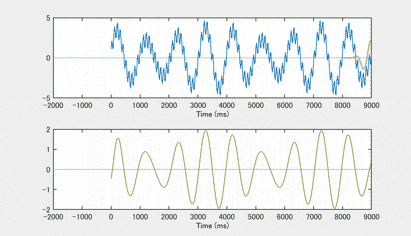
では、これを適当な周波数の混合で作った合成波形(上の段)に、畳み込みでかけてみましょう 次の図の下の段は、畳み込みの結果です キザキザ部分が取れいて low pass filter として働いているのがわかりやすいと思います
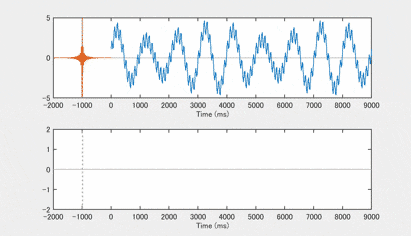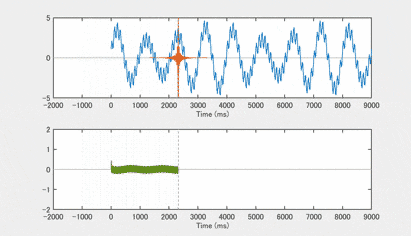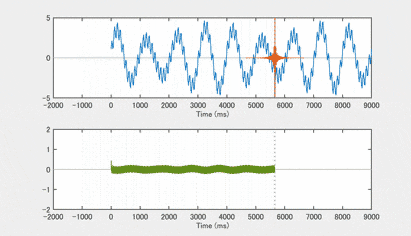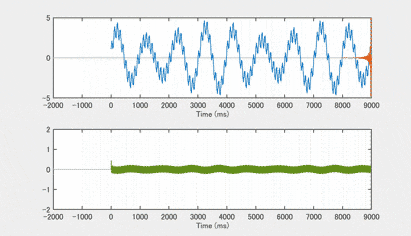
試しにhigh pass 部分のバンドパスフィルタを作って畳み込みをかけてみると、こんな感じになります high pass filterは、性質上、低周波成分を完全に除くのは難しいですが、高周波成分がメインになっているのがわかるでしょうか
良い点
sinc関数は単純ですし、sinc関数の中の、周波数に関わる係数を指定するだけで、バンドパスフィルタが作れる、という優れものです
バンドパスフィルタの幅を決めれば、フーリエ変換に比べて情報量をぐっと圧縮できるし、畳み込み演算は、フーリエ変換・逆変換より単純で時間が早くて、ここもうれしい点ですね
使われている
わたしは、SincNetを、1年ほど前にひょんなこと(※)から知ったのですが、この1年の間にもWeb検索でSincNetの名前をヒットする件数がどんどん増えており、いろいろな分野で使われはじめているようです SincNetフィルタの出力を、ニューラルネットワークにつないで(波形を)分類する例が多いようですが、他の方法でも応用ができそうな気がします
周波数解析に使うFIRフィルタは、設計がとても大変なのですが、SincNetフィルタならば、設計も楽ですし、フィルタの挙動も、わりと計算で推測できそうです SincNetやSincNetフィルタは、今後も応用例が増えていくだろうと思われます
youtubeのリンク(Mirco Ravanelliさんによる説明)
https://www.youtube.com/watch?v=mXQBObRGUgk
論文へのリンク
https://arxiv.org/abs/1808.00158
(※)脳波の解析に使ってました