・ データの内容からふたつのグループに分ける
・ ガウスモデルで近似
・ 共分散行列
データを分ける
ここでは、2変量データを、ふたつのグループに分けることをしてみます(クラスタリング)。
ひとつめのデータは簡単そうです。青グループと、赤グループ(実際は橙色)は離れているので、分けやすそうです。

混合ガウスモデル
混合ガウスモデルのクラスタリングを使って分けてみます。教師なし学習の一種なのですが、グループの数を指定する必要があります。「ガウスモデルを2個使ってフィッティング」を指示すると、このようにきれいに二つに分けてくれます。

実は、青のデータと、赤のデータは、もともとガウスモデル(正規分布に由来するモデル)に少し手を加えてノイズを入れて作ってあるもので、混合ガウスモデルで上手くフィッティングできます。
今回使ったのは、MATLAB Statistics and Machine Learning Toolbox という、統計と機械学習モデルのツールボックスです。けっこういろいろなものが入っていて、わりとお世話になってます。
重なりがある場合
二個目のデータは、次の図でみるように特徴的な分布をしています。何年か前に、こういうデータを見たことがあり、どうするんだろう? という場面がありました。
実際のデータは人の運動の測定から出てきたもので、測定を含む、もっと複雑な経緯でできたものです。ここでは簡単にガウス分布をベースに共分散行列と呼ばれる 2 × 2 の行列を使って、似たようなものを作っています。
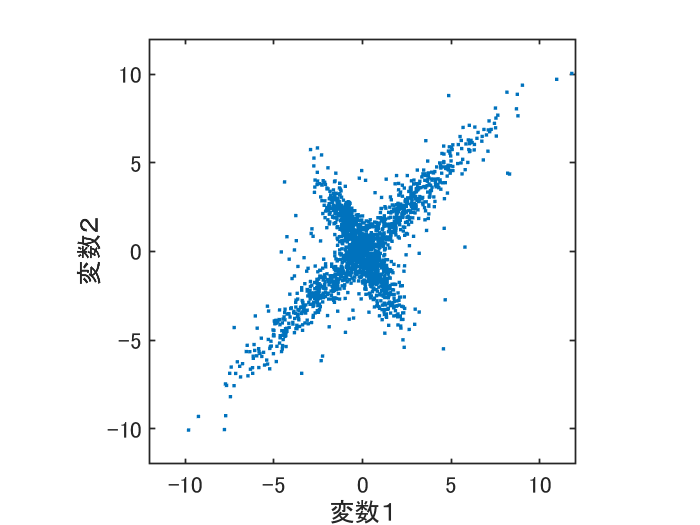
クラスタリングには、上と同じように混合ガウスモデルを利用して計算してみます。
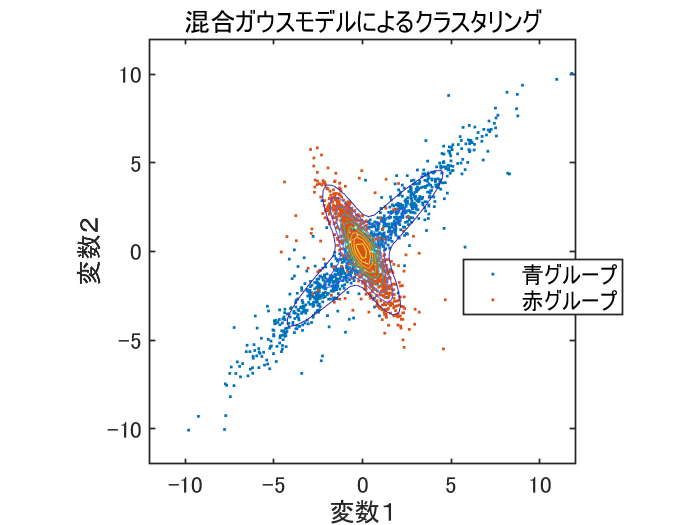
データがふたつのグループに分けられてて、青グループのガウスモデルと、赤グループのガウスモデルが、上手いことフィッティングされているように見えます。しかし、ここでふと疑問が。赤グループと、青グループが重なり合っている真ん中らへんはどうするんでしょう? ある点が、赤グループか、青グループか、なんてわかるんでしょうか?
重なりをどうする?
真ん中の重なった部分に関しては、どちらのグループに属するかがわかりませんね。試しに、出てきたクラスタリングモデルの結果を見てみると、ちょうど上手く半分ずつになるように割り当ててあり、双方のグループは、おおむね両方とも1000個ずつのグループになっていました。
どう利用する?
真ん中の部分がきれいにグループに分かれないのに、クラスタリングする意味があるかどうか? と思われるかもしれません。このデータを使っていたときは、クラスタリングの結果を元にシミュレーションを作ることにしたんです。詳しくは長くなるのでここには書けませんが、青と赤、それぞれのガウスモデルの共分散行列から、シミュレーションで疑似データを生成して使うことができました。
教師なし学習は、データの内容そのものから規則性を見つけることで、クラスタリングなどが主な手法になると思います。宝探しみたいな側面があって、教師なし学習の結果からデータの特徴をみつけたときは、とても面白かった記憶があります。