Go to Qiita Advent Calendar 2024 Top
LoginSignup
3
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@emattsan(Eiji MATSUMOTO)in株式会社永和システムマネジメント

どう書くE04「ドキドキ登山〜怒りのデスルート」を解いたアイディアの解説

Posted at

問題はこちら：

何かタイトルが違う気もしますが、あまり気にしないでください。

実装はこちら：

戦略

  1. 入力の石の位置を、現在の石の状態とデスルートの状態の初期状態とします
  2. 横径に対して上から順に
    1. 横径が現在の石の状態と重なる場合
      • 横径に対して、現在の石の状態の位置と反対側の位置を新しい石の状態にする
      • 現在のデスルートの状態に、新しい石の状態の位置を加えたものを新しいデスルートの状態にする
    2. 横径が現在の石の状態と重ならない場合
      • 現在のデスルートの状態の、横径の両端に位置するルートを入れ替えたものを新しいデスルートの状態にする
  3. すべての横径に対して 2. を適用した結果のデスルートが登山に失敗するルートになるので、全登山者のルートからデスルートを除いたものが登頂に成功するルートになる

この戦略の利点は、次のような点です。

  • 山頂から山麓へ一回の走査で結果を導ける
  • 石の状態とデスルートの状態のそれぞれの現在の状態だけを覚えておけばよい

例

次のような例を考えています。

test("345132:C", "ACGH")

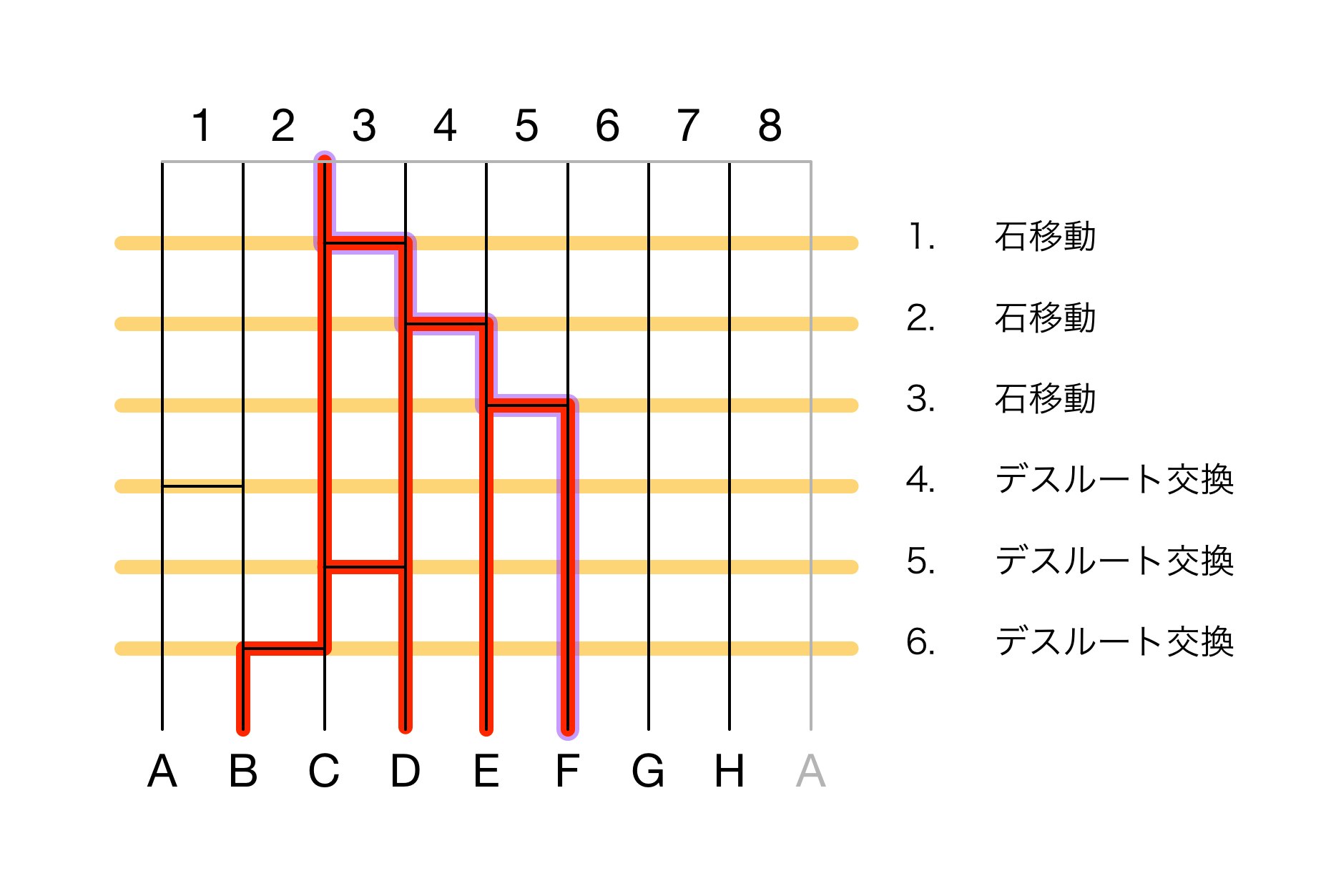
これを上の考え方に基づいて描き下してみたものが次の図になります。円で書くのが面倒だったので上端を山頂とした直交座標で描いてます。
ここで赤い線がデスルート、その中の紫の縁取りがしてあるルートが落石ルートです。

ドキドキ登山.jpg

  1. C の位置が石の初期状態です。デスルートにも {C} を設定します。
  2. 3 の横径は現在の石の位置 C と重なるので、石の位置は D に移動します。デスルートにも D が追加され {C, D} になります。
  3. 4 の横径は現在の石の位置 D と重なるので、石の位置は E に移動します。デスルートにも E が追加され {C, D, E} になります。
  4. 5 の横径は現在の石の位置 E と重なるので、石の位置は F に移動します。デスルートにも F が追加され {C, D, E, F} になります。
  5. 1 の横径は現在の石の位置 F と重ならないので、A と B を交換しますがどちらもデスルートに含まれないので、デスルートは変化せず {C, D, E, F} のままです。
  6. 3 の横径は現在の石の位置 F と重ならないので、C と D を交換しますがどちらもデスルートに含まれるので、デスルートは変化せず {C, D, E, F} のままです。
  7. 2 の横径は現在の石の位置 F とは重ならないので、B と C を交換します。B がデスルートに含まれず、C がデスルートに含まれるので、B をデスルートに加え、C をデスルートから外します。結果、デスルートは {B, D, E, F} になります。
  8. 全登山者からデスルートの最後の状態である {B, D, E, F} を除いた {A, C, G, H} が求める結果になります。

定義してみる

入力を次のように定義した場合、

x_1 \, x_2 \, x_3 \, \cdots \, x_n \, {\rm :} \, c

(x_i \in \{1, 2, 3, 4, 5, 6, 7, 8\},
c \in \{{\rm A}, {\rm B}, {\rm C}, {\rm D}, {\rm E}, {\rm F}, {\rm G}, {\rm H} \})

次のように定義される result をアルファベット順に連結した文字列が求める結果になります。

\begin{eqnarray}
rock_0 & = & \{c\} \\
route_0 & = & \{c\} \\
branch_i & = & B(x_i) \\
\\
B(x) & = &
  \begin{cases}
    \{{\rm A}, {\rm B}\} & (x = 1) \\
    \{{\rm B}, {\rm C}\} & (x = 2) \\
    \{{\rm C}, {\rm D}\} & (x = 3) \\
    \{{\rm D}, {\rm E}\} & (x = 4) \\
    \{{\rm E}, {\rm F}\} & (x = 5) \\
    \{{\rm F}, {\rm G}\} & (x = 6) \\
    \{{\rm G}, {\rm H}\} & (x = 7) \\
    \{{\rm H}, {\rm A}\} & (x = 8)
  \end{cases} \\
\\
rock_i & = &
  \begin{cases}
    branch_i - rock_{i-1} & (branch_i \cap rock_{i-1} \ne \emptyset) \\
    rock_{i-1} & (branch_i \cap rock_{i-1} = \emptyset)
  \end{cases} \\
\\
route_i & = &
  \begin{cases}
    route_{i-1} \cup branch_i & (branch_i \cap rock_{i-1} \ne \emptyset) \\
    route_{i-1} \oplus branch_i & (branch_i \cap rock_{i-1} = \emptyset, |route_{i-1} \cap branch_i | = 1) \\
    route_{i-1} & (branch_i \cap rock_{i-1} = \emptyset, otherwise))
  \end{cases} \\
\\
\\
result & = & \{{\rm A}, {\rm B}, {\rm C}, {\rm D}, {\rm E}, {\rm F}, {\rm G}, {\rm H} \} - route_n \\
\\
 & & (ただし、 1 \leq i \leq n) \\
\end{eqnarray}

また、次のように rock と route を組みにすると畳み込みが簡単になります。

\begin{eqnarray}
\{rock_0, route_0\} & = & \{\{c\}, \{c\}\} \\
\{rock_n, route_n\} & = &
  \begin{cases}
    \{branch_i - rock_{i-1}, route_{i-1} \cup branch_i \} & (branch_i \cap rock_{i-1} \ne 0) \\
    \{rock_{i-1}, route_{i-1} \oplus branch_i\} & (branch_i \cap rock_{i-1} = 0, |route_{i-1} \cap branch_i| = 1) \\
    \{rock_{i-1}, route_{i-1}\} & (branch_i \cap rock_{i-1} = 0, otherwise)
  \end{cases}
\end{eqnarray}

この問題では要素の数が有限なので、要素が存在する/しないをビットの 0/1 に割り当てることでビット演算でも容易に表現することができます。
その場合、今回のケースでは差と排他的論理和が同じ結果になるので、差の代わりに排他的論理和を利用するとビット演算で扱いやすくなります。

\begin{eqnarray}
rock_i & = & branch_i \oplus rock_{i-1} \, (branch_i \cap rock_{i-1} \ne \emptyset)
\end{eqnarray}

実装

Ruby

Ruby での実装例です。Ruby の Array は標準では排他的論理和が定義されていないので、最初に演算子 Array#^ を定義しています。

orde04.rb
class Array
  def ^(other)
    (self | other) - (self & other)
  end
end

def b(x)
  case x
  when '1' then ['A', 'B']
  when '2' then ['B', 'C']
  when '3' then ['C', 'D']
  when '4' then ['D', 'E']
  when '5' then ['E', 'F']
  when '6' then ['F', 'G']
  when '7' then ['G', 'H']
  when '8' then ['H', 'A']
  end
end

def solve(input)
  xs, c = input.split(':')

  rock = [c]
  route = [c]

  xs.chars.each do |x|
    branch = b(x)
    unless (branch & rock).empty?
      rock = branch - rock
      route |= branch
    else
      if (route & branch).one?
        route ^= branch
      end
    end
  end

  result = [*'A'..'H'] - route

  result.sort.join
end

Prolog

いつものように。Prolog での実装。
rock と route を組みにして扱っています。

orde04.prolog
% Set operations
intersection(XS, YS, ZS) :- findall(N, (member(N, XS), member(N, YS)), ZS), sort(ZS).
union(XS, YS, ZS) :- findall(N, (member(N, XS); member(N, YS)), ZS), sort(ZS).
difference(XS, YS, ZS) :- findall(N, (member(N, XS), \+(member(N, YS))), ZS), sort(ZS).
exclusive_or(XS, YS, ZS) :- union(XS, YS, US), intersection(XS, YS, IS), difference(US, IS, ZS).

% branches
b(0'1, "AB").
b(0'2, "BC").
b(0'3, "CD").
b(0'4, "DE").
b(0'5, "EF").
b(0'6, "FG").
b(0'7, "GH").
b(0'8, "HA").

% rolling rock
roll([Rock, Route], [], [Rock, Route]).
roll([RockIn, RouteIn], [Branch|Branches], [RockOut, RouteOut]) :-
  \+(intersection(Branch, RockIn, [])),
  difference(Branch, RockIn, RockTmp),
  union(RouteIn, Branch, RouteTmp),
  roll([RockTmp, RouteTmp], Branches, [RockOut, RouteOut]),
  !.
roll([RockIn, RouteIn], [Branch|Branches], [RockOut, RouteOut]) :-
  intersection(Branch, RouteIn, [_]),
  exclusive_or(RouteIn, Branch, RouteTmp),
  roll([RockIn, RouteTmp], Branches, [RockOut, RouteOut]),
  !.
roll([RockIn, RouteIn], [_|Branches], [RockOut, RouteOut]) :-
  roll([RockIn, RouteIn], Branches, [RockOut, RouteOut]),
  !.

solve(Input, Living) :-
  append(BS, [0':, Rock], Input),
  maplist(b, BS, Branches),
  roll([[Rock], [Rock]], Branches, [[_], Dead]),
  difference("ABCDEFGH", Dead, Living).

judge(_, Expected, Expected) :-
  format(".", []),
  !.
judge(Input, Expected, Actual) :-
  format("~ninput:    ~s~nexpected: ~s~nactual:   ~s~n", [Input, Expected, Actual]),
  !.

test(Input, Expected) :-
  solve(Input, Actual),
  judge(Input, Expected, Actual).

main :-
  test("2512:C", "DEFGH"),
  test("1:A", "CDEFGH"),
  test(":C", "ABDEFGH"),
  test("2345:B", "AGH"),
  test("1256:E", "ABCDH"),
  test("1228:A", "ADEFG"),
  test("5623:B", "AEFGH"),
  test("8157:C", "ABDEFGH"),
  test("74767:E", "ABCFGH"),
  test("88717:D", "ABCEFGH"),
  test("148647:A", "ACDEFH"),
  test("374258:H", "BCDEFH"),
  test("6647768:F", "ABCDEH"),
  test("4786317:E", "ABFGH"),
  test("3456781:C", ""),
  test("225721686547123:C", "CEF"),
  test("2765356148824666:F", "ABCDEH"),
  test("42318287535641783:F", "BDE"),
  test("584423584751745261:D", "FGH"),
  test("8811873415472513884:D", "CFG"),
  test("74817442725737422451:H", "BCDEF"),
  test("223188865746766511566:C", "ABGH"),
  test("2763666483242552567747:F", "ABCG"),
  test("76724442325377753577138:E", "EG"),
  test("327328486656448784712618:B", ""),
  test("4884637666662548114774288:D", "DGH"),
  test("84226765313786654637511248:H", "DEF"),
  test("486142154163288126476238756:A", "CDF"),
  test("1836275732415226326155464567:F", "BCD"),
  test("62544434452376661746517374245:G", "G"),
  test("381352782758218463842725673473:B", "A"),
  format("~n", []),
  !.

GNU Prolog で実行。

$ gprolog
| ?- ['orde04.prolog'].
yes
| ?- main.
...............................
yes
3
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?