「オフラインリアルタイムどう書くE02」に参戦しました。
今回のお題はこちら。
参加された皆さんのコードはこちらからたどることができます。
どう書くには早すぎたProlog
当日はPrologで挑戦したのですが、敗退しました。Prologはまだ早すぎました。自分のProlog力のレベルを測る意図もあって試みてみたのですが、予選参加資格の選考で落ちるぐらいのレベルでしかありませんでした。
心残りは「Prolog遅い」みたいな印象を与えてしまったのではないかということ。
その後、他の参加者のアイディアを反芻しつつ、帰りの電車の中で考えていました。
コンパクトにすればもっと早くなるのではというアイディアの解き方
基本的なアイディアは、条件に合う矩形を抜き出してその面積を比べて最小最大を抽出する、という力技な方法。ただ62x62の範囲から闇雲に矩形を抽出しようとするとひどく時間がかかってしまう。
電車の中で考えていたのは、図にはかなりの隙間があるということ。これを取り除いてコンパクトにすれば、抽出しなければならない矩形の数もそれなりに少なくなるだろうと期待できます。
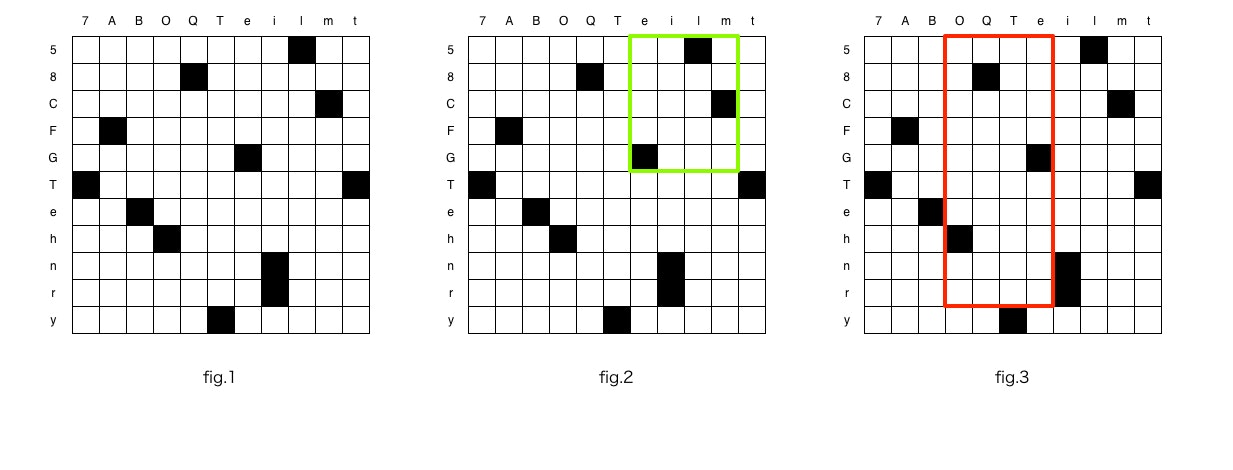
例題の図をもとにコンパクトにした図を書いてみると fig.1 のようになります。そして最小の範囲は fig.2 で表現できる最小の範囲、最大の範囲は fig.3 で表現できる最大の範囲になります。
fig.2 で表現できる範囲のうち最小の範囲は、それぞれの位置の文字から計算できます。
つまり、
- 左端は
eの位置 - 右端は
mの位置 - 上端は
5の位置 - 下端は
Gの位置
なので、
min_area = (pos('m') - pos('e') + 1) * (pos('G') - pos('5') + 1)
で求めることができます。ここで pos(c) は文字の位置(インデクス)を返す関数です。
fig.3 で表現できる範囲のうち最大の範囲を求める場合は、それぞれの位置の外側を調べなければなりません。
つまり、
- 左端は 'O' の左のセル('B')の位置の一つ右
- 右端は 'e' の右のセル('i')の位置の一つ左
- 上端は '5' の上のセル … はないので 0 とする
- 下端は 'r' の下のセル('y')の位置の一つ上
となり、
max_area = (pos('i') - 1 - pos('B') - 1 + 1) * (pos('y') - 1 - 0 + 1)
で求めることができます。
それでも抽出しなければならない矩形の数は少なくないですが、62x62の範囲から抽出するのに比べればだいぶ少なくなったはずです。
どう書く Haskell
これを踏まえて。Haskell で実装してみました。
data.txt はサンプルデータを空白区切のテキストデータとして保存したファイルです。
$ ghc --make orde02pire.hs
Linking orde02pire ...
$ time ./orde02pire data.txt
...............................................
real 0m1.659s
user 0m1.640s
sys 0m0.016s
正直な感想は、「思ったより早くならなかった」。
当日の発表ですでにかなり早い実装が披露されていたので、もうちょっと善戦できるんぢゃないかと期待したんですが、そもそも矩形の数えが挙げという方法では高速化は難しいのかもしれません(ちゃんと調べていませんが)。
開催日当日の夜にアイディアをまとめ、コードにできたのは翌日になってから。ここにアップしたコードはその後に少し整理したものです。
module Main where
import System.Environment
import System.IO
import Data.Char
import Data.List
split = words.map (\c -> if c == ',' then ' ' else c)
axis c
| '0' <= c && c <= '9' = ord c - ord '0'
| 'A' <= c && c <= 'Z' = ord c - ord 'A' + 10
| 'a' <= c && c <= 'z' = ord c - ord 'a' + 10 + 26
divideInput =
(\(n, sq) -> (n, map (\[x, y] -> (axis x, axis y)) sq)).(\(n, (_:sq)) -> (read n::Int, split sq)).break (== ':')
circumscribing_area (x0, y0, x1, y1) =
(x1 - x0 + 1) * (y1 - y0 + 1)
inscribing_area xaxis yaxis (x0, y0, x1, y1) =
(ix1 - ix0 + 1) * (iy1 - iy0 + 1)
where
ix0 = case takeWhile (< x0) xaxis of [] -> 0; s -> last s + 1
iy0 = case takeWhile (< y0) yaxis of [] -> 0; s -> last s + 1
ix1 = case dropWhile (<= x1) xaxis of [] -> 61; s -> head s - 1
iy1 = case dropWhile (<= y1) yaxis of [] -> 61; s -> head s - 1
solve input =
if rectangles == []
then "-"
else concat [show $ minimum $ map circumscribing_area rectangles, ",", show $ maximum $ map (inscribing_area xaxis yaxis) rectangles]
where
(count, points) = divideInput input
xaxis = sort $ nub $ map fst points
yaxis = sort $ nub $ map snd points
rectangles =
[ (x0, y0, x1, y1)
| x0 <- xaxis
, y0 <- yaxis
, x1 <- dropWhile (< x0) xaxis
, y1 <- dropWhile (< y0) yaxis
, count == length [ 1
| (x, y) <- points
, x0 <= x && x <= x1 && y0 <= y && y <= y1
]
]
test [input, expected] =
if actual == expected
then putStr "."
else putStrLn $ concat
[ "\ninput: ", input
, "\nexpected: ", expected
, "\nacutal: ", actual
]
where
actual = solve input
main = getArgs >>= return.head >>= flip openFile ReadMode >>= hGetContents >>= mapM_ (test.words).lines >> putStrLn ""
data.txt の冒頭の5行。計測に使ったファイルはサンプルデータの47行を入れています。
3:Oh,Be,AF,in,eG,ir,l5,Q8,mC,7T,Ty,tT 108,1920
3:00,zz,0z,z0 -
1:ho 1,3844
2:am -
4:00,zz,0z,z0 3844,3844
どう書くProlog
Haskell で書いて解き方が理解できたので。当日惨敗したPrologに翻訳してみました。
$ gplc orde02pire.pro
$ time ./orde02pire data.txt
...............................................
real 0m3.338s
user 0m3.327s
sys 0m0.006s
Prologでもこれぐらいの速さで解けるのです、というのを主張しておきます。
:- initialization(main).
% 文字列を , で分割
split(Input, [Point|Points]) :-
append(Point, [0',|Rest], Input),
split(Rest, Points),
!.
split(Point, [Point]).
% 文字から位置へ変換
code_position(C, P) :- between(0'0, 0'9, C), P is C - 0'0.
code_position(C, P) :- between(0'A, 0'Z, C), P is C - 0'A + 10.
code_position(C, P) :- between(0'a, 0'z, C), P is C - 0'a + 36.
% 文字の組から XY 座標の値に変換
dot_point([Dx, Dy], [X, Y]) :-
code_position(Dx, X),
code_position(Dy, Y).
% 入力の文字列を分解
divide_input(Input, Count, Points) :-
append(N, [0':|Sequence], Input),
number_codes(Count, N),
split(Sequence, Dots),
maplist(dot_point, Dots, Points).
% XY 座標の値を X と Y に分割
point_xy([X, Y], X, Y).
% XY 座標のリストを X 座標のリストと Y 座標のリストに分割
points_axes(Points, Xaxis, Yaxis) :-
maplist(point_xy, Points, XS, YS),
sort(XS, Xaxis),
sort(YS, Yaxis).
% 左上右下の範囲に含まれる点の座標を取得する
included_point([X0, Y0, X1, Y1], Points, [X, Y]) :-
member([X, Y], Points),
between(X0, X1, X),
between(Y0, Y1, Y).
% 左上右下の範囲の面積
circumscribing_area([X0, Y0, X1, Y1], Area) :-
Area is (X1 - X0 + 1) * (Y1 - Y0 + 1).
% 指定した点の位置の内側にある点の位置の一つ外側の位置、ただし内側に点がない場合は最小値
inside_outside(Axis, P, I) :-
append(_, [P1, P|_], Axis),
I is P1 + 1.
inside_outside([P|_], P, 0).
% 指定した点の位置の外側にある点の位置の一つ内側の位置、ただし外側に点がない場合は最大値
outside_inside(Axis, P, I) :-
append(_, [P, P1|_], Axis),
I is P1 - 1.
outside_inside(Axis, P, 61) :-
append(_, [P], Axis).
% 左上右下の範囲の外側の最大の面積
inscribing_area([X0, Y0, X1, Y1], Xaxis, Yaxis, Area) :-
inside_outside(Xaxis, X0, IX0),
inside_outside(Yaxis, Y0, IY0),
outside_inside(Xaxis, X1, IX1),
outside_inside(Yaxis, Y1, IY1),
Area is (IX1 - IX0 + 1) * (IY1 - IY0 + 1).
% 指定した個数の点を含む矩形(左上右下の位置)を得る
points_rectangle(Xaxis, Yaxis, Count, Points, [X0, Y0, X1, Y1]) :-
append(_, [X0|XS], Xaxis),
append(_, [Y0|YS], Yaxis),
append(_, [X1|_], [X0|XS]),
append(_, [Y1|_], [Y0|YS]),
findall(P, included_point([X0, Y0, X1, Y1], Points, P), PS),
length(PS, Count).
% 問題を解く
solve(Input, Output) :-
divide_input(Input, Count, Points),
points_axes(Points, Xaxis, Yaxis),
findall(R, points_rectangle(Xaxis, Yaxis, Count, Points, R), Rectangles),
findall(A, (member(R, Rectangles), circumscribing_area(R, A)), CircumscribingAreas),
findall(A, (member(R, Rectangles), inscribing_area(R, Xaxis, Yaxis, A)), InscribingAreas),
min_list(CircumscribingAreas, MinArea),
max_list(InscribingAreas, MaxArea),
number_codes(MinArea, Min),
number_codes(MaxArea, Max),
append(Min, [0',|Max], Output).
solve(_, "-").
% 以下、テスト用のコード
judge(_, Expected, Expected) :- write('.').
judge(Input, Expected, Actual) :- format("~ninput: ~s~nexpected: ~s~nactual: ~s~n", [Input, Expected, Actual]).
test(Input, Expected) :-
solve(Input, Actual),
judge(Input, Expected, Actual).
test(end_of_file).
test(Line) :-
append(Input, [0' |Expected], Line),
test(Input, Expected),
!.
read_line_to_code(_, -1, end_of_file).
read_line_to_code(_, 0'\n, []).
read_line_to_code(Stream, Code, [Code|Codes]) :-
read_line_to_codes(Stream, Codes), !.
read_line_to_codes(Stream, Codes) :-
get_code(Stream, Code),
read_line_to_code(Stream, Code, Codes).
main :-
current_prolog_flag(argv, [_,Filename|_]),
open(Filename, read, Stream),
repeat,
read_line_to_codes(Stream, Line),
test(Line),
Line == end_of_file,
close(Stream),
nl,
halt.
どう書くC++
もっと高速に結果を出せるんぢゃないかと期待していたのにそれほどでもなかったので、C++に翻訳して高速化をはかってみました(間違った努力)。
当日参加された皆さんのアイディアも反映し、重複する数え上げとかをできるだけ排除する形に書いてみました。
$ g++ --std=c++11 -o orde02pire orde02pire.cpp
$ time ./orde02pire data.txt
...............................................
real 0m0.037s
user 0m0.031s
sys 0m0.003s
二桁ぐらいは早くなった。
もう少し早くならないかと最適化オプションを指定してみた(間違った高速化の努力)。
$ g++ --std=c++11 -O3 -o orde02pire orde02pire.cpp
$ time ./orde02pire data.txt
...............................................
real 0m0.012s
user 0m0.007s
sys 0m0.002s
今の私の力量ではこれが限界か。
# include <algorithm>
# include <iostream>
# include <fstream>
# include <sstream>
# include <string>
# include <vector>
# include <set>
# include <limits>
# include <numeric>
int axis(char c)
{
c -= '0';
if(c > 9) c -= 7;
if(c > 36) c -= 6;
return c;
}
typedef std::vector<int> Axis;
typedef std::set<int> AxisSet;
struct Point
{
int x;
int y;
Point(int x, int y) : x(x), y(y) {}
};
typedef std::vector<Point> Points;
struct Rectangle
{
int left;
int top;
int right;
int bottom;
Rectangle(int left, int top, int right, int bottom) : left(left), top(top), right(right), bottom(bottom) {}
int circumscribing_area(const Axis& xaxis, const Axis& yaxis) const
{
return (xaxis[right] - xaxis[left] + 1) * (yaxis[bottom] - yaxis[top] + 1);
}
int inscribing_area(const Axis& xaxis, const Axis& yaxis) const
{
int x0 = (left == 0) ? 0 : xaxis[left - 1] + 1;
int y0 = (top == 0) ? 0 : yaxis[top - 1] + 1;
int x1 = (right == xaxis.size() - 1) ? 62 : xaxis[right + 1];
int y1 = (bottom == yaxis.size() - 1) ? 62 : yaxis[bottom + 1];
return (x1 - x0) * (y1 - y0);
}
};
typedef std::vector<Rectangle> Rectangles;
class ShrunkenPoints
{
public:
ShrunkenPoints(const std::vector<Point>& points, const Axis& xaxis, const Axis& yaxis) :
xaxis_size_(xaxis.size() + 1),
yaxis_size_(yaxis.size() + 1),
count_points_((xaxis.size() + 1) * (yaxis.size() + 1))
{
std::vector<int> xindices(62);
std::vector<int> yindices(62);
for(int i = 0; i < xaxis.size(); ++i)
{
xindices[xaxis[i]] = i;
}
for(int i = 0; i < yaxis.size(); ++i)
{
yindices[yaxis[i]] = i;
}
std::vector<int> dots(xaxis.size() * yaxis.size());
for(auto i = points.begin(); i != points.end(); ++i)
{
dots[yindices[i->y] * xaxis.size() + xindices[i->x]] = 1;
}
for(int x = xaxis.size() - 1; x >= 0; --x)
{
for(int y = yaxis.size() - 1; y >= 0; --y)
{
count_points(x, y) = dots[y * xaxis.size() + x]
+ count_points(x + 1, y)
+ count_points(x, y + 1)
- count_points(x + 1, y + 1);
}
}
}
int count_points(int x0, int y0, int x1, int y1) const
{
return count_points(x0, y0) - count_points(x1 + 1, y0) - count_points(x0, y1 + 1) + count_points(x1 + 1, y1 + 1);
}
private:
int& count_points(int x, int y)
{
return count_points_[y * xaxis_size_ + x];
}
int count_points(int x, int y) const
{
return count_points_[y * xaxis_size_ + x];
}
const int xaxis_size_;
const int yaxis_size_;
std::vector<int> count_points_;
};
std::string solve(const std::string& input)
{
std::istringstream iss(input);
int n;
char separator;
iss >> n >> separator;
Points points;
AxisSet xaxis_set;
AxisSet yaxis_set;
while(iss.good())
{
char cx;
char cy;
iss >> cx >> cy >> separator;
int x = axis(cx);
int y = axis(cy);
points.push_back(Point(x, y));
xaxis_set.insert(x);
yaxis_set.insert(y);
}
Axis xaxis(xaxis_set.begin(), xaxis_set.end());
Axis yaxis(yaxis_set.begin(), yaxis_set.end());
Rectangles rectangles;
ShrunkenPoints shrunken_points(points, xaxis, yaxis);
for(int ix0 = 0; ix0 < xaxis.size(); ++ix0)
{
for(int iy0 = 0; iy0 < yaxis.size(); ++iy0)
{
for(int ix1 = ix0; ix1 < xaxis.size(); ++ix1)
{
for(int iy1 = iy0; iy1 < yaxis.size(); ++iy1)
{
if(shrunken_points.count_points(ix0, iy0, ix1, iy1) == n)
{
rectangles.push_back(Rectangle(ix0, iy0, ix1, iy1));
}
}
}
}
}
if(rectangles.empty())
{
return "-";
}
auto min_rectangle = [&](int n, const Rectangle& r) { return std::min(n, r.circumscribing_area(xaxis, yaxis)); };
auto max_rectangle = [&](int n, const Rectangle& r) { return std::max(n, r.inscribing_area(xaxis, yaxis)); };
int min = std::accumulate(rectangles.begin(), rectangles.end(), std::numeric_limits<int>::max(), min_rectangle);
int max = std::accumulate(rectangles.begin(), rectangles.end(), std::numeric_limits<int>::min(), max_rectangle);
std::ostringstream oss;
oss << min << "," << max;
return oss.str();
}
void test(const std::string& input, const std::string& expected)
{
std::string actual = solve(input);
if(actual == expected)
{
std::cout << ".";
}
else
{
std::cout
<< "\ninput: " << input
<< "\nexpected: " << expected
<< "\nactual: " << actual
<< "\n";
}
}
int main(int, char* argv[])
{
std::ifstream ifs(argv[1]);
std::string line;
while(std::getline(ifs, line).good())
{
std::string input;
std::string expected;
std::istringstream(line) >> input >> expected;
test(input, expected);
}
std::cout << std::endl;
return 0;
}