RustとNomで電卓を作る

目次

1. はじめに
2. 環境構築
3. AST実装
4. パーサ実装
5. 入出力実装
6. 終わりに

はじめに

皆さんこんにちは！
Rust言語はお好きですか？ もちろん好きですよね。
Rustを知らない？ ではRustの素晴らしい点を挙げて紹介してみることにしましょう。

Rustの特徴は以下の通りです。

• Mozillaが応援している言語
• 2006年から開発が始まった新しめの言語
• 2016年、2017年、2018年、2019年、2020年のStack Overflow Developer Surveyで「最も愛されているプログラミング言語」で一位を獲得している
• C/C++と同等の処理速度
• C/C++の代替えを目指している
• 静的に型が付く、コンパイラ言語
• 静的に変数の寿命もわかり、自動でメモリを解放（GCより速い！）
• 関数内部限定での極めて賢い型推論
• C/C++と比べて極めて安全
• オブジェクト指向ではないし関数型言語でもない新たな概念を持つ
• デフォルトでスレッドセーフが保証された変数達
• C++のムーブセマンティクスを言語レベルでサポート
• C++と違い、制約付きのテンプレートがある
• DSL作成可能で健全なマクロ
• タプル、代数的データ型とマッチ式もあります
• 標準でテスト機能が付いている
• 標準でパッケージマネージャーがある

素晴らしい言語ですね！勉強しない手はありません。
では、どのように勉強すればいいのでしょうか。

簡単です。四則演算の数式を計算する電卓を作るのです。(?)

これは、Rust初級者or中級者向けを想定しています。
少々難しいかもしれませんが、Rustに関する解説はあまりしません。（代わりに参照URLを記載したりしています）
私が解説するよりも、既に存在する素晴らしいドキュメントを読んだ方が効率的だからです。

流れを紹介します。

まずはRustの開発環境、プロジェクト作成をします。
そして次は、四則演算の数式の構文構造をデータ構造として定義していきます。
次に、4+5*(1/10)等の数式の文字列を解析して、定義したデータ構造へ変換するパーサというものを実装していきます。
最後に入出力インタフェースを実装して完成です。

[今回作る電卓の完成ソースコードはこちらで確認できます]
https://github.com/elipmoc/rust-calc

環境構築

まずはRustをインストールしましょう。
Rustのバージョンは1.37.0という仮定で話を進めていきます。

Rustのインストール方法はコチラを参照してください
https://www.rust-lang.org/

インストールが完了するとcargo, rustc, rustupという三つのプログラムがシェルやcmd, powershell等で使えるようになっています。
-Vでそれぞれバージョン確認できますので確認してみましょう。

$ rustc -V
rustc 1.37.0 (eae3437df 2019-08-13)

$ rustup -V
rustup 1.18.3 (435397f48 2019-05-22)

$ cargo -V
cargo 1.37.0 (9edd08916 2019-08-02)

それぞれ軽く説明しますと、

• rustcはRustのコンパイラ

• rustupはRustのコンパイラをバージョン管理するツール

• cargoはRustのパッケージマネージャー

では、早速プロジェクトを作成していきます。

rust_calcという名前でプロジェクト作成。

cargo new rust_calc

rust_calcというフォルダが生成されるので、中身を確認してください。

• Cargo.toml

• src/main.rs

の二つのファイルがあります。

Cargo.tomlはプロジェクトの設定を書くファイルです。
src/main.rsがmain関数を定義するRustのソースファイルとなります。

Cargo.tomlに今回必要になるライブラリを先に書いていきます。
[dependencies]の所にnom="5"と書きましょう。

[package]
省略

[dependencies]
nom="5"

プロジェクトの配下でcargo runコマンドを打って実行してみましょう。
Hello, world!が表示されるのを確認してください。

この時、素晴らしいことにCargo.tomlの更新を目ざとく検知して、nomライブラリが
自動でダウンロードされ、インストールされているのに気が付くでしょう。npm iよりも遥かに便利ですね。(npmとはnode.jsという言語のパッケージマネージャーです)

AST実装

はじめに、四則演算の数式の構文の構造をデータ構造として定義していきたいと思います。
まず、数式は木構造として定義することができます。
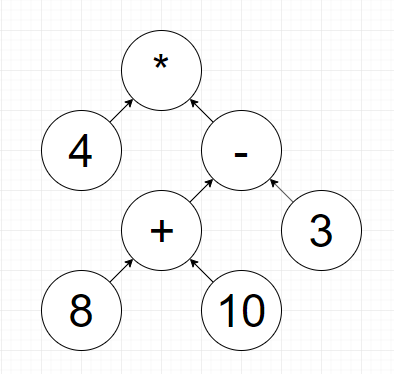
以下の画像を見てください。

これは4*((8+10)-3)という数式を木構造に変換したものです。
このように数式の構文は木構造へと変換することが可能です。
注意すべきポイントは()は木の深さで表現されていることです。元の数式で最も()のネストが深い8+10は木構造で一番下に来るようにすることで優先順位の表現を可能にしています。

このように作った、構文を構成する必要最低限の要素だけを表現した木構造を抽象構文木(abstract syntax tree　略してAST)と呼びます。

ASTの概念もだいたい理解したところで、早速、数式のASTをRustで定義していきましょう。

src/にcalcフォルダを作成。

src/にcalc.rsファイルを作成。

calc/にast.rsファイルを作成。

calc.rsにpub mod ast;と記述し、ast.rsをcalcより上の階層でも使えるように公開します。
Rustではモジュールを公開するのにpub修飾子を付けます。

ではast.rsに数式のASTを定義していきます。

定数のAST

とりあえず、最も簡単な定数の構造を定義します。

ast.rsに書いていきましょう。

///定数を表す
pub struct ConstantVal(pub i32);

実際にmain.rsで使ってみます。

pub mod calc;

fn main() {
    let a=calc::ast::ConstantVal(33);
    println!("ConstantVal={}",a.0);
}

main.rsでpub mod calc;することで、mainの子モジュールとしてcalcモジュールを登録することでcalcモジュールを使用できるようにしています。
今回の場合pubを付けなくても動きますが、後で行うドキュメント自動生成のためにあえて公開にしています。

このコードはConstantValを生成して、中身の33をa.0で表示するだけのものです。簡単ですね！

ところで、ちょっとだけConstantValに問題があります。
このConstantValは不変なものとして扱いたいと思っているのですが……。

pub mod calc;

fn main() {
    let mut a=calc::ast::ConstantVal(33);
    a.0=25;
    println!("ConstantVal={}",a.0);
}

このようにmutを付ければ、中の値を書き換えれてしまいます。
設計上あまりよくないので、中の値を変えれないようカプセル化しておきましょう。

ast.rsを修正

///定数を表す
pub struct ConstantVal(i32);

これでコンパイルすると外部からは中の要素にアクセスできないため、生成することはできなくなりました。

次にそれをなんとかするために関数を実装していきます。

ast.rsを修正。

///定数を表す
pub struct ConstantVal(i32);

impl ConstantVal {
    ///ConstantValを生成する
    pub fn new(val: i32) -> ConstantVal {
        ConstantVal(val)
    }

    ///ConstantValの値を取得する
    pub fn get(&self) -> i32 {
        self.0
    }
}

main.rsも修正。

pub mod calc;

fn main() {
    let a = calc::ast::ConstantVal::new(33);
    println!("ConstantVal={}", a.get());
}

定数のASTのテスト

せっかく、関数を実装したんです。テストも書いてみましょう。Rustのテストはありえないぐらい簡単です。
ast.rsに直接テスト関数を書くだけです！
ast.rsの続きから書いていきましょう。

//impl ConstantVal {..}の下に書く

#[test]
fn constant_val_test() {
    let expect = 55;
    let constant_val = ConstantVal::new(expect);
    assert_eq!(
        constant_val.get(),
        expect
    );
}

#[test]が付けられた関数はテスト実行の時のみコンパイルされ、実行されます。

実際にテストを実行してみましょう。準備するものは何もありません。ただコマンドを１つ打つだけです！

cargo test

ドキュメント自動生成

次に、標準で備わっているドキュメント生成機能を試してみましょう。

cargo doc --no-deps --open

このコマンドでドキュメント生成を自動生成して、ブラウザで開くことができます。

[コマンドの詳細]
https://doc.rust-lang.org/cargo/commands/cargo-doc.html

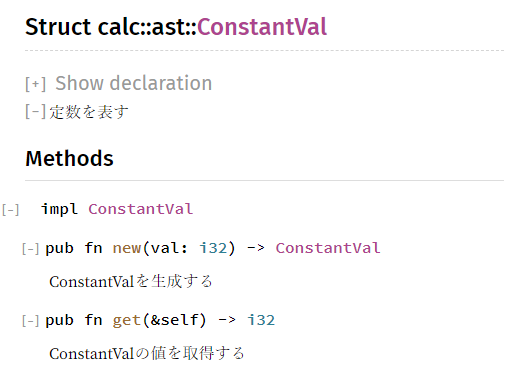
きっとこんな感じになることでしょう。↓

///で書いたコメント文がドキュメントに表示されてますね。
Rustでは//が普通のコメントで///がドキュメント用のコメントになります。

足し算のAST

次に、足し算の式の構造を定義します。

足し算は<任意の式>+<任意の式>という構造になっているはずです。

つまり、足し算の構造は任意の式を二つ持つというわけです。

任意の式についてまだ定義していないのでそちらを定義していきましょう。

任意の式とは、定数、足し算など、さまざまな式のいずれかを取るような構造です。
こういう時はenumを使うと簡単にその構造を定義できます。

他の言語だとenumは単なる識別子として使いますが。
Rustのenumはunion型や直和型と呼ばれる概念に近いものです。

ast.rsの先頭から書く。

///任意の式を表す
pub enum Expr {
    ConstantVal(ConstantVal)
}

///定数を表す
pub struct ConstantVal(i32);
.
.

任意の式の表現が出来たので、足し算の構造を実装していきます。

.
.
#[test]
fn constant_val_test() {...}

///足し算を表す
pub struct PlusOp {
    //演算子の左にある式
    left_expr: Expr,
    //演算子の右にある式
    right_expr: Expr,
}

impl PlusOp {
    ///PlusOpを生成する
    pub fn new(left_expr: Expr, right_expr: Expr) -> PlusOp {
        PlusOp { left_expr, right_expr }
    }
}

次に足し算の式自体も任意の式に含まれるので、ExprにPlusOpを追加します。

///任意の式を表す
pub enum Expr {
    ConstantVal(ConstantVal),
    PlusOp(PlusOp),
}

が、残念ながらこれはコンパイルエラーとなります。
これは、C/C++をやっていれば馴染みが深いエラーかもしれません。
PlusOpの定義自体にExprが含まれるため、循環参照してしまい、サイズがコンパイル時に不定になるからです。

この問題を解決するために、ExprにはPlusOp自身ではなく、PlusOpのポインタを持たせるようにします。
なぜポインタにすると解決するのか。それは、ポインタのサイズは常に一定だからです。

///任意の式を表す
pub enum Expr {
    ConstantVal(ConstantVal),
    PlusOp(Box<PlusOp>),
}

ASTの評価

ではそろそろ、式の計算を実装していきたいと思います。
これからは、式の計算ではなく、式の評価(evaluate)という言葉を使っていきます。

そのために、各種構造(Expr, ConstantVal, PlusOp)にevalという式を評価する関数を定義していきます。

かなり書き換えたので全体のソースコードを載せておきます。

ast.rs

///任意の式を表す
pub enum Expr {
    ConstantVal(ConstantVal),
    PlusOp(Box<PlusOp>),
}

impl Expr {
    ///式を評価する
    pub fn eval(&self) -> i32 {
        match self {
            Expr::ConstantVal(e) => e.eval(),
            Expr::PlusOp(e) => e.eval()
        }
    }
}

///定数を表す
pub struct ConstantVal(i32);

impl ConstantVal {
    ///ConstantValを生成する
    pub fn new(val: i32) -> ConstantVal {
        ConstantVal(val)
    }

    ///定数を評価する
    pub fn eval(&self) -> i32 {
        self.0
    }
}

#[test]
fn constant_val_test() {
    let expect = 55;
    let constant_val = ConstantVal::new(expect);
    assert_eq!(
        constant_val.eval(),
        expect
    );
}

///足し算を表す
pub struct PlusOp {
    //演算子の左にある式
    left_expr: Expr,
    //演算子の右にある式
    right_expr: Expr,
}

impl PlusOp {
    ///PlusOpを生成する
    pub fn new(left_expr: Expr, right_expr: Expr) -> PlusOp {
        PlusOp { left_expr, right_expr }
    }

    ///足し算を評価する
    pub fn eval(&self) -> i32 {
        self.left_expr.eval() + self.right_expr.eval()
    }
}

main.rs

pub mod calc;

fn main() {
    let a = calc::ast::ConstantVal::new(33);
    println!("ConstantVal={}", a.eval());
}

変更点は、
Exprにeval関数を実装し、PlusOpにもeval関数を実装しました。
あとは、ConstantValのget関数をevalにリネームして、統一をしました。

AST評価のテスト

eval関数が新たに定義されたので、テストも追加していきましょう。

.
.
impl PlusOp {
    ...
}

#[test]
fn plus_op_test() {
    //13+(5+1)の足し算式を生成
    let plus_op = PlusOp::new(
        Expr::ConstantVal(ConstantVal::new(13)),
        Expr::PlusOp(
            Box::new(
                PlusOp::new(
                    Expr::ConstantVal(ConstantVal::new(5)),
                    Expr::ConstantVal(ConstantVal::new(1)),
                )
            )
        ),
    );
    let expect = 13 + (5 + 1);
    assert_eq!(
        plus_op.eval(),
        expect
    );
}

簡単のため、テストはPlusOpのみにしました。
また、 Expr::ConstantVal(ConstantVal::new(5))という記述は冗長かもしれませんが、今回はこのスタイルで行きます。

これで、足し算と定数を組み合わせた任意の式を表現でき、評価できようになりました。

四則演算への拡張

ここからは、四則演算ができるように拡張していきましょう。

PlusOpを四則演算全てに対応できるように、改造していきます。

ast.rsのPlusOpをBinaryOpにして修正。

///演算子種別
pub enum OpKind {
    Add,
    Sub,
    Mul,
    Div,
}

///二項演算子を表す
pub struct BinaryOp {
    //適応する演算子種別
    op_kind: OpKind,
    //演算子の左にある式
    left_expr: Expr,
    //演算子の右にある式
    right_expr: Expr,
}

impl BinaryOp {
    ///BinaryOpを生成する
    pub fn new(op_kind: OpKind, left_expr: Expr, right_expr: Expr) 
        -> BinaryOp 
    {
        BinaryOp { op_kind, left_expr, right_expr }
    }

    ///二項演算式を評価する
    pub fn eval(&self) -> i32 {
        let right = self.right_expr.eval();
        let left = self.left_expr.eval();
        match self.op_kind {
            OpKind::Add => left + right,
            OpKind::Sub => left - right,
            OpKind::Mul => left * right,
            OpKind::Div => left / right
        }
    }
}

次にExprも修正していきます。

///任意の式を表す
pub enum Expr {
    ConstantVal(ConstantVal),
    BinaryOp(Box<BinaryOp>),
}

impl Expr {
    ///式を評価する
    pub fn eval(&self) -> i32 {
        match self {
            Expr::ConstantVal(e) => e.eval(),
            Expr::BinaryOp(e) => e.eval()
        }
    }
}
.
.

plus_op_testもbinary_op_testとして書き直します。

.
.
#[test]
fn binary_op_test() {
    //13*(5+1)の式を生成
    let binary_op = BinaryOp::new(
        OpKind::Mul,
        Expr::ConstantVal(ConstantVal::new(13)),
        Expr::BinaryOp(
            Box::new(
                BinaryOp::new(
                    OpKind::Add,
                    Expr::ConstantVal(ConstantVal::new(5)),
                    Expr::ConstantVal(ConstantVal::new(1)),
                )
            )
        ),
    );
    let expect = 13 * (5 + 1);
    assert_eq!(
        binary_op.eval(),
        expect
    );
}

これで、四則演算の数式の構文構造をASTとしてプログラムに落とし込み、評価することができるようになりました！

パーサ実装

パーサについて

ここまでで、四則演算の数式を表現できる構造を定義し終えました。
今や、4+8-2/1や(1-2)*(3+8)などの数式を表現することができます。
ただし、それは自分でプログラムを書いて組み立てていくような面倒なやり方でした。（ちょうどbinary_op_testのような）
そうではなく、"4+7/2+1"などの文字列が与えられたら、それを解析して自動でASTを生成したいと思います。このように、「文字列を解析して構造を組み立てていく関数」のことをパーサと呼びます。

calcフォルダ内にparser.rsというファイルを作ってください。
次にcalc.rsを以下のようにします。

pub mod ast;
pub mod parser;

さて、パーサを実装する前に、先に今回の数式の構文をしっかりとBNFで定義しておきましょう。(BNFの説明については省略します。)

記号のルール
[中身] は中身が「あっても無くても良い」という構文を意味する。
| は「または」を意味する。例えば'a'|'b'で'a'または'b'にマッチする構文。
() は単純に優先順位を明示しているだけ。

<expr>       := <term> [ ('+'|'-') <expr> ]
<term>       := <factor> [ ('*'|'/') <term> ]
<factor>     := <const_val> | <paren_expr>
<paren_expr> := '(' <expr> ')'
<const_val>  := 1つ以上の数字

パーサはある小さな単位の構文を解析し、変換するものです。
今回はBNFに習って、expr, term, factor, paren_expr, const_valという単位でパーサを実装していきます。
パーサはパーサ同士を組み合わせてさらに大きく複雑なパーサを構成することができます。パーサを組み合わせるヘルパ関数のことをパーサコンビネータと呼びます。

パーサとパーサコンビネータを1から自作するのは大変なので、nomというパーサライブラリを使用します。

nomを使ってみよう

[nomのGithub] https://github.com/Geal/nom

[nomのドキュメント] https://docs.rs/nom/5.0.1/nom/

まず、nomの使い方を見ていきましょう。
nomにはいくつかデフォルトで用意されているパーサがあるのでそれを使ってみます。

parser.rsに書いていきます。

use nom::character::complete::digit1;
use nom::IResult;

#[test]
fn digit1_test() {
    let s = "63abc";
    let result: IResult<&str, &str> = digit1(&s);
    let (no_used, used) = result.unwrap();
    assert_eq!("63", used);
    assert_eq!("abc", no_used);
}

digit1は少なくとも1つ以上の数字をパース(パーサを使って解析し変換することをそう言う。)するパーサです。
パーサの返り値はIResult<&str,&str>です。（他の型を指定することも可能ですが）

具体的にはIResult<パースされなかった残りの文字列,パースされたもの>となっています。
パースが成功した場合unwrap()で(残りの文字列,パースされたもの)というタプルを受け取れます。

63はdigit1でパースされますが、abcは数字じゃないのでパースされずに残るわけですね。

定数のパーサ

事前準備が終わったので早速、定数のパーサを書いていきます。

BNFではこう定義していました

<const_val>  := 1つ以上の数字

digit1を使いつつ、定数のパーサを実装したいと思います。

.
.
#[test]
fn digit1_test() {...}

use super::ast::*;

///定数のパーサ
pub fn constant_val_parser(s: &str) -> IResult<&str, ConstantVal> {
    use std::str::FromStr;
    let (no_used, used) = digit1(s)?;
    let val = FromStr::from_str(used).unwrap();
    Ok((no_used, ConstantVal::new(val)))
}

ではconstant_val_parserについて説明していきます。

まず、返り値がIResult<&str,&str>ではなく、IResult<&str, ConstantVal>になっている点に注意してください。
constant_val_parserはパース結果としてConstantValを返したいので、このような型になっています。

2行目では、digit1を使い数字の文字列をパースしています。
IResult型の値の中身を?演算子で取り出して、(no_used, used)という風に変数に格納します。

3行目では、FromStr::from_strを使って、文字列をi32に変換しています。
必ず成功すると仮定してunwrap()で中身を取り出します。
最後にIResultで残りの文字列とパース結果であるConstantValを返します。

---

パーサのルール

パーサ同士を組み合わせて新しいパーサを作れるようにするため、パーサの作成ルールがあります。
それは返り値の型をIResultにすることです。

IResultはResultのエイリアスです。

type IResult<I, O, E = (I, ErrorKind)> = Result<(I, O), Err<E>>;

Iがまだパースされてない残り物の型。

Oがパース結果の型。

Eはパースが失敗した時に返すエラーの型です。

---

定数のパーサをテスト

では、本当に期待通りパーサが実装できているか、テストを書いていきます。

.
.
///定数のパーサ
pub fn constant_val_parser(s: &str) -> IResult<&str, ConstantVal> {...}

#[test]
fn constant_val_parser_test() {
    let (_, actual) = constant_val_parser("889").unwrap();
    let expect = ConstantVal::new(889);
    assert_eq!(actual, expect);
}

動きそうですがこのテストはコンパイルエラーになります。

エラー内容を抜粋するとこんな感じです。

 help: the trait `std::fmt::Debug` is not implemented for `calc::ast::ConstantVal`

要約すると、ConstantValにはDebugのトレイトが無いからだめだよって感じです。
assert_eq!は比較対象にDebug,PartialEqのトレイトを要求します。

ast.rsに定義されているデータ構造をテストをしやすくするため、全てDebug, PartialEqトレイトを持たせたいと思います。
これらのトレイトはコンパイラに自動実装させることが可能なのでそれを使用します。

///任意の式を表す
#[derive(Debug,PartialEq)]
pub enum Expr {...}
.
.

///定数を表す
#[derive(Debug,PartialEq)]
pub struct ConstantVal(i32);
.
.

///演算子種別
#[derive(Debug,PartialEq)]
pub enum OpKind {...}

///二項演算子を表す
#[derive(Debug,PartialEq)]
pub struct BinaryOp {...}
.
.

今度はうまくテストが通ったと思います。

式のパーサ

次に全ての式の組み合わせをパースするパーサを作っていきます。

BNFではこう定義していました。

<expr>       := <term> [ ('+'|'-') <expr> ]

現時点では定数のパーサだけしかないので、とりあえず仮です。

.
.
#[test]
fn digit1_test() {...}

use super::ast::*;

///式のパーサ
pub fn expr_parser(s: &str) -> IResult<&str, Expr> {
    constant_val_parser(s)
        .map(|(no_used, constant_val)|
            (no_used, Expr::ConstantVal(constant_val))
        )
}

///定数のパーサ
.
.

constant_val_parserの返り値がIResult<&str,ConstantVal>で、
expr_parserはその型をmap関数を使ってIResult<&str,Expr>に変換しているだけです。

丸括弧付きの式のパーサ

次は(任意の式)のような丸括弧付きの式のパーサを作っていきます。

BNFではこう定義していました。

<paren_expr> := '(' <expr> ')'

.
.
///式のパーサ
pub fn expr_parser(s: &str) -> IResult<&str, Expr> {...}

use nom::character::complete::char;

///丸括弧で囲まれた式のパーサ
pub fn paren_expr_parser(s: &str) -> IResult<&str, Expr> {
    let (no_used, _) = char('(')(s)?;
    let (no_used, expr) = expr_parser(no_used)?;
    let (no_used, _) = char(')')(no_used)?;
    Ok((no_used, expr))
}

#[test]
fn paren_expr_parser_test() {
    let (_, actual) = paren_expr_parser("(76)").unwrap();
    let expect = Expr::ConstantVal(ConstantVal::new(76));
    assert_eq!(actual, expect);
}

///定数のパーサ
.
.

新しく出てきたcharは指定した1文字をパースするパーサです。

因子のパーサ

次に、定数パーサと丸括弧式パーサを1つのパーサとしてまとめたいと思います。
理由は、この二つの式は優先順位が同じだからです。
これらは一般的に因子(factor)と呼ばれるものなので、factor_parserという名前で作っていきます。

BNFではこう定義していました。

<factor>     := <const_val> | <paren_expr>

.
.
fn digit1_test() {...}

use super::ast::*;
use nom::branch::alt;
use nom::combinator::map;

///式のパーサ
pub fn expr_parser(s: &str) -> IResult<&str, Expr> {
    factor_parser(s)
}

///因子のパーサ
pub fn factor_parser(s: &str) -> IResult<&str, Expr> {
    alt((
        map(
            constant_val_parser, 
            |constant_val| Expr::ConstantVal(constant_val)
        ),
        paren_expr_parser
    ))(s)
}

#[test]
fn factor_parser_test() {
    let (_, actual) = factor_parser("4").unwrap();
    let expect = Expr::ConstantVal(ConstantVal::new(4));
    assert_eq!(actual, expect);

    let (_, actual) = factor_parser("(3)").unwrap();
    let expect = Expr::ConstantVal(ConstantVal::new(3));
    assert_eq!(actual, expect);
}

use nom::character::complete::char;
.
.

今回は新しく、altとmapが出てきました。
altは「または」を表現することができるパーサコンビネータです。
altは複数のパーサを「または」で結合した新しいパーサを作成できます。
どれか一つでもパースが成功したら、そこでストップし、結果を返すような動作をします。
今回は「定数または丸括弧式」を表現するために使ってます。
次にmapですが、これは渡されたパーサのパース結果の値を変換した新たなパーサを生成するパーサコンビネータです。
constant_val_parserパーサのパース結果の型はConstantValなので、整合性を保つためにExpr型に変換してやる必要があるわけです。
後は、expr_parserを修正して定数と丸括弧式をパースできるようにしておきます。

項のパーサ

お次は掛け算、割り算のパーサを作っていきましょう。
掛け算、割り算は優先順位を同じと仮定すると、まとめて一つのパーサとして実装するのが楽です。
これは一般的に項(term)と呼ばれるものなので、term_parserとして実装していきます。

BNFではこう定義していました。

<term>       := <factor> [ ('*'|'/') <term> ]

かなり複雑なので覚悟をしてください。

.
.
///式のパーサ
pub fn expr_parser(s: &str) -> IResult<&str, Expr> {
    term_parser(s)
}

use nom::sequence::tuple;
use nom::combinator::opt;

///項のパーサ
pub fn term_parser(s: &str) -> IResult<&str, Expr> {

    //*/記号をOpKind型にパースするパーサ
    let op_kind_parser =
        map(
            alt((char('*'), char('/'))),
            |op_char|
                match op_char {
                    '*' => OpKind::Mul,
                    '/' => OpKind::Div,
                    _ => panic!("error!")
                },
        );

    //掛け算、割り算のパーサ
    let binary_parser = tuple((
        factor_parser,
        opt(
            tuple((
                op_kind_parser,
                term_parser
            ))
        )
    ));

    //掛け算、割り算のパーサのパースされた値をmapで調整
    map(binary_parser, |(head_expr, tail_expr_opt)| {
        if let Option::Some((op_kind, tail_expr)) = tail_expr_opt {
            Expr::BinaryOp(
                Box::new(
                    BinaryOp::new(op_kind, head_expr, tail_expr)
                )
            )
        } else {
            head_expr
        }
    })(s)
}

#[test]
fn term_parser_test() {
    let (_, actual) = term_parser("4*2/1").unwrap();

    let temp = Expr::BinaryOp(Box::new(
        BinaryOp::new(
            OpKind::Div,
            Expr::ConstantVal(ConstantVal::new(2)),
            Expr::ConstantVal(ConstantVal::new(1)),
        )
    ));
    let expect = Expr::BinaryOp(Box::new(
        BinaryOp::new(
            OpKind::Mul,
            Expr::ConstantVal(ConstantVal::new(4)),
            temp,
        )
    ));
    assert_eq!(actual, expect);
}

///因子のパーサ
.
.

新たに、tupleとoptが出てきました。
これは両方ともパーサコンビネータです。

tupleは複数のパーサを受け取り、それを１つに結合した新たなパーサを生成します。
例えば、

tuple(( 
    char('a'),
    char('b'),
    char('c'),
))

とすれば、abcという文字列をパースするパーサが生成されます。
パース結果の型は(char,char,char)となります。

optは受け取ったパーサから、「無くてもいい、あってもいい」というパーサを生成します。
例えば、

opt(char('h'))

とすれば、hにマッチしてもいいし、マッチしなくても良いというパーサが生成されます。
パース結果の型はOption<char>となります。

式のパーサ再び

最後はexpr_parserに足し算と引き算を実装していきます。
これは、term_parserとほとんど同じような実装になります。

一応BNFも再度置いておきます。

<expr>       := <term> [ ('+'|'-') <expr> ]

///式のパーサ
pub fn expr_parser(s: &str) -> IResult<&str, Expr> {
    //+-記号をOpKind型にパースするパーサ
    let op_kind_parser =
        map(
            alt((char('+'), char('-'))),
            |op_char|
                match op_char {
                    '+' => OpKind::Add,
                    '-' => OpKind::Sub,
                    _ => panic!("error!")
                },
        );

    //足し算、引き算のパーサ
    let binary_parser = tuple((
        term_parser,
        opt(
            tuple((
                op_kind_parser,
                expr_parser
            ))
        )
    ));

    //足し算、引き算のパーサのパースされた値をmapで調整
    map(binary_parser, |(head_expr, tail_expr_opt)| {
        if let Option::Some((op_kind, tail_expr)) = tail_expr_opt {
            Expr::BinaryOp(
                Box::new(
                    BinaryOp::new(op_kind, head_expr, tail_expr)
                )
            )
        } else {
            head_expr
        }
    })(s)
}

これでパーサは完成です。
expr_parserのテストは省略したいと思います。

入出力の実装

便利関数の実装

いよいよ、main.rsに入出力処理を書いて、電卓の入出力インターフェース実装していきたいと思います。
最初に利便性のため、文字列をパースして評価する関数をcalc.rsに実装していきます。

pub mod ast;
pub mod parser;

use nom::Err;
use nom::error::ErrorKind;

///受け取った文字列をパースして評価する
pub fn expr_eval(s: &str) -> Result<i32, Err<(&str, ErrorKind)>> {
    parser::expr_parser(s)
        .map(|(_, expr)| expr.eval())
}

#[test]
fn expr_eval_test() {
    assert_eq!(
        expr_eval("1+2+3+4+5").unwrap(),
        1 + 2 + 3 + 4 + 5
    );

    assert_eq!(
        expr_eval("1+2*3-7").unwrap(),
        1 + 2 * 3 - 7
    );

    assert_eq!(
        expr_eval("(2*24)/(5+3)").unwrap(),
        (2 * 24) / (5 + 3)
    );
}

入出力の実装

では、定義したexpr_evalを用いてmain.rsに入出力を実装していきます。

pub mod calc;

use crate::calc::expr_eval;

fn main() {
    loop {
        let mut s = String::new();
        std::io::stdin().read_line(&mut s).ok();
        match expr_eval(&s) {
            Ok(val) => println!("ok:{}", val),
            _ => println!("構文エラー")
        }
    }
}

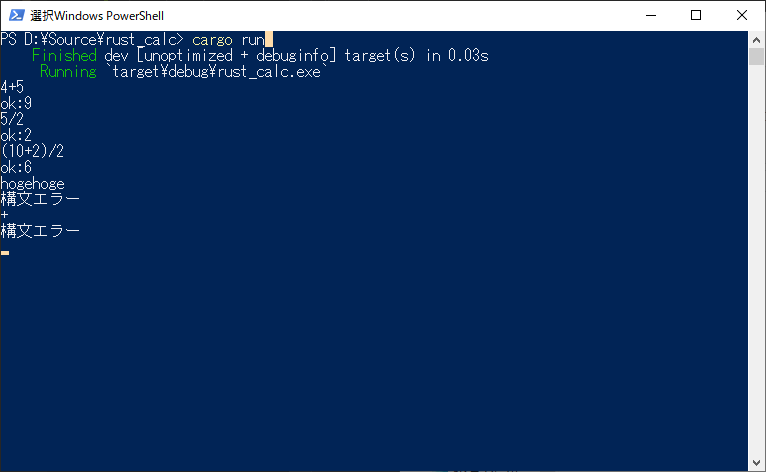
完成です！
cargo runで実行してみましょう。

終わりに

お疲れ様です。

今後の課題

今回の電卓のパーサにはいくつかの課題がまだ残されています。

【4+のような数式が通ってしまう。】

これはnomのeofパーサを使うことで解消できます。

【47　+　3のようにスペースを入れるとエラーになる。】

これはnomのwsパーサコンビネータを使うことで解消できます。

【同じ優先順位の演算子は右から計算されてしまう】

現状の実装では、
例えば1-2-3だと、1-(2-3)のように右から順番に計算されてしまいます。
1-2-3の結果は-4になるべきなのでこれはおかしいですね。
BNFを修正する必要があります。

現状のBNFを見てみましょう。

<expr>       := <term> [ ('+'|'-') <expr> ]

BNFをそのまま解釈すると、右に行けば行くほどASTの木が深くなってしまいます。
プログラムとBNFを修正して改善する必要があるでしょう。