はじめに
この記事は,数列における上極限と下極限について理解したことをまとめた記事です.
Wikipedia( https://ja.wikipedia.org/wiki/上極限と下極限 )を参考にしました.
お願い
間違っている部分がありましたら,コメントで指摘してくださると非常にありがたいです.
そして、説明がわかりにくいという部分があった場合もコメントしてください。
おそらく修正します。
上極限と下極限の概要
実数の数列$(a_n )_{n \in \mathbb{N}}$の上極限(Limit superior)および下極限(Limit inferior)とは,
$n$を無限に大きくしていったときの数列の挙動から決まる実数です。
これは数列の極限に,或る意味でなりうる値を上と下から抑えるために使われています。
$\infty$ と$-\infty$がLimit superiorあるいはLimit inferiorになることを許せば,
数列$(a_n)_{n \in \mathbb{N}}$に極限値がなくても,Limit superior と Limit inferiorは存在します
($\infty, -\infty$が実数でないことに注意します.).
そのため,$(a_n)_{n \in \mathbb{N}}$の極限値が存在しなくとも、
$n$が大きくなったときの数$a_n$がだいたいどのくらいの範囲にあるのかを計算することができます。
上極限(Limit superior)
実数の数列$(a_n)_{n \in \mathbb{N}}$のLimit superiorは以下のように定義されています。
$$
\limsup_{n \to \infty} a_n := \inf_{n\in \mathbb{N}} \sup_{k \geq n} a_k
=\inf \left\{ \sup \left\{ a_k \mid k \geq n \right\} \mid n \in \mathbb{N} \right\}
$$
これだけだと、この式がなにをあらわしているのか想像がつかないよ。Wikipediaさん。。。。
そこで、この式を小さな部品に分解して、
その部品を理解することでこの式全体を理解してみよう。
上式の右辺の中に$\sup \left\{ a_k \mid k\geq n\right\}$という部分があります。
これの$\left\{ a_k \mid k\geq n\right\}$は$(a_n)_{n \in \mathbb{N}}$の$n$番目以上の数の集合$\{a_n, a_{n+1}, \ldots \}$を表しています。
したがって、$\sup \left\{ a_k \mid k\geq n\right\}$は、$(a_n)_{n \in \mathbb{N}}$の$n$番目以上の数の集合$\{a_n, a_{n+1}, \ldots \}$の上限(supremum)ということです。
ここで、
$$
b_n = \sup \left\{ a_k \mid k\geq n\right\}
$$
と書くことにします。
すると、上記の定義は以下のような式に書き直すことができます。
$$
\limsup_{n \to \infty} a_n := \inf_{n\in \mathbb{N}} \sup_{k \geq n} a_k
=\inf \left\{ b_1, b_2, \ldots \right\}
$$
したがって、$(a_n)_{n \in \mathbb{N}}$のlimit superiorは、上記で述べたsupremumの集合$\{ b_1, b_2, \ldots\}$の下限(infimum)ということがわかりました。
下極限(Limit inferior)
実数の数列$(a_n)_{n \in \mathbb{N}}$のLimit inferiorは以下のように定義されています。
$$
\liminf_{n \to \infty} a_n := \sup_{n\in \mathbb{N}} \inf_{k \geq n} a_k
=\sup \left\{ \inf \left\{ a_k \mid k \geq n \right\} \mid n \in \mathbb{N} \right\}
$$
limit superiorのときと同様に、この式を小さな部品に分解して、その部品を理解することでこの式全体を理解してみよう。
上式の右辺の中に$\inf \left\{ a_k \mid k\geq n\right\}$という部分があります。
これの$\left\{ a_k \mid k\geq n\right\}$は$(a_n)_{n \in \mathbb{N}}$の$n$番目以上の数の集合$\{a_n, a_{n+1}, \ldots \}$を表しています。
したがって、$\inf \left\{ a_k \mid k\geq n\right\}$は、$(a_n)_{n \in \mathbb{N}}$の$n$番目以上の数の集合$\{a_n, a_{n+1}, \ldots \}$のinfimumということです。
ここで、
$$
c_n = \inf \left\{ a_k \mid k\geq n\right\}
$$
と書くことにします。
すると、上記の定義は以下のような式に書き直すことができます。
$$
\liminf_{n \to \infty} a_n := \sup_{n\in \mathbb{N}} \inf_{k \geq n} a_k
=\sup \left\{ c_1, c_2, \ldots \right\}
$$
したがって、$(a_n)_{n \in \mathbb{N}}$のlimit inferiorは、上記で述べたinfimumの集合$\{ c_1, c_2, \ldots\}$のsupremumということがわかりました。
まとめ
実数の数列$(a_n)_{n \in \mathbb{N}}$のlimit superior $\limsup_{n \to \infty} a_n$は、
$(a_n)_{n \in \mathbb{N}}$に関するsupremumの集合$\{b_1, b_2, \ldots\}
$のinfimumです。
一方、$(a_n)_{n \in \mathbb{N}}$のlimit inferior $\liminf_{n \to \infty} a_n$は、
$(a_n)_{n \in \mathbb{N}}$に関するinfimumの集合$\{c_1, c_2, \ldots\}
$のsupremumです。
余談
Limit superior とlimit inferiorを求めるプログラムを書きたかったが、
そもそも計算でとけるものなのか?
と、おもっています。
実数の数列$(a_n)_{n \in \mathbb{N}}$のある$m$以上の数$a_m$が
かならず何かの実数より小さいあるいは大きいといった、条件があるときにしか解けないのではないかと考えています。
そこで、limit superiorとlimit inferiorを求めるプログラムの作成は(勝手ながら)断念して、
limit superior やlimit inferiorの定義で説明した、$b_n, c_n$は視覚的にみるとどんな感じになるかを描画してみました。青線が実数の数列$(a_n)_{n \in \mathbb{N}}$、オレンジ線が$\{b_1, b_2, \ldots\}$、緑線が$\{c_1, c_2, \ldots\}$を表しています。
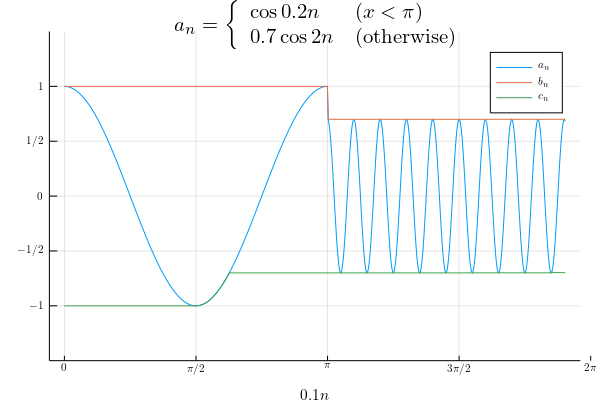
私の勝手なイメージですが、$\{b_1, b_2, \ldots\}$、$\{c_1, c_2, \ldots\}$は
$(a_n)_{n \in \mathbb{N}}$を包む膜だとおもっています。