前回のあらすじ
Tone()関数をつくった。
さて

これは前回の、スケッチのD13の出力です。440Hzが出力されていることが確認できます。
ところで、割り込みの周期はいくつでしょうか
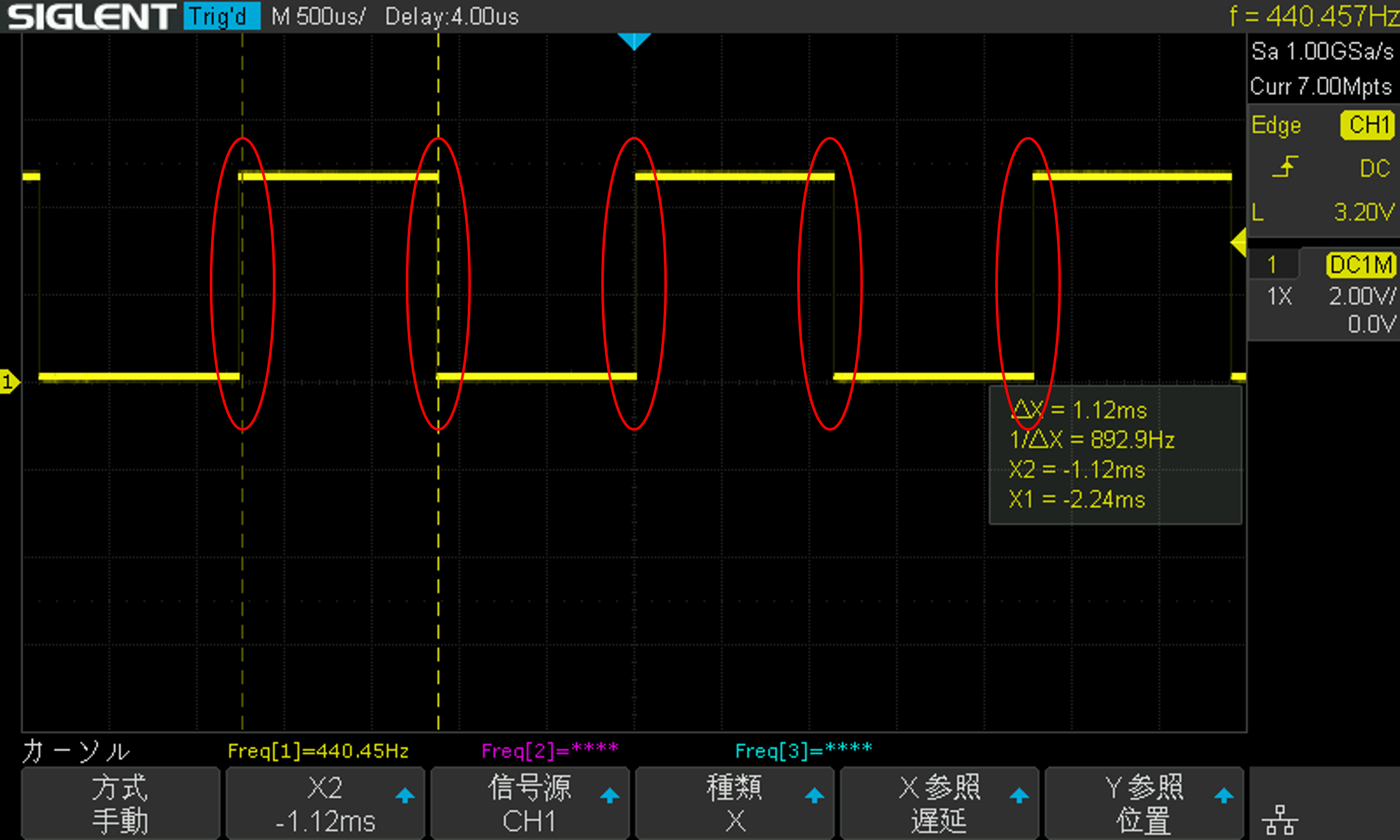
割り込みが発生すると、ピンの状態が変化するので
この赤丸で囲った部分で割り込みが起きています。
つまり、割り込みの周期は2倍の880Hzということになります。
よって、割り込み周期の式は
\begin{align}
f_{interrupt}[Hz]&=\frac{f_{clk_{I/O}}}
{Count\times (OCR2A+1)} \\
\end{align}
となります。
今回のスケッチ
今回使用するスケッチを示します
# define output_pin_A 11
# define output_pin_B 12
# define output_pin_C 13
# define DIV_1 1 //分周無し
# define DIV_8 2 //8分周
# define DIV_32 3 //32分周
# define DIV_64 4 //64分周
# define DIV_128 5 //128分周
# define DIV_256 6 //256分周
# define DIV_1024 7 //1024分周
# define WGM21 0b10 //タイマ2 動作モード設定
# define TOIE2 0b10 //割り込み許可
volatile int operator_A = 0;
volatile int operator_B = 0;
volatile int operator_A_add = 720;
volatile int operator_B_add = 360;
void setup() {
//ピンの設定
pinMode(output_pin_A, OUTPUT);
pinMode(output_pin_B, OUTPUT);
pinMode(output_pin_C, OUTPUT);
//タイマの設定
TCCR2A = WGM21;//CTCモード 比較一致OCR2A
TCCR2B = DIV_8;
OCR2A = 99;//20kHz
TIMSK2 = TOIE2;
sei();//割り込み許可
}
void loop() {
}
ISR(TIMER2_COMPA_vect) {
//割り込み時に実行される関数
digitalWrite(output_pin_C, !digitalRead(output_pin_C));
operator_A += operator_A_add;
operator_A &= 0x7FFF;
operator_B += operator_B_add;
operator_B &= 0x7FFF;
if (operator_A < 0x3FFF) {
digitalWrite(output_pin_A, LOW);
} else {
digitalWrite(output_pin_A, HIGH);
}
if (operator_B < 0x3FFF) {
digitalWrite(output_pin_B, LOW);
} else {
digitalWrite(output_pin_B, HIGH);
}
digitalWrite(output_pin_C, !digitalRead(output_pin_C));
}
このスケッチを書き込むと次のような出力が得られます

volatile とは
volatile int operator_A = 0;
volatile int operator_B = 0;
volatile int operator_A_add = 720;
volatile int operator_B_add = 360;
この、volatileは割り込み処理内で使用する、グローバル変数の型の前に必ずつけます。
これがないと、変数の中身が毎回初期値に戻ってしまいます。
コンパイラの最適化が原因なのでvolatileを付けてコンパイラに最適化させないよう指示をしています。
割り込み周波数
まず、Timer2の割り込みを20kHzに設定しています。
\begin{align}
f_{interrupt}[Hz]&=\frac{f_{clk_{I/O}}}
{Count\times (OCR2A+1)} \\
OCR2A&=\frac{f_{clk_{I/O}}}
{Count\times f_{interrupt}[Hz]} -1\\
OCR2A&=\frac{16 \times 10^6}
{8\times 20 \times 10^3 } -1\\
&=99\\
\end{align}
とうことなので、99になります。
オシロの画像からも、D13から20kHzが出力されていることがわかります。
ISR内
今回も前回と同様にTIMER2_COMPA_vectを使用します。
ISR(XXX){
digitalWrite(output_pin_C, !digitalRead(output_pin_C));
//処理
digitalWrite(output_pin_C, !digitalRead(output_pin_C));
}
D13のピン操作を、割り込み処理内の初めと終わりに入れているのは
処理時間をオシロスコープ等で計測するためです。
割り込み処理に時間がかかると、次の割り込みの時間が来てしまい
loopに戻ることができなくなってしまいます。
また、割り込み処理に時間を取られるとloop内の処理やその他の割り込みに割く時間が無くなってしまいます。
余談
D13にLEDを付けると、負荷率を可視化できます。
アナログメータを付けるのもおすすめです。
DDS ダイレクト・デジタル・シンセサイザー
スケッチ内の
ISR(XXX){
operator_A += operator_A_add;
operator_A &= 0x7FFF;
operator_B += operator_B_add;
operator_B &= 0x7FFF;
}
では、ダイレクト・デジタル・シンセサイザーを実装しています。
名前こそ難しいですが、やっていることは単純で
内部のデジタル値を一定周期で増加させているだけです。
タイマ割り込みでは、分周器と上限値を変えて周波数を変更しました。
DDSでは、上限を決め加算する数を変えて周波数を決定します。
どのようにして、出力周波数が決定されるか追っていきましょう
ISR(XXX){
operator_A += operator_A_add;
operator_A &= 0x7FFF;
}
operator_A がAというオペレータ、位相に当たります。
operator_A_addが加算量、割り込み一回ごとに加算されていきます。
operator_A &= 0x7FFF;
0x7FFFは、16進数表記です。10進数に直すと、

7FFF_{(16)}=32767=2^{15}-1=111 1111 1111 1111_{(2)}
となります。
今回、オペレータには符号ありint型を使用したのでその最大数ですね。
operator_A &= 32767;
であることがわかりましたが、これはいったい何かというと
operator_A = operator_A & 0b111111111111111;
という計算になります。もっとかみ砕くと
operator_A = operator_A % 32767;
と、剰余算になります。
オペレータを加算していくと、いつか桁あふれを起こしマイナスの値になってしまいます。
それを防ぐために、リミット処理を施しています。
剰余算をビット計算に置き換える手法はwikiにも記載があります。
余談
%を使った処理は、遅いです。試しに、&=を%=にしてみてください。
処理が間に合わなくなり、出力周波数が落ちるはずです。
出力周波数を得るための加算量の計算方法
ここから、厄介で自分もよく計算方法を忘れてしまいます。
のこぎり波を作り、一定の大きさを超えたらHIGHに、下回ったらLOWにしています。
まず、オペレータが0から加算していき何回目でオーバーフローするか計算します
\begin{align}
OVF_{count}&=\frac{32767}
{Add} \\
\end{align}
つまり、上限数を加算量で割ればいいことになります。
今回の場合
\begin{align}
OVF_{count}&=\frac{32767}
{Add} \\
OVF_{count}&=\frac{32767}
{720} \\
&=45.5\\
\end{align}
と、おおよそ46回でオーバーすることがわかりました。
オーバーフローする回数がわかったということは、オーバーフローするまでの時間もわかります。
\begin{align}
OVF_{time}&=t_{sample}\times OVF_{count}\\
OVF_{time}&=\frac{1}
{f_{sample}} \times OVF_{count}\\
\end{align}
加算する時間は、割り込み周期なのでサンプリング時間をかけてあげればいいだけです
\begin{align}
OVF_{time}&=t_{sample}\times OVF_{count}\\
OVF_{time}&=\frac{1}
{10^{10^3}} \times 45.5\\
&=0.002275\\
\end{align}
0.002275秒でオーバーフローすることがわかりました。
さて、肝心の周波数は
f[Hz]={OVF_{time}}^{-1}=1 \div OVF_{time} = 1\div 0.002275=439.56Hz
ようやく、440Hzが出ることがわかりました。
ここまでの式を整理しましょう。
\begin{align}
f_{output}&=\frac{1}{OVF_{time}}\\
&=\frac{1}{\frac{1}
{f_{sample}} \times OVF_{count}}\\
&=\frac{f_{sample}}{OVF_{count}}\\
&=\frac{f_{sample}}{\frac{32767}
{Add}}\\
&=\frac{f_{sample} \times Add}{32767}\\
\end{align}
となります。検算をしてみましょう。
\begin{align}
f_{output}&=\frac{f_{sample} \times Add}{32767}\\
&=\frac{20 \times 10^3 \times 720}{32767}\\
&=439.4Hz
\end{align}
無事合っていましたね。
さてさて、Addが決まっていることは通常あり得ませんね。
任意の出力周波数の時の式に変形しましょう。
\begin{align}
f_{output}&=\frac{f_{sample} \times Add}{32767}\\
f_{output}\times \frac{1}{Add}&=\frac{f_{sample} \times Add}{32767}\times \frac{1}{Add}\\
f_{output}\times \frac{1}{Add}&=\frac{f_{sample}}{32767}\\
f_{output}\times \frac{1}{Add} \times \frac{1}{f_{output}}&=\frac{f_{sample}}{32767} \times \frac{1}{f_{output}}\\
\frac{1}{Add} &=\frac{f_{sample}}{32767} \times \frac{1}{f_{output}}\\
\frac{1}{Add} &=\frac{f_{sample}}{32767 \times f_{output}} \\
{Add} &=\frac{32767 \times f_{output}}{f_{sample}} \\
\end{align}
となります。
検算しましょ~
\begin{align}
{Add} &=\frac{32767 \times f_{output}}{f_{sample}} \\
&=\frac{32767 \times 440}{20 \times 10^3} \\
&= 720.874
\end{align}
合ってますね。
まとめ
これでようやく、DDSの説明が終わりました。
出力される周波数を、変えたいときは割り込み周期を変えるか、加算値を変えればいいことがわかっていただけたでしょうか。
これさえ、理解できればマイコンだろうがFPGAだろうがなにが来てもすぐにシンセサイザーにすることができます。(たぶん)
この式大事
\begin{align}
{Add} &=\frac{32767 \times f_{output}}{f_{sample}} \\
\end{align}
ISR(XXX){
operator_A += operator_A_add;
operator_A &= 0x7FFF;
operator_B += operator_B_add;
operator_B &= 0x7FFF;
}
このオペレータの数を増やせばそれだけ多くの周波数を出力することができます。
今回は、D12,D11の2つでしたがArduinoにはまだまだピンがあります。
処理時間の関係で無限には難しいですが。10音くらいは出せると思います。
試してみてください。
次回
今回は、確かに和音ではありますが
その音の数だけスピーカーないしは、ミキサーが必要ですね。
次回はそこを何とかしようと思います。
おわりに
長文をよんでくださりありがとうございました。
6000文字も書いてしまったみたいです。気を付けます。
