この記事はNorth Detail Advent Calendar 2019の20日目の記事です
前書き
AtCoderがUnlambdaに対応している, という話を以前耳にしました.
今までUnlambdaはなんとなくやり口が卑怯な気がして避けていたのですが,
その(恐らく)誤解を解消する良い機会だと思ってUnlambdaでAtCoderに挑戦してみた, という話です.
Unlambda
Unlambdaは11種(11種とは言っていない)のプリミティブ関数と関数適用演算子から成る(難解)関数型プログラミング言語です.
言語仕様についてはこことかここ(英語・公式)とかが詳しいです.
もしこの記事を理解して読もうとしてくれている(しかしUnlambdaは初めてな)奇特な方がいらっしゃれば, 日本語解説ページの「基本的な組み込み関数」の項を事前に読んでおいていただければと思います.
Hello, World!を出力するプログラムは以下のように書けます.
`````````````.H.e.l.l.o.,. .W.o.r.l.d.!i
あれ, 簡単だな!?
公式ページ曰く
Writing Unlambda programs isn't really as hard as it might seem; however, reading Unlambda programs is practically impossible.
Unlambdaでのプログラミングは見た目ほどには難しくない, しかしUnlambdaのプログラムを読解することは実質的に不可能だ.
とのことですし, 体験した身としてはこの文にはかなり同意できます.
少なくともGrassよりは遥かに書きやすいので
難解プログラミング言語に触ってみたいけどどれにするか悩んでいるなんて人にはオススメです.
挑戦するお題
加算王という問題に挑戦します.
標準入力から(十進数の)2桁の数字を受け取り, 十の位と一の位の和を(十進数で)出力するという問題です.
入力例1
23
出力例1
5
入力例2
99
出力例2
18
回答へのアプローチ
この問題は以下の3つの部分問題から構成されています.
- 標準入力から数字を読み込む
- 和を計算する
- 標準出力に和を書き出す
一見簡単に見えますが, 流石は天下のAtCoder, どの部分問題にも一筋縄ではいかない難所を用意しています.
まずは読み込みの部分, 入力されるのは当然数値ではなくただの文字(数字)であるため, '0' ~ '9'の数字を0 ~ 9の数値に変換しなければ, 次の和の計算に入ることができません.
次に和を計算する部分, みなさんも幼少の頃につまづいたことがあるかもしれませんが, 足し算には「繰り上がり」の概念が存在します. 5 + 6の和にただ1文字で対応する数字は十進数には存在せず, 繰り上がりの考え方を使い2文字で11と表さなくてはいけません. 結果から言うと, この問題が十九進数(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f, g, h, i)による出力を許容していたならもう少し簡単に解くことができたのですが, それを許さないAtCoderはやはり参加者に対し妥協無しの高いプログラミングスキルを要求している, と言うことなのだと思います.
最後に書き出しの部分, 先に述べた難所とも関連があるのですが, 出力を十進数のただ一つの文字で表せる場合(4など)は0埋めせずにただ一文字'4'と出力しなければならないことです.
出力は最大で二文字なのだから, 一貫させて'04'でもいいだろうという甘えは一蹴されます.
また, 当然数値の4を数字の'4'に変換する必要もあります. <EOT>を出力しても正解とはみなされません.
これらの難所を考慮すると, この問題の回答となるようなプログラムには以下のような流れが求められます.
かなり長くて先が思いやられますが, 1つずつ片付けていきましょう.
Unlambdaにおける数値の扱い
と, その前にUnlambdaにおける数値の取り扱いについて説明する必要があります.
Unlambdaの世界にはint型とかNumber型というのは存在しません. というか, function型しか存在しません. そう, なんか頑張って関数で数値を表現する必要があるということです.
この課題に対する回答の一つとして, チャーチ数(Church encoding)が知られており, 本記事でもこれを採用します.
チャーチ数<n>は引数fを受け取り, 「引数xを受け取り, f(....f(f(x))を返す関数」を返します. fを繰り返し適用する回数はn回です.
具体例を挙げるとチャーチ数<4>は引数fを受け取り, 「引数xを受け取り, f(f(f(f(x))を返す関数」を返します.
本記事では今後チャーチ数を表す表記として<0> ~ <9>を使用します.
出力機能の実装
順番がおかしいのではないかと思われるかもしれませんが, Unlambdaでのプログラミングでは一回途中結果を出力して確認したいというシーンがしばしば出てきます.
今後の作業を円滑にするためにも出力機能を最初に作ってしまうのが妥当だと判断しました.
まずUnlambdaでの出力について簡単に説明をします. Unlambdaでは.Xという関数を使って出力を行います. Xには任意の文字が入ります. 例えば.Aという関数は, 任意の引数を受け取って, 'A'を出力し, 引数をそのまま返す関数です. また, 関数適用には`演算子を使います. `AB はBを引数としてAを呼び出すという意味です.
要するに, `.H.eというプログラムは.eを引数として.Hを呼び出すと言うことを表しており, その結果標準出力には'H'が書き出され, 関数呼び出しの結果は.eとなります(.Hは引数をそのまま返す関数であることを思い出してください).
これを踏まえると, 最初のHello, World!が読めてきます. .H, .e, .l... が順番に呼び出されていく仕組みになっています.
さて, 今回はこれを少し発展させて, 「数値を受け取ってその数値に対応する数字を出力する関数」<print>を実装します. みんな大好きPython3で書くとこんな関数です.
def _print(n):
print(str(n), end='')
str入れなくても動くじゃん!(ありがたい話ですよね)
Unlamdaにはlexical castを行なってくれるプリミティブ関数は存在しないため, 自前でなんとかする必要があります.
作戦はこうです.
-
[.0, .1, .2, .3, .4, .5, .6, .7, .8, .9]というリスト<nlist>を作る. -
<print>は数値nを受け取り,<nlist>のn番目の要素をプリミティブ関数iを引数として呼び出す(iである必要はなく実際はなんでも良い).
Unlambdaにはリストを作ってくれるプリミティブ関数が存在しないため, 自前でなんとかする必要があります.
そのため, 公式ページでも紹介されている, 順序対(cons)を使う方法を採用します. 順序対はPython的に言うと大きさ2のタプルです.
順序対の左の値をリストの値, 右の値を残りのリストとすることでリストを表現します.
Python的に書くと以下のような感じです.
(0, (1, (2, (3, (4, (5, (6, (7, (8, (9, None))))))))))
こうしておくと, i(iは0から始まる / これはプリミティブ関数のiではない)番目の要素はi回右の要素を参照し, その後左の要素を参照することで取得できるという, どこからどうみてもリストな動きが得られます.
consの書き方
Unlambdaには順序対を作ってくれるプリミティブ関数が存在しないため, 自前でなんとかする必要があります.
その方法は公式ページに書いてあるので有り難く使わせてもらいます.
consは日本語で言うと, 引数uとvを取り, 「引数fを受け取りf(u)(v)を返す関数」を返す関数と表現できます.
公式ページで使われるラムダ式ライクな書き方をすると
^u^v^f``$f$u$v
Unlambda的に書くと
``s``s`ks``s`kk``s`ks``s`k`sik`kk
Python的に書くと
def cons(u):
def cons1(v):
def cons2(f):
return f(u)(v)
return cons2
return cons1
Unlambdaのやつどうやって書いたんだよ!は当然のツッコミです. これは上記のラムダ式ライクな書き方から機械的な変換により導出することができます.
実際のところ, 感覚さえつかめればラムダ式ライクな書き方は意外とやれるものです. Unlambdaのプログラミングとは即ち, ラムダ式ライクな書き方で関数を書き, 機械的変換を用いてUnlambdaのコードに落とし込む作業とも言うことができます. 変換の方法は少し長いので興味がある方は公式ページを参照してください.
car, cdrの書き方
<cons>から左の値を取り出すための<car>, 右の値を取り出すための<cdr>は以下のように書くことができます.
順序対$pに対し, `<car>$p, `<cdr>$pのように使います.
ラムダ式ライクスタイル(上: car, 下: cdr)
^p`$pk
^p`$p`ki
Unlambda(上: car, 下: cdr)
``si`kk
``si`k`ki
Python
def k(x):
def k1(f):
return x
return k1
def i(f):
return f
def car(p):
return p(k)
def cdr(p):
return p(k(i))
p = cons(1)(2)
print(car(p), cdr(p)) # 1 2
atの書き方
ここまでくると, <cons>で作った擬似リストのi番目の要素を取り出す<at>も作れるようになります. リストlとチャーチ数<n>を受け取り, lにn回<cdr>を適用し, その結果に<car>を適用します.
lにn回を適用すると言う部分は, まさにチャーチ数の力が発揮される部分です. `$n<cdr>とするだけで, 引数に対し<cdr>をn回適用する関数を作り出すことができます.
ラムダ式ライクスタイル
^l^n`<car>``$n<cdr>$l
Unlambda
``s`k`s`k``si`kk``s`k`s``si`k``si`k`kik
Python
def v(f):
return v
def at(l, n):
for i in range(n):
l = cdr(l)
return car(l)
l = cons(0)(cons(1)(cons(2)(v)))
print(at(l, 2)) # 2
nlistの書き方
.0 ~ .9を保持するリストはこうです
ラムダ式ライクスタイル
`^p``$p.0``$p.1``$p.2``$p.3``$p.4``$p.5``$p.6``$p.7``$p.8``$p.9v<cons>
Unlambda
```s``si`k.0``s``si`k.1``s``si`k.2``s``si`k.3``s``si`k.4``s``si`k.5``s``si`k.6``s``si`k.7``s``si`k.8``s``si`k.9`kv``s``s`ks``s`kk``s`ks``s`k`sik`kk
Python
nlist = cons(0)(cons(1)(cons(2)(cons(3)(cons(4)(cons(5)(cons(6)(cons(7)(cons(8)(cons(9)(v))))))))))
printの書き方
これでようやく<print>を書く段階に入れます.
ラムダ式ライクスタイル
^n```<at><nlist>$ni
Unlambda
``s```s`k`s`k``si`kk``s`k`s``si`k``si`k`kik```s``si`k.0``s``si`k.1``s``si`k.2``s``si`k.3``s``si`k.4``s``si`k.5``s``si`k.6``s``si`k.7``s``si`k.8``s``si`k.9`kv``s``s`ks``s`kk``s`ks``s`k`sik`kk`ki
Python
def _print(n):
print(at(nlist, n), end='')
_print(4) # 4
第1部完
入力機能の実装
Unlambdaで標準入力から読み込むのにはこれまた一癖あります.
@関数は引数Xを受け取り, 標準入力から一文字読み込み, <current_character>なる専用の記憶領域に保存します.
その後, 読み込みに成功していたらXにiを, EOFならvを渡します.
<current_character>がXに渡されるわけではないのです. カナシイ.
?X関数は 引数Yを受け取り, <current_character>がXならiを, X以外ならvをYに渡します. Xは任意の文字です. ?Aも?zもあります.
つまり@で1文字読み込んだ後に?X関数を使って一文字一文字コレジャナイコレジャナイと見比べていく必要があります.
pythonで書くとこんなイメージです.
current_character = None
def atmark(X):
global current_character
import sys
current_character = sys.stdin.read(1)
if len(current_character) >= 1:
return X(i)
else:
return X(v)
def check(X, Y):
if X == current_character:
return Y(i)
else:
return Y(v)
getcの書き方
?Xを駆使して, <current_character>に対応する<0> ~ <9>を返す関数<getc>を書くことができます.
`@<getc>
とすることで, 一文字読み込んでそれに対応するチャーチ数が返されると言う寸法です.
プリミティブ関数cの動きをPythonで書くのが難しかったためPython版は無しです. すみません...
ラムダ式ライクスタイルのイメージとしては, 連なる()それぞれの内部で一文字ずつ比較していって, 合致した瞬間に対応するチャーチ数をreturnする感じです.
ラムダ式ライクスタイル
`d^a`$a`c^q`````````(`?0^b``$b$q<0>)(`?1^b``$b$q<1>)(`?2^b``$b$q<2>)(`?3^b``$b$q<3>)(`?4^b``$b$q<4>)(`?5^b``$b$q<5>)(`?6^b``$b$q<6>)(`?7^b``$b$q<7>)(`?8^b``$b$q<8>)(`?9^b``$b$q<9>)
Unlambda
`d``si`k`c``s``s``s``s``s``s``s``s``s``s`k?0``s``s`ks``s`k`sik`k`k`ki``s`k?1``s``s`ks``s`k`sik`k`ki``s`k?2``s``s`ks``s`k`sik`k`k``s``s`kski``s`k?3``s``s`ks``s`k`sik`k`k``s``s`ksk``s``s`kski``s`k?4``s``s`ks``s`k`sik`k`k```s``s`kski``s``s`kski``s`k?5``s``s`ks``s`k`sik`k`k``s``s`ksk```s``s`kski``s``s`kski``s`k?6``s``s`ks``s`k`sik`k`k````s`ksk``s``s`kski``s``s`ksk``s``s`kski``s`k?7``s``s`ks``s`k`sik`k`k``s``s`ksk````s`ksk``s``s`kski``s``s`ksk``s``s`kski``s`k?8``s``s`ks``s`k`sik`k`k```s``s`ksk``s``s`kski``s``s`kski``s`k?9``s``s`ks``s`k`sik`k`k```s``s`kski``s``s`ksk``s``s`kski
getsの書き方
今回の問題「加算王」では入力は二文字のため, 一度getcを呼び出すだけでは不十分です. ということで, getcを拡張して標準入力から複数の文字を受け取り対応する数値のリストを返す<gets>を考えます. '42'が入力されたら, (4 (2 v))を返すイメージです. 再帰によるループを使っています. このテクニックについては公式ページに載っています.
ラムダ式ライクスタイル
```sii^h`@^a```$a<cons>`<getc>$a``$a$h$h
Unlambda
```sii``s`k@``s`k`s``s``si`k``s``s`ks``s`kk``s`ks``s`k`sik`kk`d``si`k`c``s``s``s``s``s``s``s``s``s``s`k?0``s``s`ks``s`k`sik`k`k`ki``s`k?1``s``s`ks``s`k`sik`k`ki``s`k?2``s``s`ks``s`k`sik`k`k``s``s`kski``s`k?3``s``s`ks``s`k`sik`k`k``s``s`ksk``s``s`kski``s`k?4``s``s`ks``s`k`sik`k`k```s``s`kski``s``s`kski``s`k?5``s``s`ks``s`k`sik`k`k``s``s`ksk```s``s`kski``s``s`kski``s`k?6``s``s`ks``s`k`sik`k`k````s`ksk``s``s`kski``s``s`ksk``s``s`kski``s`k?7``s``s`ks``s`k`sik`k`k``s``s`ksk````s`ksk``s``s`kski``s``s`ksk``s``s`kski``s`k?8``s``s`ks``s`k`sik`k`k```s``s`ksk``s``s`kski``s``s`kski``s`k?9``s``s`ks``s`k`sik`k`k```s``s`kski``s``s`ksk``s``s`kski``s``s`ks``s`k`sikk
第2部完
足し算の実装
最後に足し算を実装します. ただの足し算だけではなく, 先に作った出力機能(<0> ~ <9>しか出力できない)に対応するために, 一の位と十の位に分ける機能も必要になります.
一つずつやっていきましょう.
チャーチ数界隈では足し算n+mは「mの次の数をn回求める」というプロセスで計算することがあるらしいです. 今回はこの作戦でいきます.
次の数を求める関数<succ>さえ作ってしまえば, <succ>をn回適用するなんてチャーチ数の最も得意とする分野のため後は楽勝です. さあ<succ>を作りましょう!
succの書き方
単純に, n回適用した後さらにもう一回適用するというアプローチをとります.
ラムダ式ライクスタイル
^n^f^x`$f``$n$f$x
Unlambda
`s``s`ksk
addの書き方
ラムダ式ライクスタイル
^n^m``$n<succ>$m
Unlambda
``si`k`s``s`ksk
upper_digitの書き方
次に, nの十の位を求める<upper_digit>を作ります. これを作るためには公式ページにある<ifthenelse>: ^b`c^q``k`ki``$b$qk -> ``s`kc``s`k`s`k`k`ki``ss`k`kkと<leq>: ``s``s`ks``s`kk``s``si`k``s`k`sik`k`ki`k``s``si`k``s`k`sikvが必要なため, ここにも載せておきます.
<ifthenelse>は3引数を取り, 第一引数がiなら第二引数を, vなら第三引数を返す関数です. <leq>(less than or equal)は2引数を取り, 第一引数が第二引数以下ならi, それ以外はvを返す関数です.
「加算王」で発生する足し算の値域は[0 18]のため, <upper_digit>は引数が<9>以下なら<0>, それ以外なら<1>を返す関数として実装して問題ありません.
それを踏まえて<upper_digit>は以下のように実装できます.
ラムダ式ライクスタイル
^n```<ifthenelse>``<leq>$n<9><0><1>
Unlambda
``s``s``s`k``s`kc``s`k`s`k`k`ki``ss`k`kk``s``s``s`ks``s`kk``s``si`k``s`k`sik`k`ki`k``s``si`k``s`k`sikv`k```s``s`kski``s``s`ksk``s``s`kski`k`ki`ki
lower_digitの書き方
nの一の位を求める<lower_digit>は少々厄介です. 実質的な剰余演算を実装することになります(n mod 10を求めるイメージ). これは以下のような考え方で作ることができます.
- 引数が
<8>以下なら引数の次の数,<9>以上なら<0>を返す関数<rot10>を作ります. -
<0>に対して<rot10>をn回適用します.
<rot10>の書き方は<upper_digit>と似ていますね. こんな感じになります.
ラムダ式ライクスタイル
^n```<if>``<leq>$n<8>`<succ>$n<0>
Unlambda
``s``s``s`k``s`kc``s`k`s`k`k`ki``ss`k`kk``s``s``s`ks``s`kk``s``si`k``s`k`sik`k`ki`k``s``si`k``s`k`sikv`k```s``s`ksk``s``s`kski``s``s`kski`s``s`ksk`k`ki
そしてこの<rot10>を使って<lower_digit>を作ります.
ラムダ式ライクスタイル
^n``$n<inc_rot10><0>
Unlambda
``s``si`k``s``s``s`k``s`kc``s`k`s`k`k`ki``ss`k`kk``s``s``s`ks``s`kk``s``si`k``s`k`sik`k`ki`k``s``si`k``s`k`sikv`k```s``s`ksk``s``s`kski``s``s`kski`s``s`ksk`k`ki`k`ki
勝ったッ!第3部完!
パーツを組み上げる
入力・足し算・出力と必要なパーツは揃いました. あとはこれを組み上げることで「加算王」となることができます. 緊張してきた.
処理は右から左に流れていきます. まず<gets>で入力の数字に対応するチャーチ数のリストを取得, すぐ左の()ではリストの第一要素と第二要素の足し算を行います.
次の()では和の十の位の値を求め, その値の回数(0回か1回)だけ'1'を出力する関数を作り出し, 和の一の位の値を引数として呼び出します. その返り値は当然和の一の位の値なので, その値を<print>に渡します. 最後に改行を出力して終わりです.
ラムダ式ライクスタイル
`r`<print>`(^n```<upper_digit>$n.1`<lower_digit>$n)`(^p``<add>`<car>$p`<car>`<cdr>$p)<gets>
Unlambda
`r```s```s`k`s`k``si`kk``s`k`s``si`k``si`k`kik```s``si`k.0``s``si`k.1``s``si`k.2``s``si`k.3``s``si`k.4``s``si`k.5``s``si`k.6``s``si`k.7``s``si`k.8``s``si`k.9`kv``s``s`ks``s`kk``s`ks``s`k`sik`kk`ki```s``s``s``s``s`k``s`kc``s`k`s`k`k`ki``ss`k`kk``s``s``s`ks``s`kk``s``si`k``s`k`sik`k`ki`k``s``si`k``s`k`sikv`k```s``s`kski``s``s`ksk``s``s`kski`k`ki`ki`k.1``s``si`k``s``s``s`k``s`kc``s`k`s`k`k`ki``ss`k`kk``s``s``s`ks``s`kk``s``si`k``s`k`sik`k`ki`k``s``si`k``s`k`sikv`k```s``s`ksk``s``s`kski``s``s`kski`s``s`ksk`k`ki`k`ki```s``s`k``si`k`s``s`ksk``si`kk``s`k``si`kk``si`k`ki```sii``s`k@``s`k`s``s``si`k``s``s`ks``s`kk``s`ks``s`k`sik`kk`d``si`k`c``s``s``s``s``s``s``s``s``s``s`k?0``s``s`ks``s`k`sik`k`k`ki``s`k?1``s``s`ks``s`k`sik`k`ki``s`k?2``s``s`ks``s`k`sik`k`k``s``s`kski``s`k?3``s``s`ks``s`k`sik`k`k``s``s`ksk``s``s`kski``s`k?4``s``s`ks``s`k`sik`k`k```s``s`kski``s``s`kski``s`k?5``s``s`ks``s`k`sik`k`k``s``s`ksk```s``s`kski``s``s`kski``s`k?6``s``s`ks``s`k`sik`k`k````s`ksk``s``s`kski``s``s`ksk``s``s`kski``s`k?7``s``s`ks``s`k`sik`k`k``s``s`ksk````s`ksk``s``s`kski``s``s`ksk``s``s`kski``s`k?8``s``s`ks``s`k`sik`k`k```s``s`ksk``s``s`kski``s``s`kski``s`k?9``s``s`ks``s`k`sik`k`k```s``s`kski``s``s`ksk``s``s`kski``s``s`ks``s`k`sikk
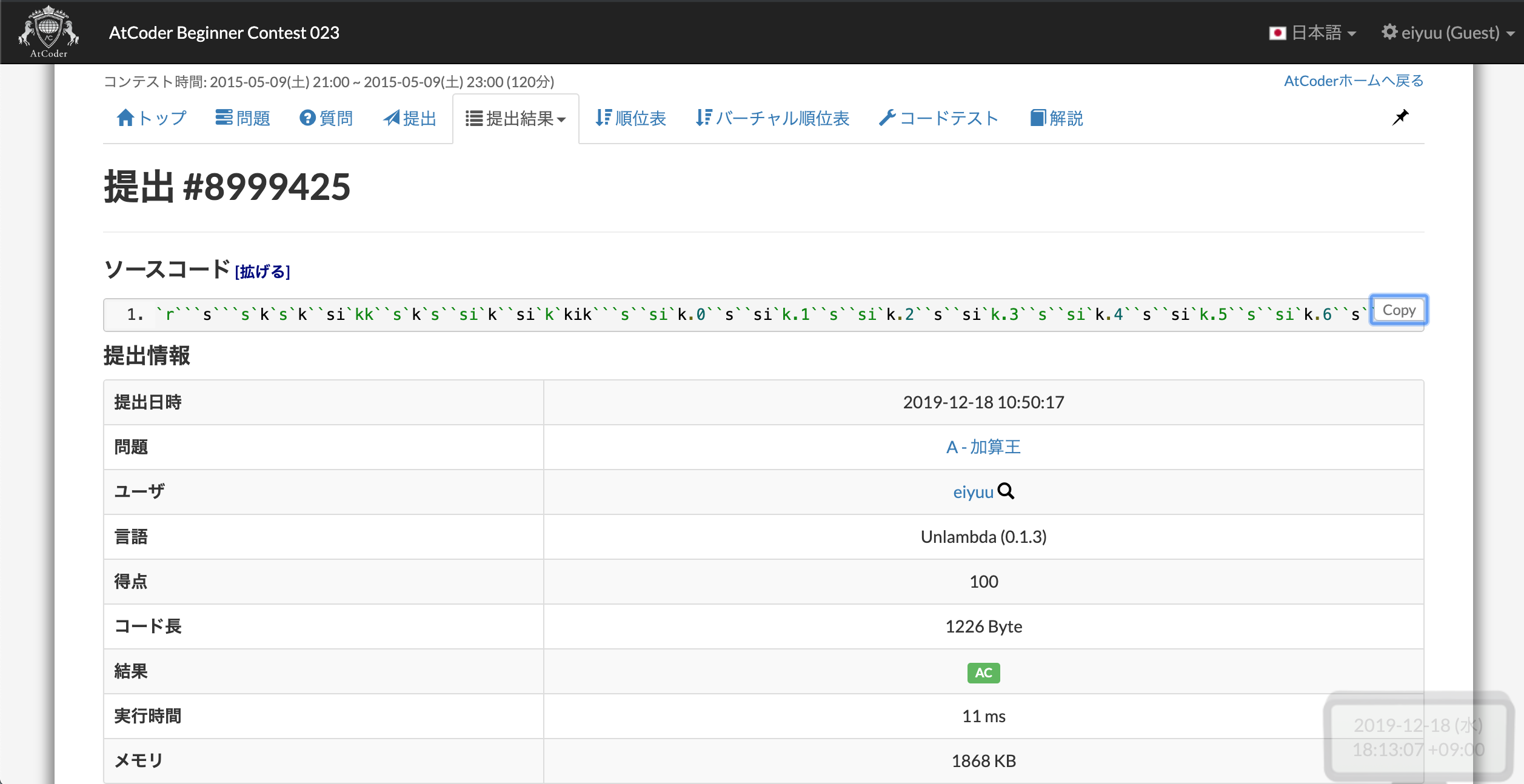 ヤッタネ!
ヤッタネ!
まとめ
本記事ではUnlambdaでAtCoderの過去問「加算王」に挑戦した話を書きました.
「加算王」の処理を部分問題に分解し, 各部分においてUnlambdaで実装する理論について説明を行い, 対応するUnlambdaプログラムを作成しました.
そして, それらを組み合わせることにより「加算王」の正答となるUnlambdaプログラムを作成しました.
お世話になったサイト
Unlambdaが動くWebアプリケーション
Unlambda Interpreter
North Detail会社ブログに転載しています