スプレッドシートで微分擬き

はじめに

慣れ親しんだ表計算ソフトだけで微分がしたい。これから紹介するのは、そんな思いを抱える一人のノンプログラマが、小一時間で編み出した泥臭い力技である。導関数を求めることは無理でも、微分係数に当たりを付けることは可能だと気が付いたのだ。解説に入る前に、計算の流れを説明する。

計算の流れ

関数f(x)について、

1. 変数xを適当な値aと置く。
2. 普通にf(a)を計算する。
3. daをaに比例した微小な値a*10^-10などと置く。
4. f(a+da)を計算する。
5. 項目2,3,4を使って、(f(a+da)-f(a))/daを計算する。

以上。何をやっているかというと、微分の定義そのものから、極限の計算を省いた、言わば微分擬き。単純だが、いざ表計算ソフトでやろうとすると躓きうるので、以下に詳細を解説する。

詳細

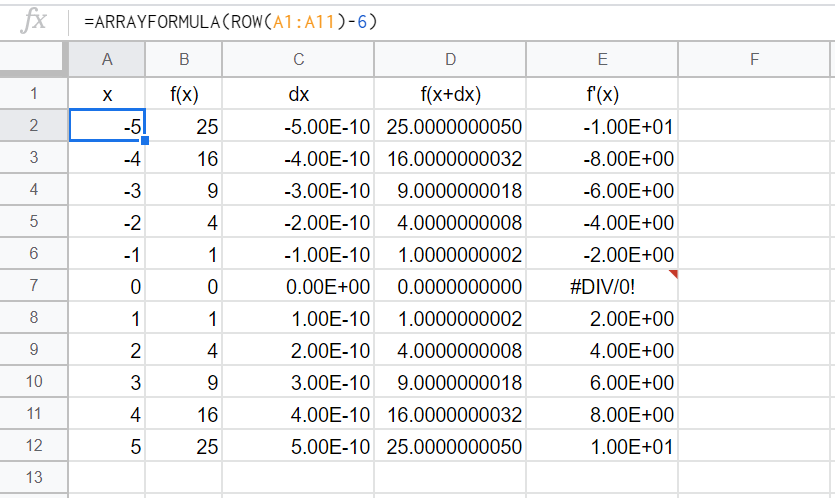
今回は、適当にx=0,±1,±2,±3,±4,±5とする。

A2

=ARRAYFORMULA(ROW(A1:A11)-6)

ARRAYFORMULA()は、Googleスプレッドシート独自の関数なので、Excel派の人は、引数を単一のセルにしてオートフィル。ROW()についても、リンクを参照。

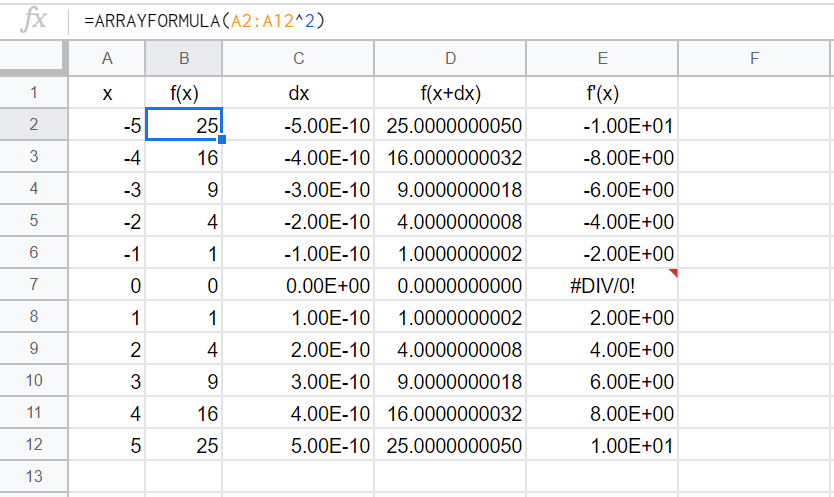
次に、f(x)だが、今回は簡単のためx^2とする。

B2

=ARRAYFORMULA(A2:A12^2)

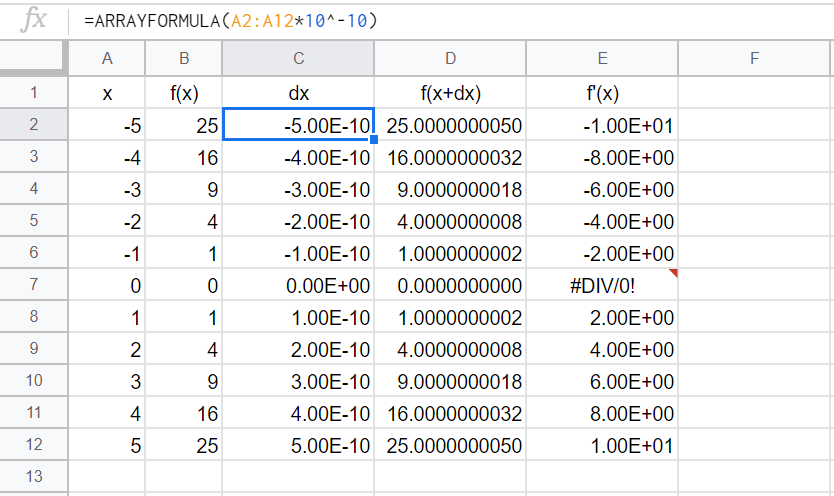
次のdxは、限りなく0に近い値にしたいが、それはあくまで「xと比較したときに」という前提のもとである。今回は、適当にdx=x*10^-10とした。微分係数の必要な桁数に応じて、調整いただきたい。

C2

=ARRAYFORMULA(A2:A12*10^-10)

さて、次のf(x+dx)は、入力方法にポイントがある。今回は、x^2というシンプルな関数だから、問題ないかもしれない。しかし、これが複雑な多項式になったとき、数式の入力がかなり面倒になる。プログラミングの原則に、DRY(Don't repeat yourself)なるものがあるらしいが、これはスプレッドシートにおいても同じことだと思う。

具体的な話に戻ろう。D2セルには、f(x+dx)に当たる数式をそのまま打ち込むのではなく、B2セルから数式をコピペして、変数だけを置換してほしい。手順の例を書くと以下のようになる。

• B2セルを編集可能にする。
• 数式を全選択してコピー。エンターキーで編集を解除。
• D2セルを編集可能にする。
• 数式の貼り付け。エンターキーで編集を解除。
• D2セルを選択。
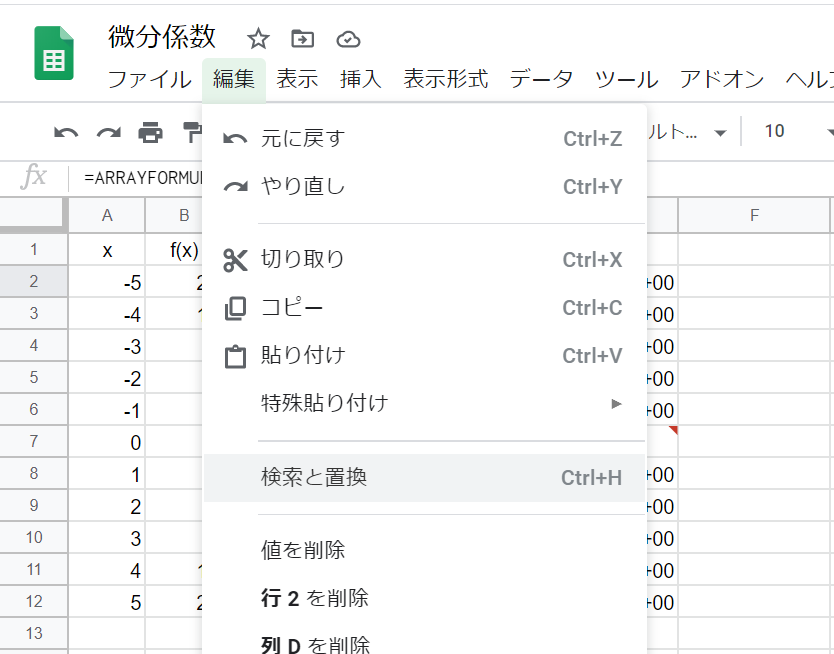
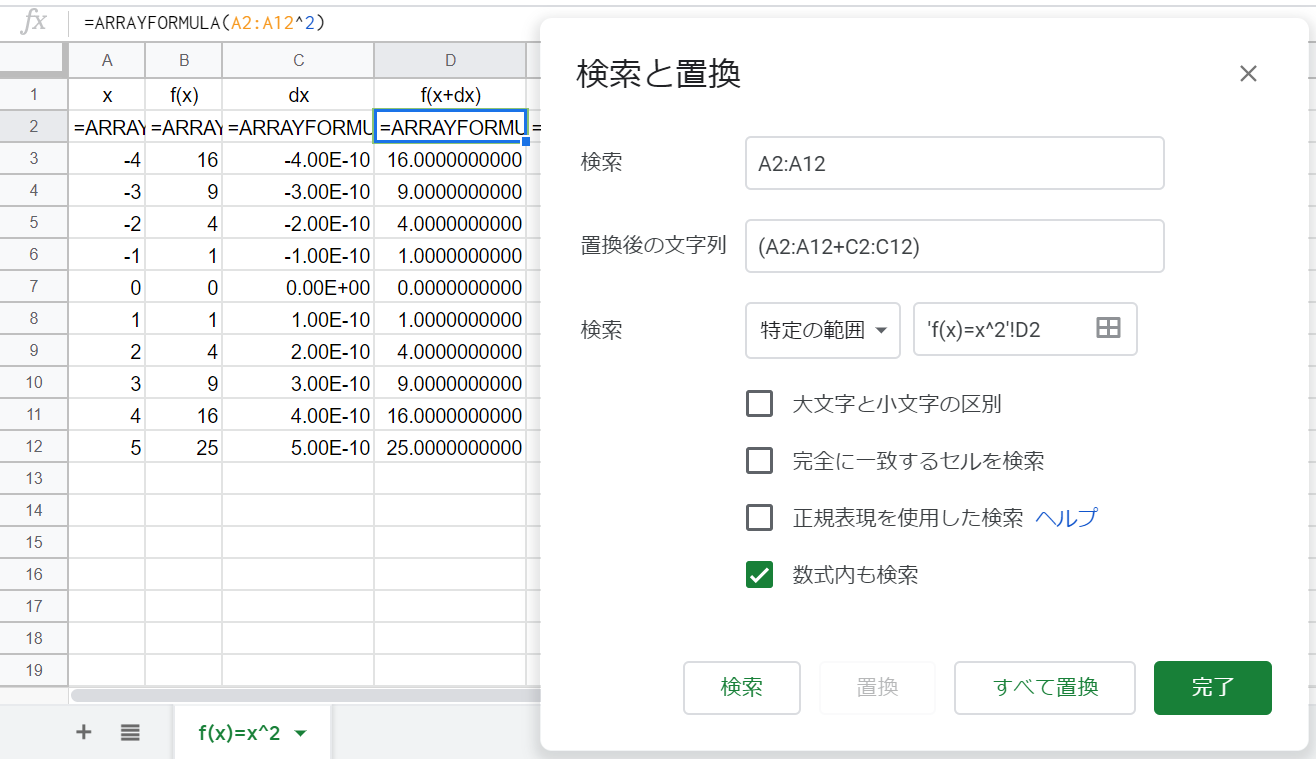
• 「編集」から「検索と置換」を選択。

• 下記のように入力。
  • 検索：A2:A12
  • 置換後の文字列：(A2:A12+C2:C12)
  • 検索：「特定の範囲」
  • 「数式内も検索」に☑

• 「すべて置換」し、「完了」

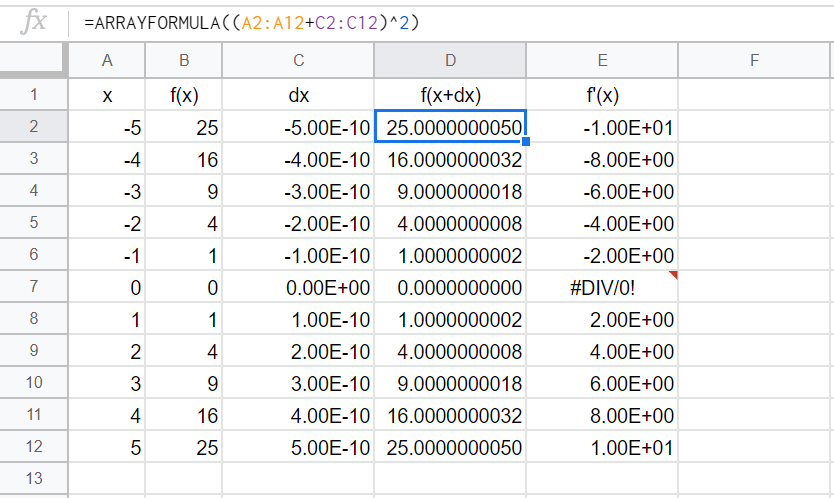
なんということだろう。D2セルの数式が完成しているではないか。

D2

=ARRAYFORMULA((A2:A12+C2:C12)^2)

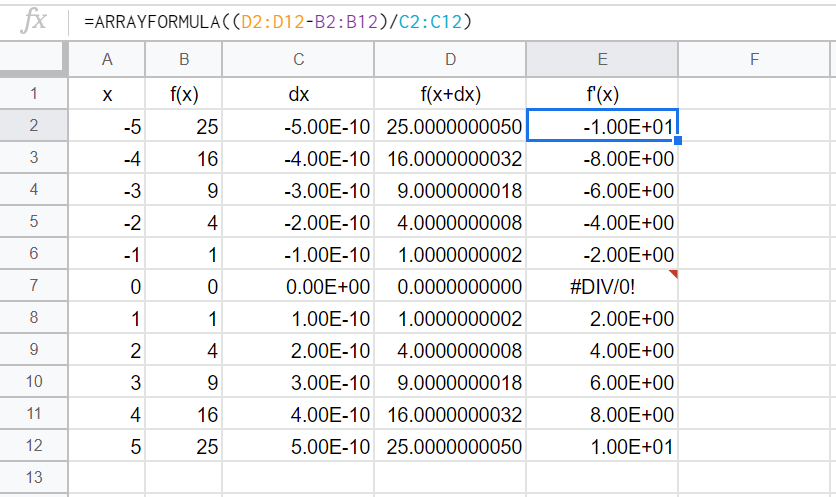
最後に、(f(x+dx)-f(x))/dxを計算する。

E2

=ARRAYFORMULA((D2:D12-B2:B12)/C2:C12)

これで、微分係数の当たりが付いた。

以上が、微分擬きの全容である。

おわりに

賢明な読者ならお気づきだと思うが、x=0で所謂"zero division error"が吐かれている。割と致命的な課題である。IF()の類いを使用して、回避する方法もあると思うが、今回は力尽きた。

また、D2セルにおいて、SUBSTITUTE()を使わなかったのは、返り値がテキストになってしまうためである。本当は関数だけで済ませたかった。

今後は、上記手法の応用例などの記事も書きたい。

それでは、また。