和牛子牛セリ価格の予測モデルの構築

目次

1. 自己紹介
2. はじめに
3. 概要
4. 環境
5. 成果物
6. 考察
7. 反省と課題
8. 感想

1. 自己紹介

現在、主に牛を対象とする家畜診療獣医師をしています。
今回、プログラミングスクールに通いPythonについて学ぶことができたので成果物を一つここに残したいと思います。
初めて成果物を一から作成したので、改善点等あれば遠慮なくコメントいただけると幸いです！

2. はじめに

皆さんは普段口にする牛肉がどのような血統なのか、どれほど大きく育った牛なのか、ということを考えたことはありますか？

おそらく多くの方がそのようなことを考えたことはないと思います。
しかし、繁殖和牛農家さんにとってはいかに良い牛を育てるのかが重要になってきます。
なにせそれがセリ価格に反映され、生活に直結しますからね。

今回は、普段の診療業務ではなくセリ市場の情報を分析して農家さんにそれを還元することで、農場経営の発展につなげてもらいたいと考え、セリ価格の予測モデル作成に取り組むこととしました。

3. 概要

和牛農家は、繁殖農家と肥育農家に大別されます。
あまり知られていませんが、一般に和牛は繁殖農家で産み育てられ10ヶ月齢前後で市場においてセリにかけられます。（ちなみに、雄は5ヶ月齢前後で去勢されます。）
それを肥育農家が買い取り、28ヶ月齢前後まで肥育された後に屠殺されお肉として皆さんの食卓へと並ぶのです。
今回は、繁殖農家で育てられた10ヶ月齢前後の和牛子牛のセリ情報1年分を活用して、血統や体重などに基づいたセリ価格の予測モデルを構築してみました。

4. 環境

OS：M1 Mac
言語：Python（Google Colaboratory）

5. 成果物

以下の流れで作成していきます。

5-1. 生データの確認
5-2. 必要なライブラリの読込み
5-3. データの取得
5-4. データの整形
5-5. ハイパーパラメータの最適化
5-6. モデルの学習・予測および予測精度の計算
5-7. 特徴量重要度の表示
5-8. 特徴量を選択してモデルの再学習・予測および予測精度の計算
5-9. 選択特徴量重要度の表示

5-1. 生データの確認

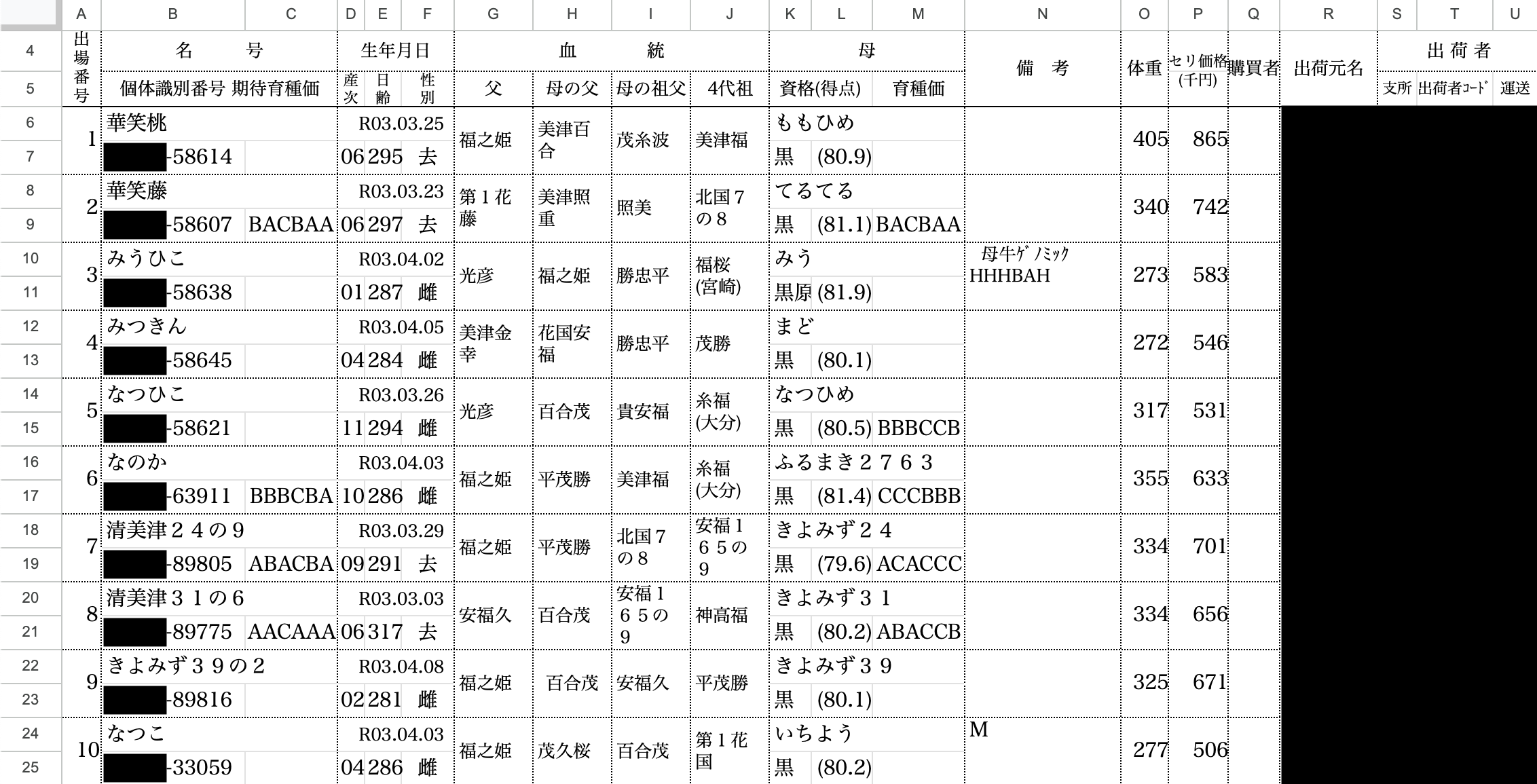
コーディングの前に今回使用するデータの中身をエクセルの状態で確認してみます。
ここでは、個体識別番号(一部)、集荷元名、出荷者名は個人情報にあたるため黒塗りで表示します。
ちなみに、個体識別番号というのは牛の耳標に書かれている10桁の数字であり、言わば牛のマイナ番号のような役割を果たしています。

5-2. 必要なライブラリの読込み

今回使用するGoogle Colaboratoryにおいて、japanize-matplotlibおよびoptunaは事前にインストールしておく必要があります。

!pip install japanize-matplotlib
!pip install optuna

import glob
import japanize_matplotlib
import lightgbm as lgb
import matplotlib.pyplot as plt
import numpy as np
import optuna
import pandas as pd
import seaborn as sns
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from google.colab import drive
drive.mount('/content/drive')

5-3. データの取得

それでは、エクセルファイルからデータを取得し中身を確認します。
なお、目的変数をセリ価格(千円)とし、説明変数には産次、日齢、性別、父、母の父、体重(kg)を用います。（後に体重/日齢を説明変数に加え、父および母の父はダミー変数化します。）

# フォルダからエクセルデータを取得
files = glob.glob('/content/drive/MyDrive/成果物/2022年子牛セリ価格/*.xlsx')
list_all = []
for file in files:
    list_all.append(pd.read_excel(file,
                                  skiprows=4,
                                  sheet_name='子牛',
                                  usecols=[1,3, 4, 5, 6, 7, 14, 15]).replace('_x000D_\n', ' ', regex=True).reset_index(drop=True))
df = pd.concat(list_all)
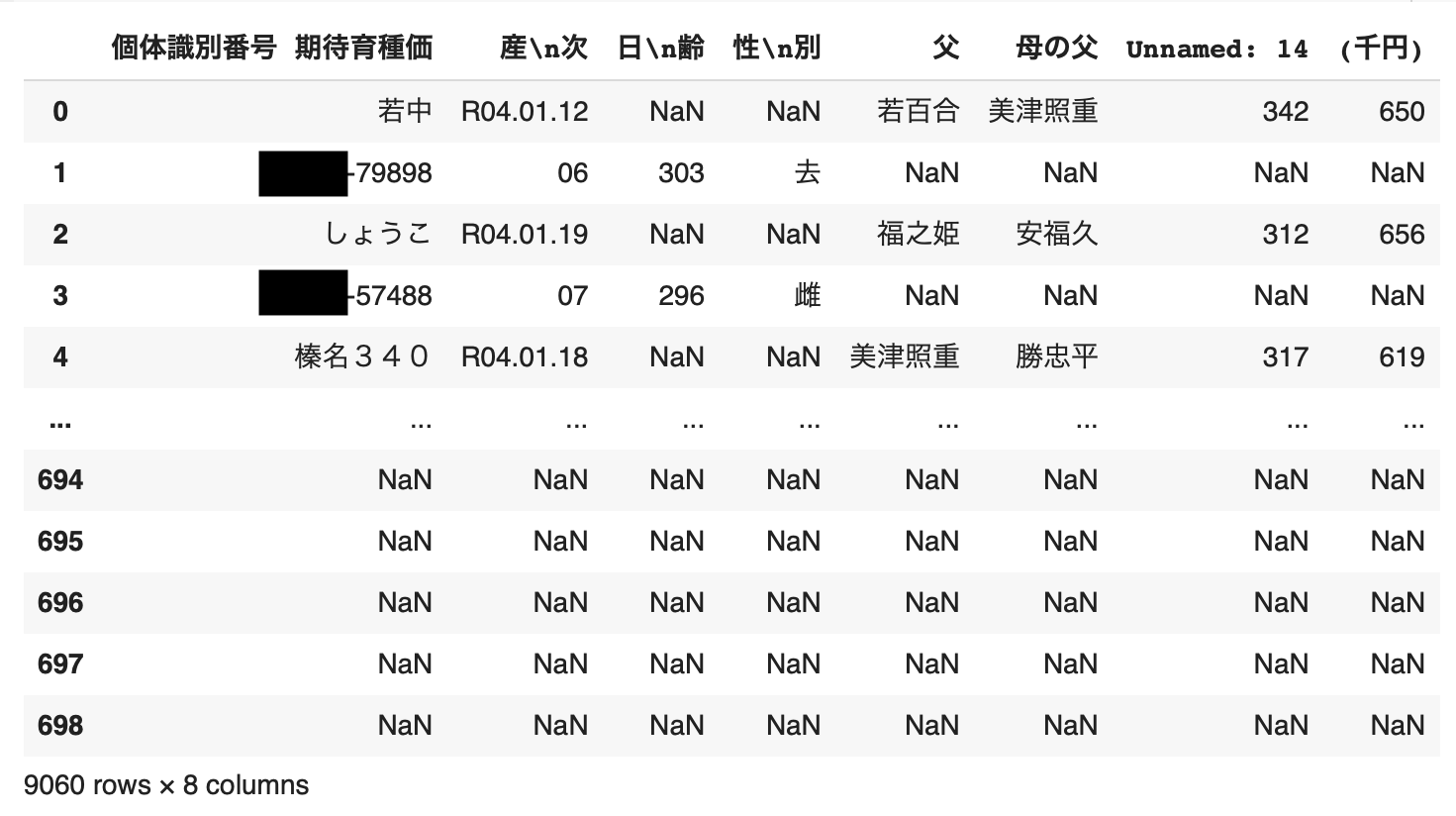
df

5-4. データの整形

各個体情報は2行にわたっており、奇数行には名号・父・母の父・体重(kg)・セリ価格(千円)、偶数行には個体識別番号・産次・日齢・性別のデータが入っているので、それぞれを変数名df_1,df_2に格納し、最終的に両者を結合します。
なお、再出荷により同一個体牛が存在する場合があるため、重複している名号および個体識別番号は区別して出力します。
では、まずはdf_1から整形します。

# 同一個体牛の区別
df.rename(columns={'個体識別番号 期待育種価':'名号/個体識別番号', '産\n次':'生年月日/産次', '日\n齢':'日齢', '性\n別':'性別', 'Unnamed: 14':'体重(kg)', '(千円)':'セリ価格(千円)'}, inplace=True)
df['区別'] = df.groupby('名号/個体識別番号').cumcount() + 1
df['名号/個体識別番号_区別'] = df['名号/個体識別番号'] + '_' + df['区別'].astype(str)
df = df[['名号/個体識別番号', '区別', '名号/個体識別番号_区別', '生年月日/産次', '日齢', '性別', '父', '母の父', '体重(kg)', 'セリ価格(千円)']].dropna(how="all")
df.to_excel('total.xlsx', index=False)

# 名号_区別、父、母の父、体重(kg)、セリ価格(千円)のデータを取得
df_1 = df.iloc[:, [2,6,7,8,9]].replace(['個体識別番号 期待育種価', '体重(kg)', 'セリ価格', '(千円)'], None, regex=True).dropna(thresh=3)
df_1.rename(columns={'名号/個体識別番号_区別':'名号_区別'}, inplace=True)
df_1

次に、df_2を整形します。

# 個体識別番号_区別、産次、日齢、性別のデータを取得
df_2 = df.iloc[:, 2:6].replace(['個体識別番号 期待育種価'], None, regex=True).dropna()
df_2.rename(columns={'名号/個体識別番号_区別':'個体識別番号_区別', '生年月日/産次':'産次'}, inplace=True)
df_2['産次'] = df_2['産次'].replace(['ET'], 99, regex=True)
df_2 = df_2.astype({'産次':'int16', '日齢':'int16'})
df_2

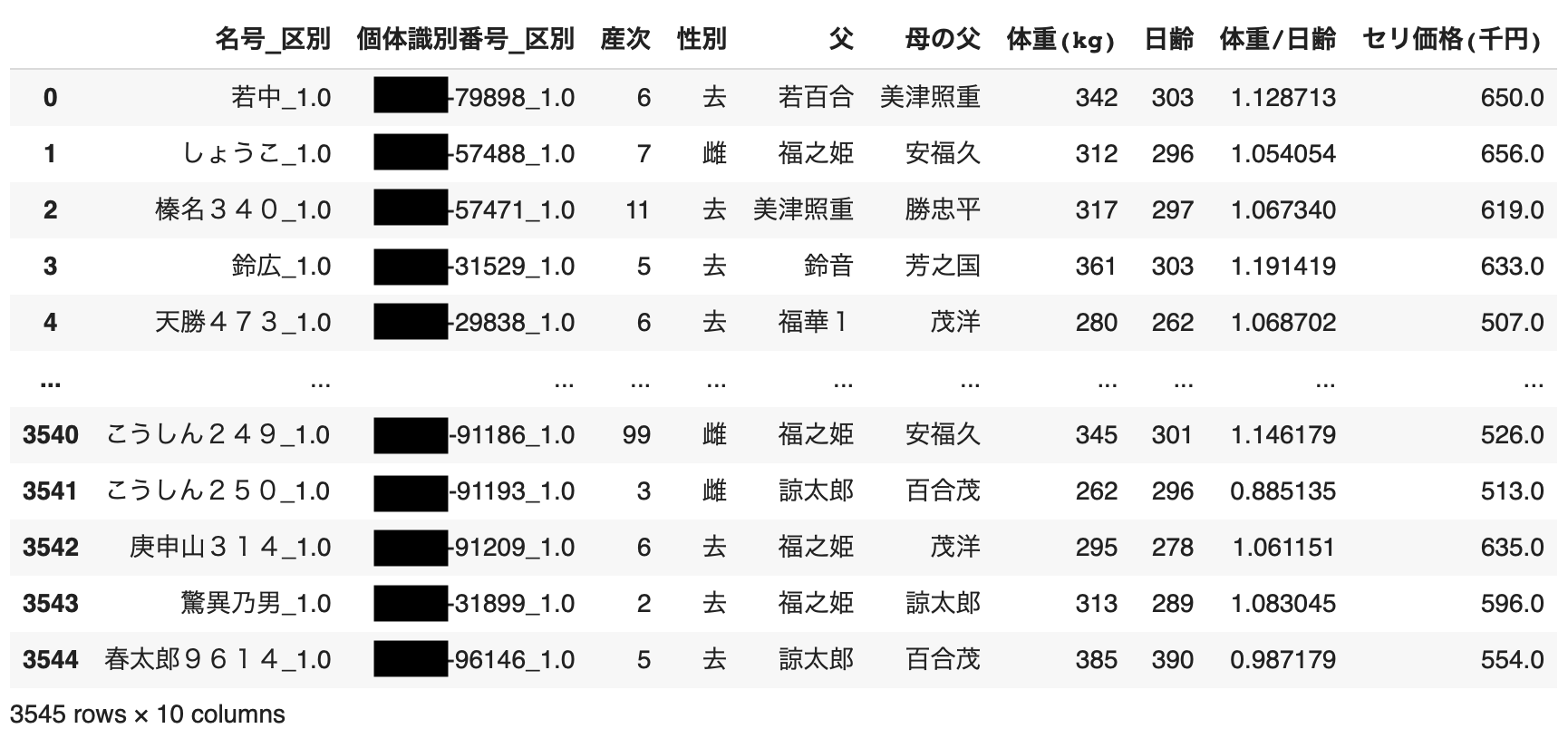
最後に、df_1とdf_2を結合します。
またここで、体重を日齢で割った値の列（体重/日齢）も追加します。
さらに、創傷などによりセリ価格が極端に低かったり、滅多に手に入らない種（精液）によって生まれた個体が極端に高かったりする場合が存在するので、これら外れ値については除外します。

# 名号および個体識別番号のデータをそれぞれ取得し、紐づける
name = df.iloc[:, 2].replace(['個体識別番号 期待育種価', '名\u3000\u3000\u3000号'], None, regex=True).dropna()[::2]
number = df.iloc[:, 2][1:].replace(['個体識別番号 期待育種価', '名\u3000\u3000\u3000号'], None, regex=True).dropna()[::2]
name_number_dic = dict(zip(name, number))

# df_1とdf_2を結合する
df_1['個体識別番号_区別'] = df_1['名号_区別'].map(name_number_dic)  # df_1とname_number_dicを紐づける
edit_df = pd.merge(df_1, df_2, on='個体識別番号_区別', how='inner')
edit_df = edit_df[edit_df['性別']!='雄'].dropna().reset_index(drop=True)  # 性別が雄の行および体重・セリ価格がNanの行を削除
edit_df = edit_df.astype({'体重(kg)':'int16', '日齢':'int16', 'セリ価格(千円)':'float64'})  # 体重を日齢で割った値の列を追加
edit_df['体重/日齢'] = edit_df['体重(kg)'] / edit_df['日齢']
edit_df = edit_df.reindex(columns=['名号_区別', '個体識別番号_区別', '産次', '性別', '父', '母の父', '体重(kg)', '日齢', '体重/日齢', 'セリ価格(千円)'])

# セリ価格(千円)の箱ひげ図を作成しデータ点をプロットする
edit_df['セリ価格(千円)'] = pd.to_numeric(edit_df['セリ価格(千円)'], errors='coerce')
Q1 = edit_df['セリ価格(千円)'].quantile(0.25)
Q3 = edit_df['セリ価格(千円)'].quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

plt.figure(figsize=(10, 6))
sns.boxplot(x=edit_df['セリ価格(千円)'], boxprops=dict(facecolor='blue', edgecolor='black', linewidth=2.0))
sns.swarmplot(x=edit_df['セリ価格(千円)'], color='red', size=3)
plt.title('セリ価格の箱ひげ図')
plt.grid()
plt.show()

# 外れ値を除外
edit_df = edit_df[(edit_df['セリ価格(千円)'] >= lower_bound) & (edit_df['セリ価格(千円)'] <= upper_bound)].reset_index(drop=True)
edit_df

5-5. ハイパーパラメータの最適化

これでデータの整形が完了しました。
次にモデルの学習および予測を行っていくのですが、その前にモデルのハイパーパラメータを最適化します。
なお、学習フレームワークにはLightGBMを、ハイパーパラメータの最適化にはOptunaを用います。

# 特徴量を説明変数と目的変数に分割(説明変数の一部はダミー変数処理を行う)
df_X = edit_df.drop(['名号_区別', '個体識別番号_区別', 'セリ価格(千円)'], axis=1)
df_X = pd.get_dummies(df_X, columns=['性別', '父', '母の父'])
df_y = edit_df['セリ価格(千円)'].astype('float64')

test_size=0.3
random_state = 42
seed = 42

# 説明変数と目的変数をそれぞれ学習データとテストデータに分割(7:3)
X_trainval, X_test, y_trainval, y_test = train_test_split(df_X, df_y, test_size=test_size, shuffle=False, random_state=random_state)
# 説明変数と目的変数の学習データをそれぞれ訓練用と検証用に分割(7:3)
X_train, X_valid, y_train, y_valid = train_test_split(X_trainval, y_trainval, test_size=test_size, shuffle=False, random_state=random_state)

# Optunaの準備
def objective(trial):

    # LightGBM用にデータセットを作成
    lgb_train = lgb.Dataset(X_train, y_train, feature_name=[str(i) for i in range(X_train.shape[1])])
    lgb_val = lgb.Dataset(X_valid, y_valid, reference=lgb_train, feature_name=[str(i) for i in range(X_valid.shape[1])])
    
    # ハイパーパラメータの探索範囲を設定
    param = {
            'task': 'train',
            'boosting_type': 'gbdt',
            'objective': 'regression',
            'metric': 'rmse',
            'verbosity': -1,
            'lambda_l1': trial.suggest_float('lambda_l1', 1e-8, 10.0, log=True),
            'lambda_l2': trial.suggest_float('lambda_l2', 1e-8, 10.0, log=True),
            'num_leaves': trial.suggest_int('num_leaves', 2, 256),
            'feature_fraction': trial.suggest_float('feature_fraction', 0.4, 1.0),
            'bagging_fraction': trial.suggest_float('bagging_fraction', 0.4, 1.0),
            'bagging_freq': trial.suggest_int('bagging_freq', 1, 7),
            'min_child_samples': trial.suggest_int('min_child_samples', 5, 100),
            'learning_rate': trial.suggest_float('learning_rate', 1e-4, 1.0, log=True),
            'random_state': random_state,
            'bagging_seed': seed,
            'feature_fraction_seed':seed,
            'deterministic': True,  # 計算の再現性を保証
            'force_row_wise': True  # 計算の再現性を向上
            }

    # モデルの作成
    model = lgb.train(
                     params=param,
                     train_set=lgb_train,
                     valid_sets=[lgb_train, lgb_val],
                     valid_names=['Train', 'Valid'],
                     num_boost_round=500,
                     callbacks=[lgb.early_stopping(stopping_rounds=50, verbose=1),
                                lgb.log_evaluation(100)]
                     )
                     
    # 調整後モデルで予測の実行
    y_valid_pred = model.predict(X_valid, num_iteration=model.best_iteration)
    rmse = mean_squared_error(y_valid, y_valid_pred, squared=False)

    return rmse

# Optunaの実行
study = optuna.create_study(direction='minimize', sampler=optuna.samplers.TPESampler(seed=42))
study.optimize(objective, n_trials=100)

# 最適なハイパーパラメータの表示
print('Number of finished trials:', len(study.trials))
print('Best trial:')
trial = study.best_trial
print('Value: {:.5f}'.format(trial.value))
print('Params: ')
for key, value in trial.params.items():
    print('    {}: {}'.format(key, value))

5-6. モデルの学習・予測および予測精度の計算

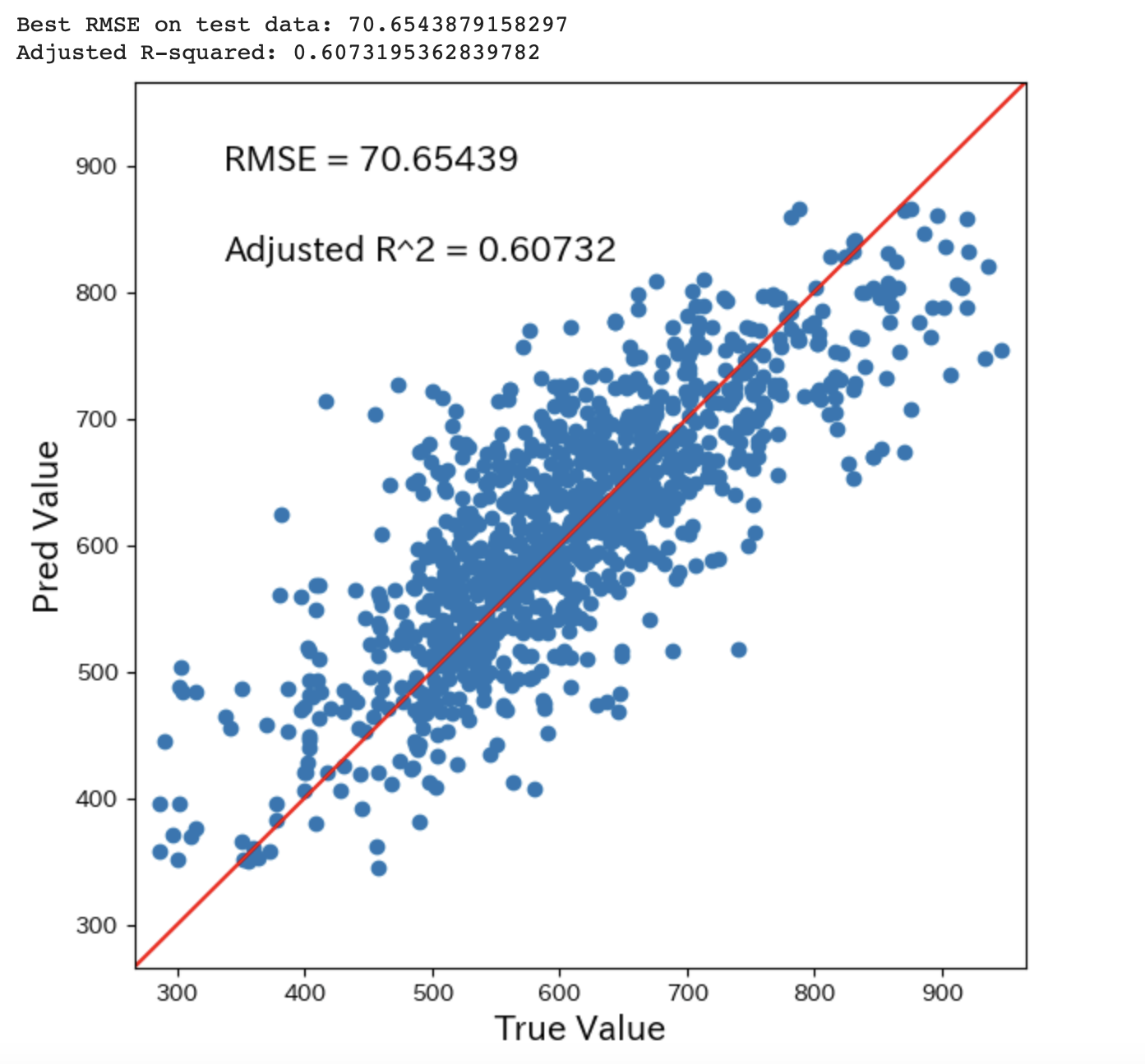
最適なハイパーパラメータを求めることができたので、これを用いてモデルの学習を行い、そのモデルを用いて目的変数の予測を行います。
さらに予測値と真値の関係をプロットし、RMSEおよび自由度調整済み決定係数によりモデルの性能を評価します。

# 最適なハイパーパラメータで学習
lgb_train = lgb.Dataset(X_train, y_train, feature_name=[str(i) for i in range(X_train.shape[1])], free_raw_data=False)
lgb_val = lgb.Dataset(X_valid, y_valid, reference=lgb_train, feature_name=[str(i) for i in range(X_valid.shape[1])], free_raw_data=False)

best_params = study.best_trial.params

best_model = lgb.train(
                      params=best_params,
                      train_set=lgb_train,
                      valid_sets=[lgb_train, lgb_val],
                      valid_names=['Train', 'Valid'],
                      num_boost_round=500,
                      callbacks=[lgb.early_stopping(stopping_rounds=50, verbose=1),
                                 lgb.log_evaluation(100)]
                      )

# テストデータで予測
y_test_pred = best_model.predict(X_test, num_iteration=best_model.best_iteration)

# 予測精度を計算
rmse_best = mean_squared_error(y_test, y_test_pred, squared=False)

# 予測値と真値の可視化およびモデルの評価
def True_Pred_map(pred_df):
    RMSE = np.sqrt(mean_squared_error(pred_df['true'], pred_df['pred']))
    R2 = r2_score(pred_df['true'], pred_df['pred'])

    n = len(pred_df)
    k = X_train.shape[1]
    adjusted_R2 = 1 - (1 - R2) * (n - 1) / (n - k - 1)  # 自由度調整済み決定係数を計算

    print(f'Best RMSE on test data: {rmse_best}')
    print(f'Adjusted R-squared: {adjusted_R2}')

    plt.figure(figsize=(8,8))
    ax = plt.subplot(111)
    ax.scatter('true', 'pred', data=pred_df)
    ax.set_xlabel('True Value', fontsize=15)
    ax.set_ylabel('Pred Value', fontsize=15)
    ax.set_xlim(pred_df.min().min()-20 , pred_df.max().max()+20)
    ax.set_ylim(pred_df.min().min()-20 , pred_df.max().max()+20)
    x = np.linspace(pred_df.min().min()-20, pred_df.max().max()+20, 2)
    y = x
    ax.plot(x, y, 'r-')
    plt.text(0.1, 0.9, 'RMSE = {}'.format(str(round(RMSE, 5))), transform=ax.transAxes, fontsize=15)
    plt.text(0.1, 0.8, 'Adjusted R^2 = {}'.format(str(round(adjusted_R2, 5))), transform=ax.transAxes, fontsize=15)

pred_df = pd.concat([y_test.reset_index(drop=True), pd.Series(y_test_pred)], axis=1)  # 予測値と真値を可視化関数用に加工
pred_df.columns = ['true', 'pred']

True_Pred_map(pred_df)  # 可視化関数の起動

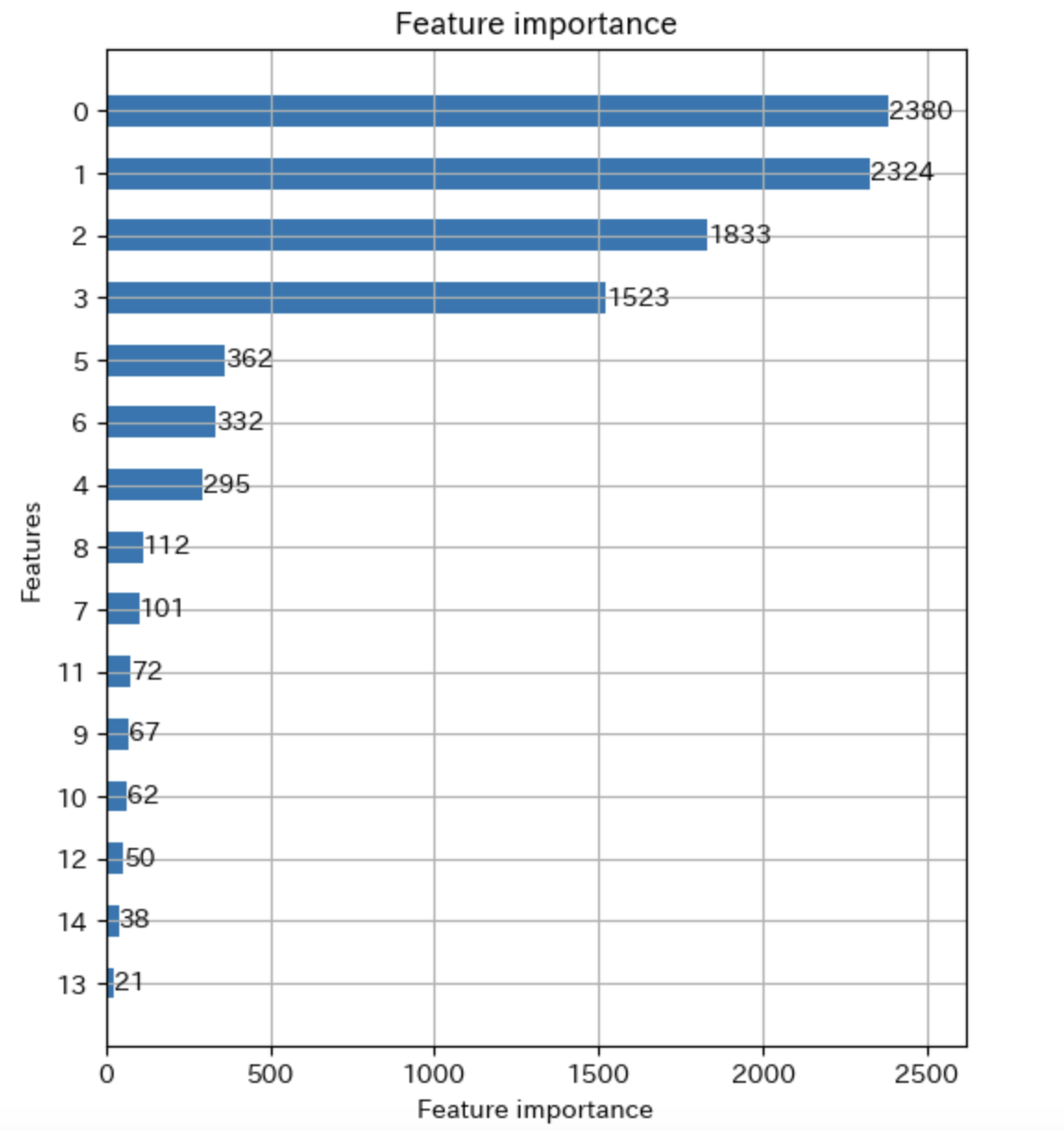
5-7. 特徴量重要度の表示

特徴量重要度を表示してみます。
ここでは特徴量重要度をグラフで表示すると特徴量名ではなくインデックス番号が表示されてしまうため、特徴量名がわかるデータフレームも併せて表示してみます。
なお、データフレームは特徴量重要度の上位15個を表示します。

# 特徴量重要度をグラフで表示
lgb.plot_importance(best_model, height=0.5, figsize=(6,10))

# 特徴量重要度上位15個をデータフレームで表示
importance = pd.DataFrame(best_model.feature_importance(), index=df_X.columns, columns=['importance'])
importance = importance.sort_values('importance', ascending=False)
display(importance.head(15))

5-8. 特徴量を選択してモデルの再学習・予測および予測精度の計算

モデル性能の向上を目的に、特徴量を特徴量重要度上位15個に絞ってモデルの再学習を行います。

# 特徴量重要度の上位15個の特徴名を取得
top15_features = importance.head(15).index.tolist()

# 新しい説明変数セットを作成（上位15個の特徴のみを含む）
X_train_top15 = X_train[top15_features]
X_valid_top15 = X_valid[top15_features]
X_test_top15 = X_test[top15_features]

# 新しいデータセットの準備
lgb_train_top15 = lgb.Dataset(X_train_top15, y_train, feature_name=[str(i) for i in range(X_train_top15.shape[1])], free_raw_data=False)
lgb_val_top15 = lgb.Dataset(X_valid_top15, y_valid, reference=lgb_train_top15, feature_name=[str(i) for i in range(X_valid_top15.shape[1])], free_raw_data=False)

# 最適なハイパーパラメータで学習
best_model_top15 = lgb.train(
    params=best_params,
    train_set=lgb_train_top15,
    valid_sets=[lgb_train_top15, lgb_val_top15],
    valid_names=['Train', 'Valid'],
    num_boost_round=500,
    callbacks=[lgb.early_stopping(stopping_rounds=50, verbose=1),
               lgb.log_evaluation(100)]
)

# テストデータで評価
y_test_pred_top15 = best_model_top15.predict(X_test_top15, num_iteration=best_model_top15.best_iteration)

# 予測精度を計算
rmse_best_top15 = mean_squared_error(y_test, y_test_pred_top15, squared=False)

# 予測値と真値の可視化およびモデルの評価
def True_Pred_map(pred_df_top15):
    RMSE = np.sqrt(mean_squared_error(pred_df_top15['true'], pred_df_top15['pred']))
    R2 = r2_score(pred_df_top15['true'], pred_df_top15['pred'])

    n = len(pred_df_top15)
    k = X_train_top15.shape[1]
    adjusted_R2 = 1 - ((1 - R2) * (n - 1) / (n - k - 1))  # 自由度調整済み決定係数を計算

    print(f'Best RMSE on test data: {rmse_best_top15}')
    print(f'Adjusted R-squared: {adjusted_R2}')

    plt.figure(figsize=(7,7))
    ax = plt.subplot(111)
    ax.scatter('true', 'pred', data=pred_df_top15)
    ax.set_xlabel('True Value', fontsize=15)
    ax.set_ylabel('Pred Value', fontsize=15)
    ax.set_xlim(pred_df_top15.min().min()-20 , pred_df_top15.max().max()+20)
    ax.set_ylim(pred_df_top15.min().min()-20 , pred_df_top15.max().max()+20)
    x = np.linspace(pred_df_top15.min().min()-20, pred_df_top15.max().max()+20, 2)
    y = x
    ax.plot(x, y, 'r-')
    plt.text(0.1, 0.9, 'RMSE = {}'.format(str(round(RMSE, 5))), transform=ax.transAxes, fontsize=15)
    plt.text(0.1, 0.8, 'Adjusted R^2 = {}'.format(str(round(adjusted_R2, 5))), transform=ax.transAxes, fontsize=15)

pred_df_top15 = pd.concat([y_test.reset_index(drop=True), pd.Series(y_test_pred_top15)], axis=1)  # 予測値と真値を可視化関数用に加工
pred_df_top15.columns = ['true', 'pred']

True_Pred_map(pred_df_top15)  # 可視化関数の起動

5-9. 選択特徴量重要度の表示

最後に、選択した15個の特徴量を用いて再学習・予測したモデルの特徴量重要度を示します。

# 特徴量重要度をグラフで表示
lgb.plot_importance(best_model_top15, height=0.5, figsize=(6,10))

# 特徴量重要度をデータフレームで表示
importance_top15 = pd.DataFrame(best_model_top15.feature_importance(), index=top15_features, columns=['importance'])
importance_top15 = importance_top15.sort_values(by='importance', ascending=False)
display(importance_top15)

6. 考察

今回はLightGBMを用いて予測モデルを2度作成しましたが、再作成したモデルにおいてRMSE(二乗平均平方根誤差)および自由度調整済み決定係数の改善がみられました。
RMSEの改善は、特徴量重要度に基づいて特徴量を選択することで過学習が緩和され、モデルが未知データに対しても良い予測を行うようになったためと考えられます。
また、自由度調整済み決定係数の改善も同様に、特徴量重要度に基づいて特徴量を選択したことが要因と思われます。つまり、ノイズを削除して影響力のある特徴量のみを使用することで、モデルの汎化能力が向上したため新しいデータに対する予測精度が高まったのだと考えられます。

7. 反省と課題

実は血統については、各種が『田尻系』・『気高系』・『藤良系』などの様々な系統に大別されます。
同じ系統が世代間で続いてしまうといわゆる近親交配になってしまい、出生子牛の奇形や病原抵抗力の低下、成長速度の低下などのリスクがあるので、畜主や授精師は、系統が母の父・母の祖父・4代祖となるべく重複しないよう父の種を選んで人工授精を行なっています。
しかし、今回の予測モデルでは系統の関連までを考慮しておらず、単純に父と母の父をダミー変数化して説明変数に用いました。
今後はその点を改善したモデルを作る必要があると思います。
ただ、系統までを考慮したモデルを作るとなると、説明変数の数が増えることによりモデルが過学習を起こしてしまったり、モデルの解釈性が低下してしまったりなどの弊害が起きてしまいます。
これらを解決するには今回のような特徴量選択や正則化、あるいは次元削減などの対策が考えられるので、それらをうまく活用してモデル作成に挑みたいと思います。

8. 感想

体重が大きかったり、人気のある血統である方がやはりセリ価格は高くなるイメージが感覚的に強かったのですが、父または母の父にどの血統が入っているとセリ価格に寄与するのかということが客観的に数値で確認することができたので、これまでの感覚で理解していたことが腑に落ちました。
また、単純な体重の大きさよりも日齢に対して体重がどれほどなのかということの方がより重要性が高い可能性があると分かり、新たな発見をすることができました。
初めて成果物を作ってみましたが、正直コードを書き上げるのも大変で、期待する結果を得るのもなかなか難しいなと感じました。ただ、毎日のようにPythonに触れていても全く飽きません。まだまだ学ぶことは沢山あるので、これからも精進していきたいと思います。
ここまで読んでいただきありがとうございました。