その4
今回こそ、CPU本体の製作に入ろう。本「CPUの創りかた」では、ROMの次にレジスタを作る流れになっている。
ただ、いきなりレジスタはしんどいので、今回はその手前のFlip Flopの話だ。
Flip Flopと状態保持
Flip Flopは順序回路の一つらしいが、状態を記憶することができるらしい(習った気はするがとっくに忘れた)。だから「レジスタ」は値を保持できるというわけだ。
ではHaskellで「状態を記憶する」にはどうしたらいいのか? オブジェクト指向言語であれば、オブジェクト内に状態を持つなんてのは普通にできるので簡単だが、Haskellである。「状態」って無いのでは?無理?
調べると、HaskellにはStateモナドなるものがあり、これを使うと何かできそうな匂いはする。が、解説を読んでもちっともわからないのであきらめた。仕方がないので全ての「状態」は外で管理することにしてしまおう。ROMの時と同じく、毎回「状態」も入力し、出力には「状態」を含める。その「状態」を次の入力にする。面倒だがそうすることで「状態」は管理できるだろう。
という方針(?)に基づき、Flip Flopを作っていく。
S-R Flip Flop
まずは基本中の基本(?)のS-R Flip Flop(以下、SR-FFとする)から。Flip Flopについては「CPUの創りかた」にも多少説明はあるのだがいまいちピンとこない。もう少し詳しいことが知りたかったのでこの本も買った。
「ゼロから学ぶディジタル論理回路」(秋田 純一 著、講談社)
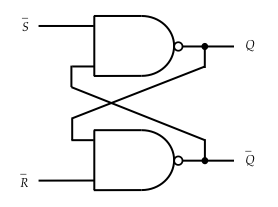
これによると、SR-FFの回路図は次のとおりである。
回路自体は単純だが、出力($Q$、$\overline{Q}$)がフィードバックしているところをどう処置するかである。ただ、上述の通り今回は「状態」を関数などの内部に持たず毎回入力するので、それほど悩まなくてもいいかもしれない。なお、コード中では$\overline{Q}$のように上線が書けないため、'で代用している。
{- |
SR-FlipFlop
IN : [S,R,Q,!Q]
OUT: [Q,!Q]
-}
lc_srff :: LogicCircuit
lc_srff (s:r:q0:q0':_) = [q, q']
where
q_ = head $ lc_nand [s, q0']
q' = head $ lc_nand [r, q_]
q = head $ lc_nand [s, q']
一旦、$Q$について仮の出力を得て、それを$\overline{Q}$の方に回してそれを得る。さらにそれを入力として、あらためて$Q$を得るわけだ。なおソース中のq'は$\overline{Q}$である。ちなみにこのSR-FFは負論理だ(セット/リセットの時は$S$、$R$をLOにする)。
SR-FFの真理値表は次のようである。
| $S$ | $R$ | $Q$ | $\overline{Q}$ | remarks |
|---|---|---|---|---|
| L | L | - | - | 禁止 |
| L | H | H | L | セット |
| H | L | L | H | リセット |
| H | H | ? | ? | 変化しない |
幾つかのWebサイトで真理値表を確認したが、$S$と$R$を両方LOにするのは「禁止」らしい。実際にそうしたらどうなるか回路図で追いかけてみたら、$Q$も$\overline{Q}$もHIになり$Q=\overline{Q}$となってわけがわからなくなるようだ。だが上記コードでは$S$、$R$ともにLOが入力されたらエラーとはせず、回路図の通り$Q$も$\overline{Q}$もHIを出力することにした。入力・出力をどう扱うかは使う人が対応することだ(自分だが…・)。
以下はdoctestのコードだ。
>>> lc_srff [sLO, sLO, sLO, sLO] == [sHI,sHI]
True
>>> lc_srff [sLO, sHI, sHI, sLO] == [sHI,sLO]
True
>>> lc_srff [sHI, sLO, sHI, sLO] == [sLO,sHI]
True
>>> lc_srff [sHI, sHI, sHI, sLO] == [sHI,sLO]
True
>>> lc_srff [sHI, sHI, sLO, sHI] == [sLO,sHI]
True
-- あってはいけない(Q=!Q)状態を入力
>>> lc_srff [sHI, sHI, sLO, sLO] == [sHI,sLO]
True
>>> lc_srff [sHI, sHI, sHI, sHI] == [sLO,sHI]
True
最後に、ここで作ったSR-FFの真理値表を示す。テストコードの最後の二つも本来あってはいけないものだが、なんとなく値を返しているのはコードでの処理の仕方によるものなので物理的な回路とは異なるかもしれないがご愛嬌。
| $S$ | $R$ | old $Q$ | old $\overline{Q}$ | new $Q$ | new $\overline{Q}$ |
|---|---|---|---|---|---|
| L | L | ? | ? | H | H |
| L | H | ? | ? | H | L |
| H | L | ? | ? | L | H |
| H | H | L | H | L | H |
| H | H | H | L | H | L |
| H | H | L | L | H | L |
| H | H | H | H | L | H |
('?'はLO/HIどちらでもよいという意味)
エッジトリガ式 D Flip Flop
解説書などではS-Rの次は同期式S-RとかJK Flip Flopとか色々話が続くのだが、どうやらCPUで実際に使われるのは「エッジトリガ式 D Flip Flop」だそうだ。これは、clockの立ち上がり(or 立ち下がり)の瞬間の$D$の値を保持するらしい。エッジトリガ式D Flip-Flopは長いので以後D-FFとし、値はクロックの立ち上がり時に変化することとする。
ということで、D-FFはクロックの立ち上がり時の$D$の値を保持する=出力するのだから、真理値表は次のようになるだろう。
| $D$ | $Q$ | $\overline{Q}$ |
|---|---|---|
| L | L | H |
| H | H | L |
なんと単純な!これなら超簡単にコードにできる。
lc_dff :: LogicCircuit
lc_dff (d:_) = [d, not d]
テストはこう。
>>> lc_dff [sLO] == [sLO,sHI]
True
>>> lc_dff [sHI] == [sHI,sLO]
True
テストもちゃんと通る!難関と思っていたD-FFがいとも簡単に実装できてしまった!いやいやいやいや、そういうわけにはいかない。これだと以前のdecorderの時と同じだ。ここはやはり、ちゃんと論理回路をコードで表現して結果を得ないと。
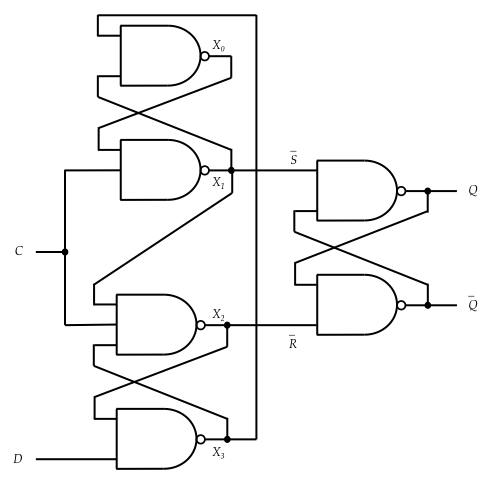
D-FFの回路として、先の本(ゼロから学ぶディジタル論理回路)に記載されている6NAND型 D Flip-Flopを採用しよう。回路図は以下の通り。
これをコードにしたいわけだがここで問題がある。クロックの立ち上がりなので$C$=HIであるから、$X_1$は$X_0$がわからないと決まらない。$X_0$は$X_1$と$X_3$が決まらないとわからない。ということで、結局入力$D$がHIかLOか分かっていても$X_n$を決められない。さてどうするか。
今回、論理回路を表す関数はその呼出しの瞬間がクロックの立ち上がりと決めた。であれば、その「直前」はクロック入力$C$=LOということだ。そう考えて上の回路図を見直すと、$C$=LOだから$X_1$と$X_2$はHIと決まる。$X_3$は$D$と$X_2$から決まる。$X_0$も$X_1$と$X_3$から決まるわけだ。これで直前の状態が決まった。
次に$C$=HIとして各値を求めよう。すでに$X_n$は求めているからそれを使えば新しい$X_1$と$X_2$が得られる。回路図の右半分はSR-FFそのままだからそいつに入力してやればよい。。。いや、本当にそうか?
$\overline{S}$と$\overline{R}$がともにHIだったら「現状維持」となり、そのためには「現状」がわからないとやっぱりダメだ。
うーん、とりあえずどういう状態になるか調べてみることにする。$D$と$X_n$の真理値表を書いてみた。クロックの立ち上がり前後があればわかりやすいので$C$もつけた。
| $D$ | $C$ | $X_0$ | $X_1$ | $X_2$ | $X_3$ |
|---|---|---|---|---|---|
| L | L | L | H | H | H |
| L | H | L | H | L | H |
| H | L | H | H | H | L |
| H | H | H | L | H | L |
$D$がLOのときにクロックが立ち上がる前と後の$X_n$を並べた。SR-FFの入力は、$S=X_1$、$R=X_2$であるから、クロックの立ち上がり($C$=HI)時のそれぞれの値を見てみると、$D$がHIでもLOでも$X_1=\overline{X_2}$である。であればSR-FFへの入力は常に値のセットもしくはリセットとなるため、過去の状態に関わらず必ず$Q$と$\overline{Q}$が決まることになる!悩む必要はないわけだ。
上記を踏まえてコードに落としてみたのが以下。
lc_dff :: LogicCircuit
lc_dff (d:_) = lc_srff (x1' ++ x2' ++ [sLO, sHI])
where
-- before rising (C = LO)
x1 = [sHI] -- because C = LO
x2 = [sHI] -- because C = LO
x3 = lc_nand (d ++ x2)
x0 = lc_nand (x1 ++ x3)
-- rising edge (C = HI)
x1' = lc_nand ([sHI] ++ x0)
x2' = lc_nand ([sHI] ++ x1' ++ x3)
先の論理回路を使わない方をlc_dff'と改名して比較テスト。
>>> lc_dff [sLO] == lc_dff' [sLO]
True
>>> lc_dff [sHI] == lc_dff' [sHI]
True
ちゃんとテストも通る!
ClearとPresetの追加
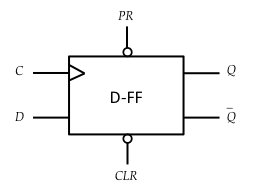
さて、D-FFを実際に使うとしたらClear($CLR$)やPreset($PR$)ができないとだめだろう。特にClearはシステムの起動時のリセット処理で必要となる。ということで、次のようなモジュールにしよう。ClearとPresetはともに負論理とする。
このようなモジュールが入ったICもあるようだが、その論理回路はややこしいみたいなので勝手に仕様を決めてしまうことにする。
- Clearしたいときは$CLR$=LOにする。その時はPresetや$D$の値によらず$Q$はLOにする。
- Presetしたいときは$CLR$=HIかつ$PR$=LOにする。その時は$D$の値によらず$Q$はHIにする。
- $CLR$=$PR$=HIなら、$D$の値を$Q$に出力する。
これを満足するように$CLR$、$PR$、$D$の3つの値から、新たに$D'$を作ろう。D-FFなので結果的に$D'=Q$である。上の仕様を真理値表にすると以下のようになる。'?'はHI/LO両方を表す。
| $CLR$ | $PR$ | $D$ | $D’$(=$Q$) |
|---|---|---|---|
| L | ? | ? | L |
| H | L | ? | H |
| H | H | L | L |
| H | H | H | H |
これを論理回路にしよう。$CLR$、$PR$、$D$の3入力から$D’$を得る式を検討する。結論を書くと次のようになる。ちなみに(超単純ではあるが)カルノー図を描いたのは20年ぶりぐらいかな?
$
D' = CLR \cdot (\overline{PR} + D)
$
これを踏まえ、$CLR$、$PR$付きのD-FFを次のように定義しよう。
lc_dff_cp :: LogicCircuit
lc_dff_cp (c:p:d:_) = lc_dff d'
where
d' = lc_and ([c] ++ lc_or (lc_not [p] ++ [d]))
まあ、そのまんまなんだが。ついでにテストは以下。うまく動いているようだ。
>>> lc_dff_cp [sLO, sLO, sLO] == [sLO,sHI]
True
>>> lc_dff_cp [sLO, sLO, sHI] == [sLO,sHI]
True
>>> lc_dff_cp [sLO, sHI, sLO] == [sLO,sHI]
True
>>> lc_dff_cp [sLO, sHI, sHI] == [sLO,sHI]
True
>>> lc_dff_cp [sHI, sLO, sLO] == [sHI,sLO]
True
>>> lc_dff_cp [sHI, sLO, sHI] == [sHI,sLO]
True
>>> lc_dff_cp [sHI, sHI, sLO] == [sLO,sHI]
True
>>> lc_dff_cp [sHI, sHI, sHI] == [sHI,sLO]
True
これで、やっとレジスタに使えるD-FFが得られた。
まとめ
今回はFlip Flop、特にCPUで使うエッジトリガ式D Flip Flopを作った。次回はこれを多数並べて、いよいよレジスタを作ることにしよう。
(ここまでのソースはこちら)
※ 現在のソースは執筆時点から色々変更されている。