[checkio] Counting Tiles

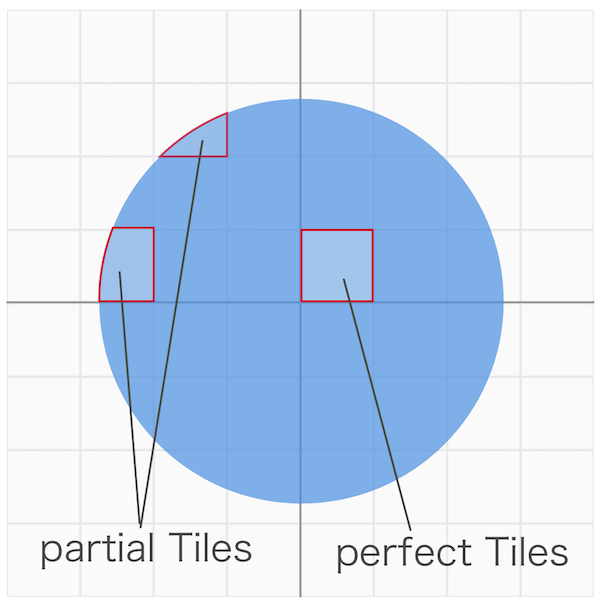
今回のお題は正方形タイルが8x8で敷き詰められた戦場に、円の半径ニキが出陣し、その半径ニキの爆心エリアに巻き込まれるかわいそうなタイルたちを、完全消失のものと部分消失のものを分けてそれぞれ数えよというもの。

イメージ：

どうしろっていうんだ！と最初は解き方がわからず、数学嫌いだった高校生活を呪った。
だがしかし、以下の啓示が天より舞い降り、
・円を４分割して考える。
・左上の円に限って見てみる。
・半径と、そのタイルの左上と右下の中心からの距離を比べ、前者が真の場合は完全なタイル、後者が真の場合は部分的に含まれるタイルとなる。
これで解けるやんけということで無事生還。

自分の回答

function countingTiles(radius){
    
    //variables
    let peT = 0;
    let paT = 0;
    let bigRad = Math.ceil(radius);
    
    countTiles(bigRad, radius);
    peT*=4;
    paT*=4;
    
    //counting up mates
    function countTiles(a, b) {
        for (let x=0; x<a; x++) {
            for (let y=0; y<a; y++) {
                if ((x==0&&b>=y)||(y==0&&b>=x)) {
                    if (b>=Math.sqrt((x+1)**2+(y+1)**2)) peT++;
                    else if (b>=x||b>=y) paT++;
                }
                else if (b>=Math.sqrt((x+1)**2+(y+1)**2)) peT++;
                else if (b>=Math.sqrt(x**2+y**2)) paT++;
            }
        }
    }
    
    return [peT, paT]
}

けっこう簡潔に書けたような気がする。
三平方の定理が当てはめられない、x軸,y軸いずれかが0のパターンを分けたところはちょっと冗長だった。なんとかならんもんか。

すごいかいとう

function countingTiles(radius) {
  var d = (x, y) => Math.sqrt(x * x + y * y),
      a = Math.ceil(radius), i = 0, x, y, f = 0, p = 0;
  while (i < a * a)
    d((x = i % a) + 1, (y = ~~(i++/a))+1) <= radius ? f++ : d(x, y) <= radius &&  p++
  return [4 * f, 4 * p];
}

例の如く何がどうなってるのか全くわからない。

2-3行目では変数をいくつか定義していて、
d...そのポイントの中心からの距離を２つの引数から計算。
a...半径の値を切り上げた数値を格納。
i...~~わからん。~~カウンタ的な？
x...~~わからん。~~そのタイルの右下位置のx座標
y...~~わからん。~~そのタイルの右下位置のy座標
f...完全な方のタイル。
p...部分的な方のタイル。

5-6行目のwhileブロックだけで90度分の円の中のタイルを数えているみたいだけど・・・
まず三項演算子の一つ目の式。

d((x = i % a) + 1, (y = ~~(i++/a))+1) <= radius ?

むむ、例えばradius=1.6, a=2として考えてみると、
1週目...i=0
d(0+1, 0+1) <= 1.6 ? //左上位置が[1,1]のタイル
2週目...i=1
d(1+1, 0+1) <= 1.6 ? //左上位置が[2,1]のタイル
3週目...i=2
d(0+1, 1+1) <= 1.6 ? //左上位置が[1,2]のタイル
4週目...i=3
d(1+1, 1+1) <= 1.6 ? //左上位置が[2,2]のタイル

なるほど確かに完全タイルを一つずつ順に見ていっている・・・・

上記の式が真にならない場合は次を実行

d(x, y) <= radius &&  p++

これは論理演算子の動き方でみたやつだ！
参考：JavaScriptの「&&」「||」について盛大に勘違いをしていた件 - Qiita

右下位置が最初の式のx,yで定義されているので、それをd()に代入して、半径より短い場合はp++を実行する。
すごいなー

学び

~~number

• numberの小数点部分を切り捨てる。numberが負の数値の場合はMath.floorと働きが違って、ただ小数点以下をなくすして整数部分を返すだけ。
  (参考：JavaScriptで小数を整数にするマニアックな方法とその実行速度 - q-az)

Math.floor(number)

• numberの小数点以下を切り捨てる。numberが負の値であれば整数部分が1下がる。
  例) Math.floor(-4.25)...-5

%(剰余算)

• 左のオペランドを右のオペランドで割った余りの数値を返す。左のオペランドの方が小さい場合は左のオペランドをそのまま返す。

++aとa++の違い

• どちらもincrementするすることには変わりはないが、前置と後置という考え方の違いがあって、具体的な違いとしては、これらを他の変数に代入する場合に、incrementするタイミングが変わる。前置は代入する前にa+1をし、後置はaを他の変数に代入したあとで、aを+1する。厳密に言えば、行を実行する前に加算をするかどうかという違い。
  参考：前置と後置 - ajaxtower,
  参考：JavaScript(2) 前置演算子と後置演算子 - ゆっくりいこう寅日記

反省

圧倒的センスを感じた。
あと、前置後置とか論理演算子とか細かい仕様を見落とさずに勉強していく。