ポエムです。
TL;DR
- 静的単一代入形式を「ループまで」拡張したらとても強力になったよ!
静的単一代入とは
詳しい説明は Wikipedia に譲ります。JavaScriptで言えば、すべてがconstで表現されている ようなものです。
さてこの静的単一代入、このままでは部分的な最適化に用いられる程度でしかありませんが、これをループまで拡張し、あらゆるプログラムを表現できるととても良いのではないのだろうか。というのが、本稿の内容です。
下記の疑似コードをご覧ください。
sum = 0
for x in xs {
sum = sum + x
}
これは、変数 sum を上書きしながらループを回す、一般的な手続き型言語のコードです。
これに対して、sum を上書きしないような以下の疑似コードを考えます。
for sum from 0; x in xs {
sum = last sum + x
}
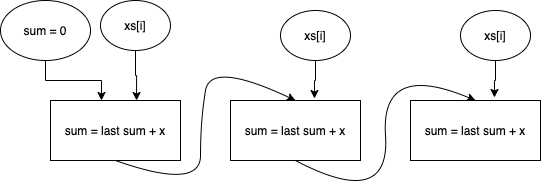
last sum の部分に注目してください。ここで last sum は前のループの同名変数を表します。sum へは一度のループで一回しか代入できません。各ループのsumはあくまで別の変数であり、lastを用いて他の(前の)ループでの値を参照できます。
これで晴れて、静的単一代入のルール「各変数が一度のみ代入される」を守りつつ、ループまで拡張することができました。
どう嬉しいのか
先述のsumの例では、各ループは前のループの計算結果を待たないと今回のループで計算ができないことが明確に表されました。図にするとこのような形です。
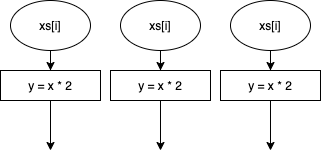
一方で、前のループの計算結果に依存しないことも明確に表すことができます。
for x in xs {
y = x * 2
}
last 演算子を使っていないので、各ループは完全に独立に計算ができます。
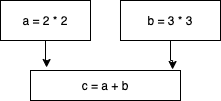
嬉しいのは、並列化を効かせやすい点です(たとえば、SIMD命令 のような)。この性質はループに限りません。以下の疑似コードを考えます。
a = 2 * 2
b = 3 * 3
c = a + b
c を求めるには a と b が必要ですが、aとbはお互いに独立して計算できます。つまり、並列に実行できます。
これは上述のようなシンプルな計算だけでなく、非常に重い計算でも同じことがいえます。I/Oなど長い待ちが発生する処理をa側に逃し、裏で出来る計算をb側で行う、のような表現も可能です。
静的単一代入の本来の目的がそうであるように、この形式に沿ってプログラムを書くことで、多様な最適化の恩恵が受けられます。
筆者はこの静的単一代入形式の拡張こそが、様々な計算モデルの中で最も適切に抽象化された形ではないかと考えています。
拙い文章ではありますが、以上が今回書きたかったポエムとなります。当然賢明な読者の方においては、ツッコミどころが多数あることかと思います。是非コメント欄にて議論を交わしませんか? いつまでもお待ちしております。