Go to Qiita Advent Calendar 2024 Top
LoginSignup
14
8

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@eigs(michio)

【MATLAB & Python】最適化計算と Google Sheets の読み書き

Last updated at Posted at 2019-09-15

やったこと

MATLAB から Python の呼び出し。具体的には

  1. Google Sheets からデータ読み込み (by Python)
  2. 最適化計算 （by MATLAB）
  3. Google Sheets へ結果の書き込み (by Python)

MATLAB でやるには手間がかかりそうだった Google Sheets との絡み（1と3）を、今回は MATLAB から Python モジュールを呼び出す方法で手抜きしました。

例えば


pyOut = py.gspread_sample.getValues();

こんな感じ。

誰向けの内容？

  • ちょっと Python でもかじっておくか・・という MATLAB ユーザー
  • 使いたい Python のモジュールがある MATLAB ユーザー
  • 使いたい MATLAB の関数がある Python ユーザー

向けかと思います。
Python と MATLAB連携についての公式ページはこちら：MATLAB からの Python 機能へのアクセス

なんで MATLAB と Python ？

全部 MATLAB で、または Python でやる、という選択肢ももちろんありますが、

  • Google Sheets を読み書きする Python コードを見つけた
  • MATLAB は得意という個人的な事情（笑）

の２つの理由から、MATLAB をベースにやってみることにしました。
Python は普段触らないので至らない点があるとは思いますが、もし改善できる点があれば優しくご指摘頂けると嬉しいです。

補足) File Exchange で公開されている MATLAB の関数 GetGoogleSpreadsheet を使ってもいいかもしれません。

環境

MATLAB R2019a (+ Optimization Toolbox)
Python 3.6
pip 19.2.3
gspread 3.1.0 → GitHub: gspread
oauth2client 4.1.3

参考にした Qiita 記事

Google Sheets とのデータのやり取りについては、以下をほぼそのまま使わせて頂きました。ありがとうございます！

で、実際何をやったのか

バランスが崩れた保有割合を目標割合に近づけるためには各銘柄を何株買えばいいのか、
そんな計算をする機能を作ってみました。リバランス重要ですからね（笑）
参考：ポートフォリオのリバランス：効果を計算してみた（株価取得編）

保有銘柄の株価や保有数などは Google Sheets で管理しているテイで
計算結果も Google Sheets 上に反映させます。

成果物はこちら（Google Sheets 上のキャプチャ）
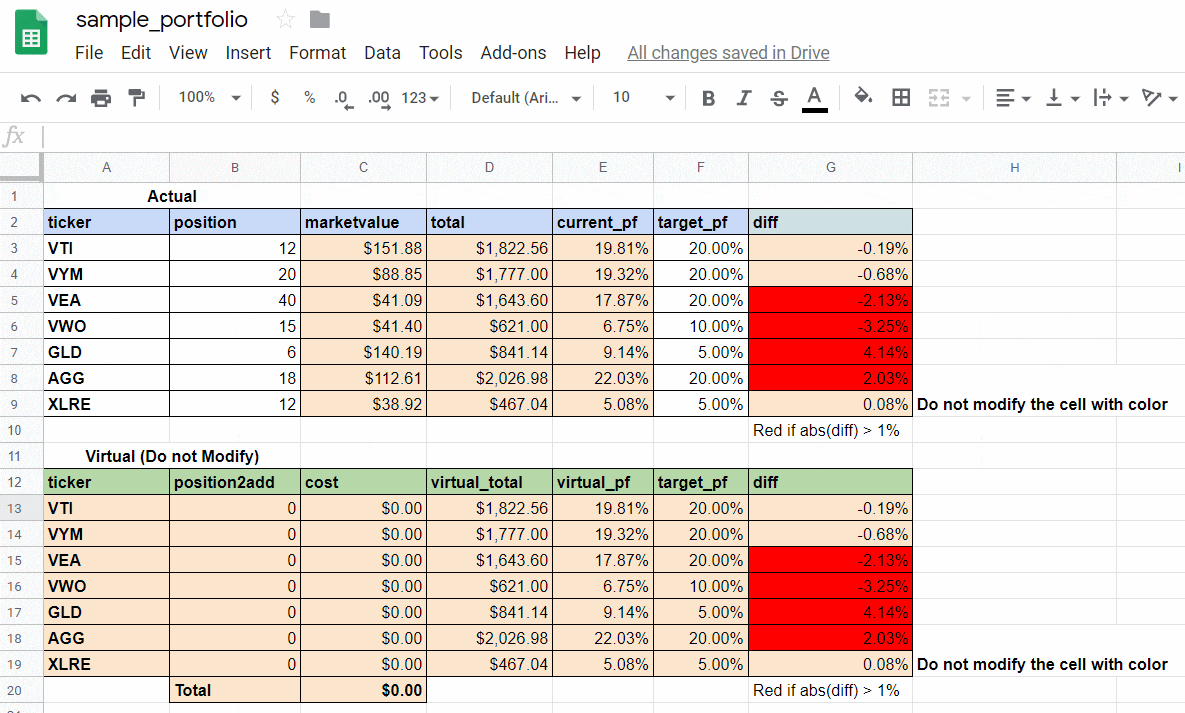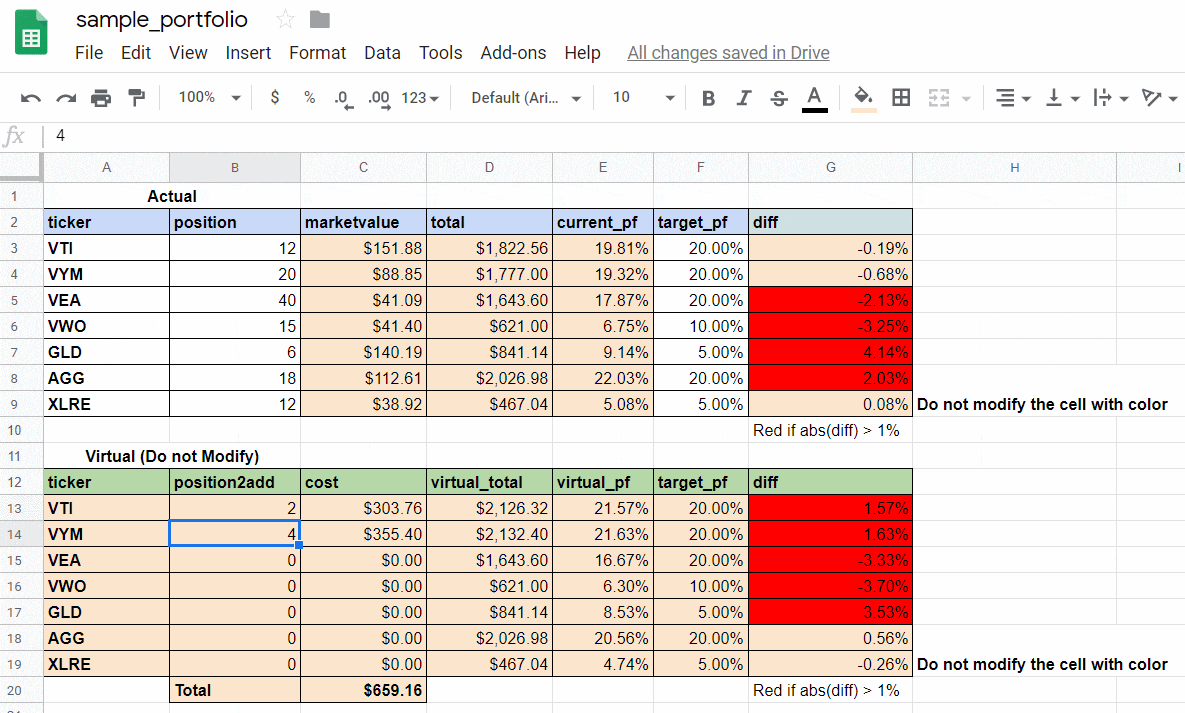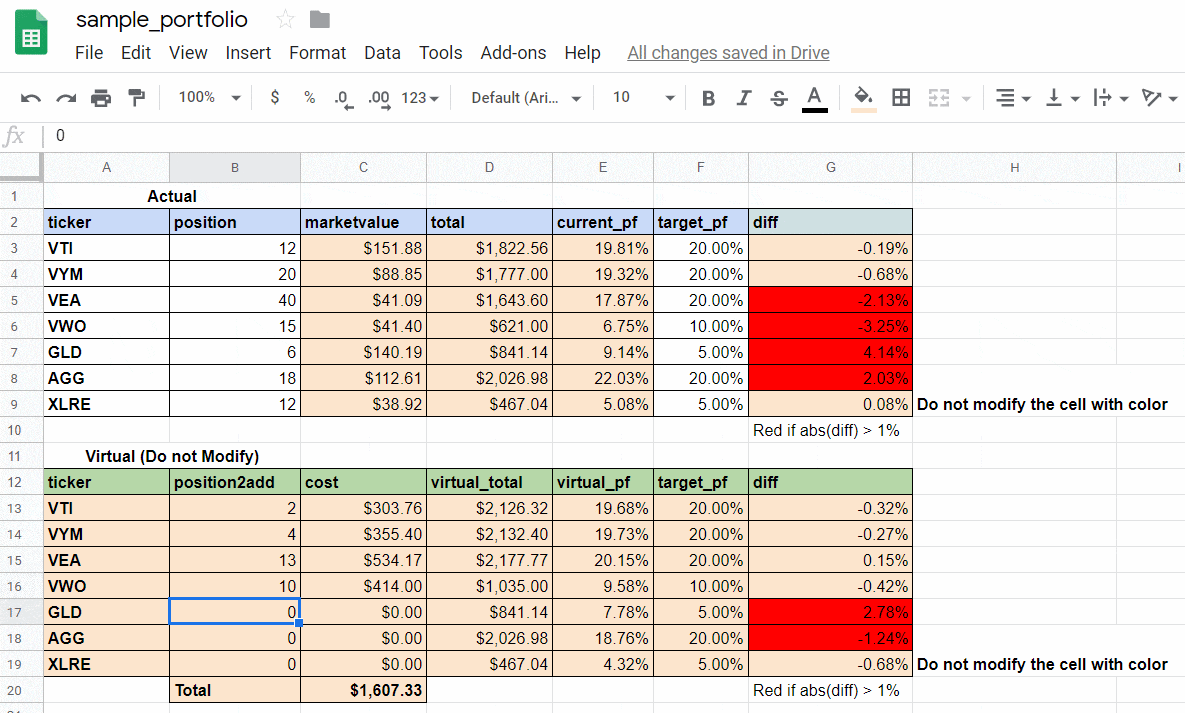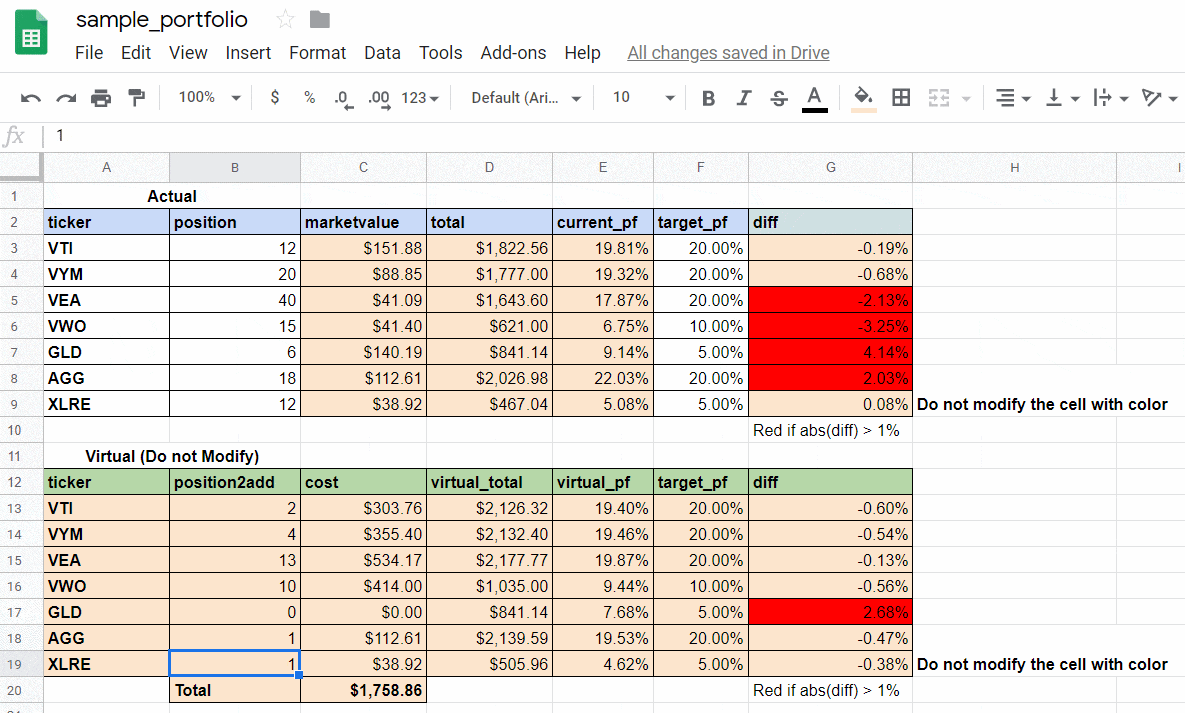
animation_samplegspread.gif

  • 上の表：現保有数
    • current_pf（現在保有割合）と target_pf（目標保有割合）の差が 1% 以上の銘柄を赤く表示しています。
  • 下の表：コードを実行した結果
    • 買い付けにかかる総額に上限を設けて、target_pf に近づけるための各銘柄の追加購入数をアップデートしています。次の買い付けはこれでいこう！

Sheet はこちら（sample_portfolio）で公開していますので、興味のある方はどうぞ。
ちなみに株価は Google Sheets の GOOGLEFINANCE 関数で取得してます。

順番に見ていきます。

1. Google Sheets からデータ読み込み (by Python from MATLAB)

必要なモジュールは gspread_sample.py (ページ下部に全文あり) に纏めています。
MATLAB からの呼び出し方はシンプルです。事前の load は不要。

% getValues 関数（Python）を使って
% Google Spreadsheet からデータ読み込み（py.tuple クラスとして）
pyOut = py.gspread_sample.getValues();
whos pyOut

すると 出力は tuple として得られます。

Name       Size            Bytes  Class       Attributes

pyOut      1x2                 8  py.tuple

このデータ型だとこの後使う fmincon 関数に引数として使えないので、ごにょごにょ処理していきます。特に Google Sheets の値が全部文字列として入ってきてしまっている部分などはPython 側で処置してもいいですが、いかんせん MATLAB の方が得意なので MATLAB でやります。

欲しいのは数値だけ。

% まずセル型に変更
vname = cell(pyOut{1}); % 変数名部分
value = cell(pyOut{2}); % データ部分

%% データを MATLAB で処理しやすいように変更
% データを string 型に変更
vname = cellfun(@(x) string(x.value), vname);
value = cellfun(@(x) string(x.value), value);
value = reshape(value,6,[])';
% table 型変数に纏めておく
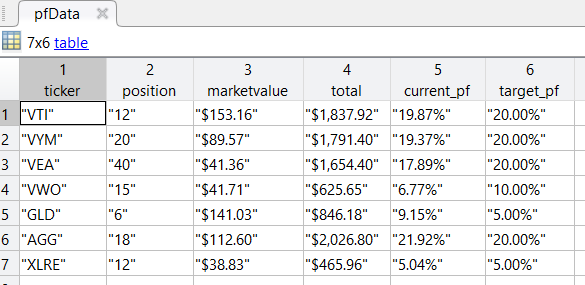
pfData = array2table(value,'VariableNames',vname)

この時点でようやくこんな感じ。$ や % が邪魔ですね。

pfData1.PNG


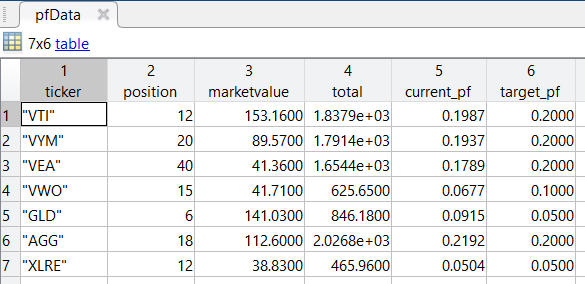
%% さらに細かい各種処理
pfData.position = double(pfData.position);% string -> double 
pfData.marketvalue = double(extractAfter(pfData.marketvalue,"$")); % $マーク削除して double に
pfData.total = double(extractAfter(pfData.total,"$")); % $マーク削除して double に
pfData.current_pf = double(extractBefore(pfData.current_pf,"%"))/100; % %削除
pfData.target_pf = double(extractBefore(pfData.target_pf,"%"))/100; % %削除

やっとすっきり。Python 側で前処理できていればもう少し簡単なのかな？

pfData2.PNG

2. MATLAB で最適化計算（by MATLAB）

さて、最適な購入株数を求めましょう。
今回は制約条件（購入予算 Cost）も使いたいので Optimization Toolbox の fmincon を使用します。詳細はコメントを参照ください。制約条件がなければ Toolbox いらずの fminsearch でもいいですね。

%% 最適化に入ります
% それぞれの銘柄いくつ購入すればターゲットとする保有割合に近づくかを求めます。
% その際の制約は Cost：合計何ドルまでの購入とするか
% ここでは 2k (約 20万円）とします。
Cost = 2e3; % $2k

% fmincon を使用
% 本来は整数問題ですが実数で株数を求めた後、端数は無視します。
% 購入株数が多ければそこまで問題にはならないため。
% もちろん購入株数が少ない場合は影響があるため調整は行っているみたいですが、
% この方法はロボアドバイザー THEO も同じ（要引用）
% 線形不等式制約（合計コストが Cost 以下）
A = pfData.marketvalue'; 
b = Cost;
% 線形等式制約はなし
Aeq = [];
beq = [];
% 購入数の上下限
lb = zeros(7,1);
ub = inf(7,1);
% 初期値は 0。
x0 = zeros(7,1);

% 目的関数は getDiff で定義されています。
% ターゲットの保有割合との誤差二乗和平方根を最小とすることを目指します。
x = fmincon(@(x) getDiff(pfData,x),x0,A,b,Aeq,beq,lb,ub);

目的関数に指定した getDiff.m は以下の通り。追加購入後の割合の、それぞれの目標割合との差、の２乗、の和、の平方根です。ややこしい！

getDiff.m
function errorRMS = getDiff(pfData, position2add)
newTotal = pfData.marketvalue.*(position2add+pfData.position);
newPF = newTotal/sum(newTotal);
errorRMS = sqrt(sum( (newPF - pfData.target_pf).^2 ) );
end

3. Google Sheets へ結果の書き込み (by Python from MATLAB)

fmincon の実行の結果、追加すべき株数は

x =

    2.3795
    4.5881
   13.2482
   10.8342
    0.0000
    1.5591
    1.2656

と求まりますので、えいや！と小数点以下は切り捨てて、Google Sheets に書き込みます。
余ったキャッシュは MMF でも購入しておきましょう。

% 購入株数の小数点以下切り捨て
xlong = floor(x);

% updateValues 関数（Python）を使って
% Google Spreadsheet へデータの書き込み
py.gspread_sample.updateValues(xlong)

以上！

まとめ

MATLAB と Python を連携させてみました。データ型の行き来が多少面倒くさい部分もありますが、

py.gspread_sample.getValues

と気軽に呼べるのは便利でした。Python ももう少し勉強しておくと活動範囲が広がりそう！

多少手間取ったのは、Python 側のコードの編集を MATLAB 側での実行に反映させるには、モジュールの再読み込みが必要だったところ。

clear classes %#ok<CLCLS>
mod = py.importlib.import_module('gspread_sample');
py.importlib.reload(mod);

と冒頭に付けておけばとりあえず安心です。
詳細はこちらにありました：変更されたユーザー定義 Python モジュールの再読み込み

以下に今回使用した Python, MATLAB コード全文を記載しておきます。

Python 関数全文

gspread_sample.py
# gspread_sample.py
def getValues():
    """get values in A2:F9 from 'sample_portfolio'"""

    import gspread
    from oauth2client.service_account import ServiceAccountCredentials

    scope = ['https://spreadsheets.google.com/feeds',
             'https://www.googleapis.com/auth/drive']

    credentials = ServiceAccountCredentials.from_json_keyfile_name('<JSONファイル名>.json', scope)
    gc = gspread.authorize(credentials)
    wks = gc.open('sample_portfolio').sheet1

    vname_list = wks.range('A2:F2');
    value_list = wks.range('A3:F9');
    #print(vname_list)

    return vname_list, value_list


def updateValues(position2add):
    """updates values in B13:B19 on 'sample_portfolio' with virtual purchase"""

    import gspread
    from oauth2client.service_account import ServiceAccountCredentials

    scope = ['https://spreadsheets.google.com/feeds',
             'https://www.googleapis.com/auth/drive']

    credentials = ServiceAccountCredentials.from_json_keyfile_name('<JSONファイル名>.json', scope)
    gc = gspread.authorize(credentials)
    wks = gc.open('sample_portfolio').sheet1

    # Update in batch
    cell_list = wks.range('B13:B19')

    for x in range(7):
       cell_list[x].value = position2add[x]

    wks.update_cells(cell_list)

    # Update one cell by one
    """
    wks.update_acell('B13', position2add[0])
    wks.update_acell('B14', position2add[1])
    wks.update_acell('B15', position2add[2])
    wks.update_acell('B16', position2add[3])
    wks.update_acell('B17', position2add[4])
    wks.update_acell('B18', position2add[5])
    wks.update_acell('B19', position2add[6])
    """

def main():
    vname_list, value_list = getValues()
    print(vname_list)
    print(value_list)

if __name__ == '__main__':
    main()

MATLAB コード全文（再掲）

sample_optimization.m
% 変更されたユーザー定義 Python モジュールの再読み込み
% https://www.mathworks.com/help/matlab/matlab_external/call-modified-python-module.html
clear classes %#ok<CLCLS>
mod = py.importlib.import_module('gspread_sample');
py.importlib.reload(mod);

% getValues 関数（Python）を使って
% Google Spreadsheet からデータ読み込み（py.tuple クラスとして）
pyOut = py.gspread_sample.getValues();
whos pyOut 
% セル型に変更
vname = cell(pyOut{1}); % 変数名部分
value = cell(pyOut{2}); % データ部分

%% データを MATLAB で処理しやすいように変更
% データを string 型に変更
vname = cellfun(@(x) string(x.value), vname);
value = cellfun(@(x) string(x.value), value);
value = reshape(value,6,[])';
% table 型変数に纏めておく
pfData = array2table(value,'VariableNames',vname)

%% さらに細かい各種処理
pfData.position = double(pfData.position);% string -> double 
pfData.marketvalue = double(extractAfter(pfData.marketvalue,"$")); % $マーク削除して double に
pfData.total = double(extractAfter(pfData.total,"$")); % $マーク削除して double に
pfData.current_pf = double(extractBefore(pfData.current_pf,"%"))/100; % %削除
pfData.target_pf = double(extractBefore(pfData.target_pf,"%"))/100; % %削除
% 完成
pfData

%% 最適化に入ります
% それぞれの銘柄いくつ購入すればターゲットとする保有割合に近づくかを求めます。
% その際の制約は Cost：合計何ドルまでの購入とするか
% ここでは 2k (約 20万円）とします。
Cost = 2e3; % $2k

% fmincon を使用
% 本来は整数問題ですが実数で株数を求めた後、端数は無視します。
% 購入株数が多ければそこまで問題にはならないため。
% もちろん購入株数が少ない場合は影響があるため調整は行っているみたいですが、
% この方法はロボアドバイザー THEO も同じ（要引用）
% 線形不等式制約（合計コストが Cost 以下）
A = pfData.marketvalue'; 
b = Cost;
% 線形等式制約はなし
Aeq = [];
beq = [];
% 購入数の上下限
lb = zeros(7,1);
ub = inf(7,1);
% 初期値は 0。
x0 = zeros(7,1);

% 目的関数は getDiff で定義されています。
% ターゲットの保有割合との誤差二乗和平方根を最小とすることを目指します。
x = fmincon(@(x) getDiff(pfData,x),x0,A,b,Aeq,beq,lb,ub);

% 購入株数の小数点以下切り捨て
xlong = floor(x);

% updateValues 関数（Python）を使って
% Google Spreadsheet へデータの書き込み
py.gspread_sample.updateValues(xlong)

% 購入後の新しい保有数(チェック用)
% position2 = pfData.position + xlong;
% total = pfData.marketvalue'*position2;
% [pfData.current_pf,pfData.marketvalue.*position2/total,pfData.target_pf]


function errorRMS = getDiff(pfData, position2add)
newTotal = pfData.marketvalue.*(position2add+pfData.position);
newPF = newTotal/sum(newTotal);
errorRMS = sqrt(sum( (newPF - pfData.target_pf).^2 ) );
end
14
8
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
14
8

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?