機械学習 回帰問題の評価方法（平均二乗誤差と決定係数）

○この記事の要点
回帰問題の評価方法について学習したのでメモ。

#○ソースコード(Python)：線形回帰モデルの場合

回帰問題の学習と評価

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
from sklearn.svm import SVR
%matplotlib inline

# データ準備。ボストンの住宅価格
data = load_boston()
X = data.data[:, [5,]] # 説明変数として、部屋数だけを抽出
y = data.target

# 単回帰モデルでの学習
model_l = LinearRegression()
model_l.fit(X, y)
# 回帰直線y=ax + bの傾きと切片の値
print(model_l.coef_) # a：傾き
print(model_l.intercept_) #b：切片

# 予測
l_pred = model_l.predict(X)

# グラフ表示
fig, ax = plt.subplots()
ax.scatter(X, y, color='red', marker='s', label='data')
ax.plot(X, l_pred, color='blue', label='regression curve')
ax.legend()
plt.show()

結果
[9.10210898]
-34.67062077643857

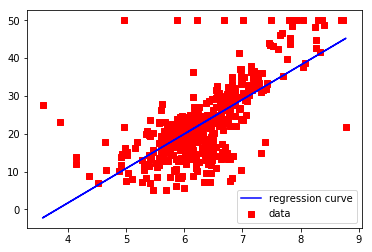
それなりな感じ？

平均二乗誤差

予測値と実際の値の誤差二乗をすべて計算し、その平均をとったもの。小さいほど予測値が正しい。
※予測する値が大きい場合、相対的に値が大きくなるので、異なる値を比較する場合は単純に大きい／小さいと判断ができない。

平均二乗誤差

mean_squared_error(y, l_pred)
43.60055177116956

決定係数

平均二乗誤差を使って予測の正確さを示す数値。0～1の値になる。異なる値を比較する場合にも相対的に比較できる値となる。

決定係数

r2_score(y, l_pred)
0.48352545599133423

線形回帰モデルの結果が良い結果なのか。次は他のアルゴリズムも試してみる。
#○ソースコード(Python)：SVRモデルの場合

SVRの学習と評価

# SVR(サポートベクトルマシン（カーネル法）)での学習
model_s = SVR(C=0.01, kernel='linear') # 正則化パラメータが0.01で線形カーネルを使用
model_s.fit(X, y)

# 回帰直線y=ax + bの傾きと切片の値
print(model_s.coef_) # a：傾き
print(model_s.intercept_) #b：切片

# 予測
s_pred = model_s.predict(X)

# グラフ表示
fig, ax = plt.subplots()
ax.scatter(X, y, color='red', marker='s', label='data')
ax.plot(X, l_pred, color='blue', label='regression curve')
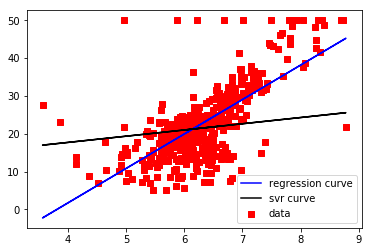
ax.plot(X, s_pred, color='black', label='svr curve')
ax.legend()
plt.show()

結果
[[1.64398]]
[11.13520958]

SVRの方が微妙？？

平均二乗誤差と決定係数

mean_squared_error(y, s_pred)
72.14197118147209
r2_score(y, s_pred)
0.14543531775956597

線形回帰の方が優秀。ただし！！SVRのハイパーパラメータ（正則化パラメータやカーネル手法）を変更するとわからない。

#○ソースコード(Python)：SVRモデルの場合

SVRの学習と評価（ハイパーパラメータを変える）

model_s2 = SVR(C=1.0, kernel='rbf') # 正則化パラメータが1でrbfカーネルを使用
model_s2.fit(X, y)

# 予測
s_pred2 = model_s2.predict(X)

# グラフ表示
fig, ax = plt.subplots()
ax.scatter(X, y, color='red', marker='s', label='data')
ax.plot(X, l_pred, color='blue', label='regression curve')
ax.plot(X, s_pred, color='black', label='svr curve')
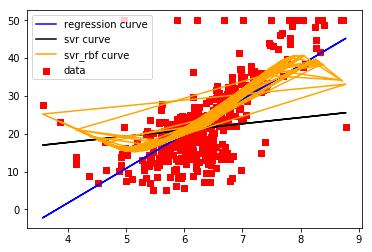
ax.plot(X, s_pred2, color='orange', label='svr_rbf curve')
ax.legend()
plt.show()

結果

なめらかでいい感じ？？

平均二乗誤差と決定係数

mean_squared_error(y, s_pred2)
37.40032481992347
r2_score(y, s_pred2)
0.5569708427424378

線形回帰よりも優秀。ハイパーパラメータ次第ということ。

■感想
・回帰問題の評価方法について勉強。平均二乗誤差も決定係数も「予測値と実データの差」を元に良し悪しを決めている。プログラムとしては、「正解データのリスト」と「予測データのリスト」を比較してそれぞれのデータで差を出して二乗して平均出してる。感覚的にわかりやすい。