Ceres Solverを使って歪んだ“多面体”を構築する #最適化

昔作ったやつをCeres Solverを使ったらいい感じにできないかなと思って作りました．

こんな感じの“多面体”が得られるようなプログラムです．

より多くの結果をこちらで見られます．
リポジトリはこちら

背景

今回対象にしたのは，東大の藤田誠教授・藤田大士研究員のグループから発表された論文¹で錯体分子から見出された4価のGoldberg多面体です．

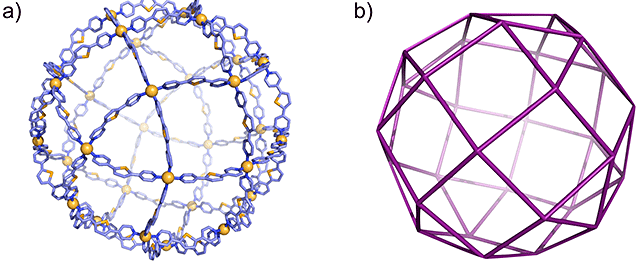
（https://www.jst.go.jp/pr/announce/20161222/index.html より引用）

Goldberg多面体は元々，数学者であるM. Goldberg先生によって提案された，やはりいわゆる多面体ではない歪んだ“多面体”ともいうべき存在で，面に歪みを許容することで半正多面体の概念を拡張したようなものです．
詳しくは https://en.wikipedia.org/wiki/Goldberg_polyhedron を参照のこと（数学は専門でないのでWikipediaでご容赦を）．

オリジナルのGoldberg多面体は歪んだ五角形と六角形の面から構成されたものですが，論文¹では歪んだ三角形と四角形の面から構成されたGoldberg多面体に類したような“多面体”（論文¹が呼んでいるtetravalent Goldberg polyhedraを和訳して，以降4価のGoldberg多面体と呼ぶ）が，錯体分子の構造から見出されました．
単結晶X線構造解析という単結晶にX線を当てることで，原子の配置がわかるようになる手法があり，それを使って構造を求めているので文字通り見出されています．

論文¹についての詳細は以下参照．

https://www.nature.com/articles/nature20771
- 元論文．Natureなので有料です
https://www.jst.go.jp/pr/announce/20161222/index.html
- 東大のプレス
https://www.chem-station.com/blog/2016/12/Goldberg.html
- （有機）化学界隈では有名なサイト

4価のGoldberg多面体は，表面上で最も近い三角形同士の位置関係を示すようなh, kという特徴量で表され，これらの値を大きくしていくことで無数に異なる4価のGoldberg多面体を作っていくことができます．

ということで，h, kを外から与えて，当てはまる4価のGoldberg多面体の頂点座標を出力するプログラムを作成しました．

実装

このプログラミングは2年半前くらいにRubyで適当山登り法を使って実装していました．
ただ，ただでさえRubyという決して速くはない言語なのにアルゴリズムが適当過ぎて，動作が無茶苦茶遅いという問題がありました．

当時はプログラミング初めて数か月で最適化のさの字も知らなかったが，今では少しはわかるようになったし，Ceres Solver（Google製の非線形最小二乗法ソルバ）の存在も知っている．ということで，Ceres Solverを使って書き直してみたということになります．

パラメータ

少々強すぎるとは思いますが，各頂点は単位球上にあるという仮定を置き，頂点を球座標系で $\theta, \phi$ を用いて表すことにしました．
さらに，4価のGoldberg多面体はC4対称軸（その軸に関して90度回転しても同じになるようなもの）が3本あるので，それを表すために一部の点は自身のパラメータを持たず，C4対称性を保つように決めたある別の点に原点中心の回転を施すことにより座標を定めています．

コスト関数

まずは，各辺の長さができるだけ近い値になって欲しいので，そうなるように，各辺の平均値との差の自乗和をコスト関数としました．
$$
\begin{align}
s_i &= (辺iの長さ) \\
N_s &= (辺の数) \\
\mathcal L_s &= \sum_i^{N_s}\left(s_i-\frac{1}{n}\sum_j^{N_s}s_j\right)^2
\end{align}
$$

ただこれだけだと，四角形がひし形になりがちだったので，四角形の対角線に対するコストを加えました．

$$
\begin{align}
d_i &= (対角線iの長さ) \\
N_d &= (対角線の数) \\
\mathcal L_d &= \sum_i^{N_d}\left(\frac{d_i}{\sqrt 2}-\frac{1}{n}\sum_j^{N_s}s_j\right)^2
\end{align}
$$

ということで，全体のコスト関数としては，以下のようになります． $\beta$ はハイパパラメータです．

$$
\mathcal L = \mathcal L_s + \beta\mathcal L_d
$$

グラフの構築

頂点をバラまいて適当に最適化したらいいんでしょ……，とそうは問屋が卸しません，
先のコスト関数を実現するためには，どの頂点同士が辺で結ばれているかを知っておかないといけないので，頂点をノード，辺をエッジとしたグラフを構築する必要が出てくることがわかります．

実は最適化フェーズよりこのグラフ構築が一番辛いし難しかったのですが，説明できる気がしないので割愛します．
簡単に言うと，必ず以下のように正方形が(h + k - 1) * (h + k -1)個並ぶものが6面あるので，それを使ってノードに連番を振っていて，重なり（赤線と桃線に注目）があったら適当にマージして，いろいろと頑張ります．

コスト関数の実装

全体としてはこんな感じです．

struct PolyhedronCostFunctor {
  explicit PolyhedronCostFunctor(std::shared_ptr<Polyhedron<double>> polyhedron) : polyhedron_(polyhedron) {}
  virtual ~PolyhedronCostFunctor() = default;

  bool operator()(double const* const* parameters, double* residual) const {
    polyhedron_->UpdateParams(parameters[0], parameters[1]);
    auto* cur_res = residual;
    for (auto it = polyhedron_->Edges().cbegin(); it < polyhedron_->Edges().cend(); ++it, ++cur_res) {
      *cur_res = it->Length() - polyhedron_->EdgeLengthMean();
    }
    for (auto it = polyhedron_->Diagonals().cbegin(); it < polyhedron_->Diagonals().cend(); ++it, ++cur_res) {
      *cur_res = kBeta * (it->Length() / std::sqrt(2.) - polyhedron_->EdgeLengthMean());
    }
    return true;
  }

  static auto Create(std::shared_ptr<Polyhedron<double>> polyhedron) {
    const auto abs_point_size = static_cast<int>(polyhedron->AbsPointSize());
    const auto residual_size = polyhedron->Edges().size() + polyhedron->Diagonals().size();

    auto cost_function =
        new ceres::DynamicNumericDiffCostFunction<PolyhedronCostFunctor>(new PolyhedronCostFunctor(polyhedron));
    cost_function->AddParameterBlock(abs_point_size);
    cost_function->AddParameterBlock(abs_point_size);
    cost_function->SetNumResiduals(static_cast<int>(residual_size));

    return cost_function;
  }

 private:
  // weight of cost to diagonal lenght
  static constexpr double kBeta = 0.7;

  std::shared_ptr<Polyhedron<double>> polyhedron_;
};

Ceres Solverを使うにはoperator()が定義してあるstructを定義する必要があります．
operator() はパラメータと残差のバッファを受け取り，その中で，受け取ったパラメータに対応する残差を格納してreturnするだけです．
先に述べたコスト関数をそのまま実装したのがこちらです．

  bool operator()(double const* const* parameters, double* residual) const {
    polyhedron_->UpdateParams(parameters[0], parameters[1]);
    auto* cur_res = residual;
    for (auto it = polyhedron_->Edges().cbegin(); it < polyhedron_->Edges().cend(); ++it, ++cur_res) {
      *cur_res = it->Length() - polyhedron_->EdgeLengthMean();
    }
    for (auto it = polyhedron_->Diagonals().cbegin(); it < polyhedron_->Diagonals().cend(); ++it, ++cur_res) {
      *cur_res = kBeta * (it->Length() / std::sqrt(2.) - polyhedron_->EdgeLengthMean());
    }
    return true;
  }

自動微分を使うにはdoubleではなく，Ceres Solverの独自型に対応する必要があり，それが大変そうだったので，単純に数値微分で済ませました．
h, kの値によって，残差の数もパラメータの数も変わるので， DynamicNumericDiffCostFunction で動的に設定します．AddParameterBlockを二回呼び出しているのは，それぞれ，$\theta, \phi$ 用です．

  static auto Create(std::shared_ptr<Polyhedron<double>> polyhedron) {
    const auto abs_point_size = static_cast<int>(polyhedron->AbsPointSize());
    const auto residual_size = polyhedron->Edges().size() + polyhedron->Diagonals().size();

    auto cost_function =
        new ceres::DynamicNumericDiffCostFunction<PolyhedronCostFunctor>(new PolyhedronCostFunctor(polyhedron));
    cost_function->AddParameterBlock(abs_point_size);
    cost_function->AddParameterBlock(abs_point_size);
    cost_function->SetNumResiduals(static_cast<int>(residual_size));

    return cost_function;
  }

あとはCeres Solver共通なので割愛

結果

https://eduidl.github.io/polyhedron を見て頂ければわかる通り何となくできている感じがします．
また目的の一つであった，動作の高速化もできたっぽく，より大きなh, kにも耐えうるようになりました．

“Self-assembly of tetravalent Goldberg polyhedra from 144 small components”, Fujita, D.; Ueda, Y.; Sato, S.; Mizuno, N.; Kumasaka, T.; Fujita, M. Nature 2016, 540, 563-566. doi:10.1038/nature20771 ↩