統計学を学びはじめる #2
Hi!
2回目データサイエンス活動、略して”デーかつ”。いっきまーす☆
本日の内容は、、、、、、
記述統計
⑴前回紹介した
大学4年間の統計学が10時間でざっと学べる(以降は”大学4年間”と略)
のP.75まで。
マセマなら講義6。
統計学基礎なら大体P.35ぐらい。
⑵目的は
各用語の整理、共分散(covariance)、標準偏差(S.D. or standard deviation)
盲点ついてくぜ
良し行くぞ
<<<用語の整理>>>
・記述統計(descriptive statistics)→データ集団の性質を統計的記述方法で理解する方法。
もう一個は推測統計(inferential statistics)っていって、母集団についての情報の推測をする。
!「母集団」=「データの元集団」
⇒つまり、
[記述統計:データの特徴を理解]⇔[推測統計:データの母集団について考察]
一般的に世間で言われる「統計~調査」とかは推測統計のことをさすことが多い。
・データ
観測とかして数値的なデータ→量的データ
属性、項目、カテゴリー→質的データ
の2種類
・名義尺度、順序尺度、間隔尺度、比尺度 とかってあるんだけど重要なのは、比尺度には原点があるということ。
名義尺度、順序尺度が質的変量で、間隔尺度、比尺度が量的変量。
・量的データを表現するのにあたって、"度数分布表"と"ヒストグラム"は超重要。
・平均(mean)
\overline {x}=\dfrac {1}{n}\sum ^{n}_{i=1}x_{i}
・平均からの偏差(deviation:平均からどんだけ離れてるか)を分散(variance)っていう
s^{2}=\dfrac {1}{n}\sum ^{n}_{i=1}\left( x_{i}-\overline {x}\right)^{2} = \dfrac {1}{n}\sum ^{n}_{i=1}x^{2}_{i} - \overline{x}^{2}
こうすることで、データがどのくらいの割合で分布しているか見れる。"右端の式は今後よく出てくるから覚えておくように!"計算はマセマのP.145よんでね。
分散の値のままだと、次元(単位)が2乗のまんまだから、平方根をとって標準偏差(S.D.)とする
S.D=s=\sqrt {s^{2}}=\sqrt {\dfrac {1}{n}\sum ^{n}_{i=1}\left( x_{i}-\overline {x}\right) ^{2}}
こうすりゃ、元データとの単位もあいますと。
・メディアンはデータを大きさ順に並べた時、中間の位置にある値。
・モードは最頻値のことで、要は度数の一番高いやつ
ヒストグラムる
まずはExcelでつくってみる
こんなデータがありますと。
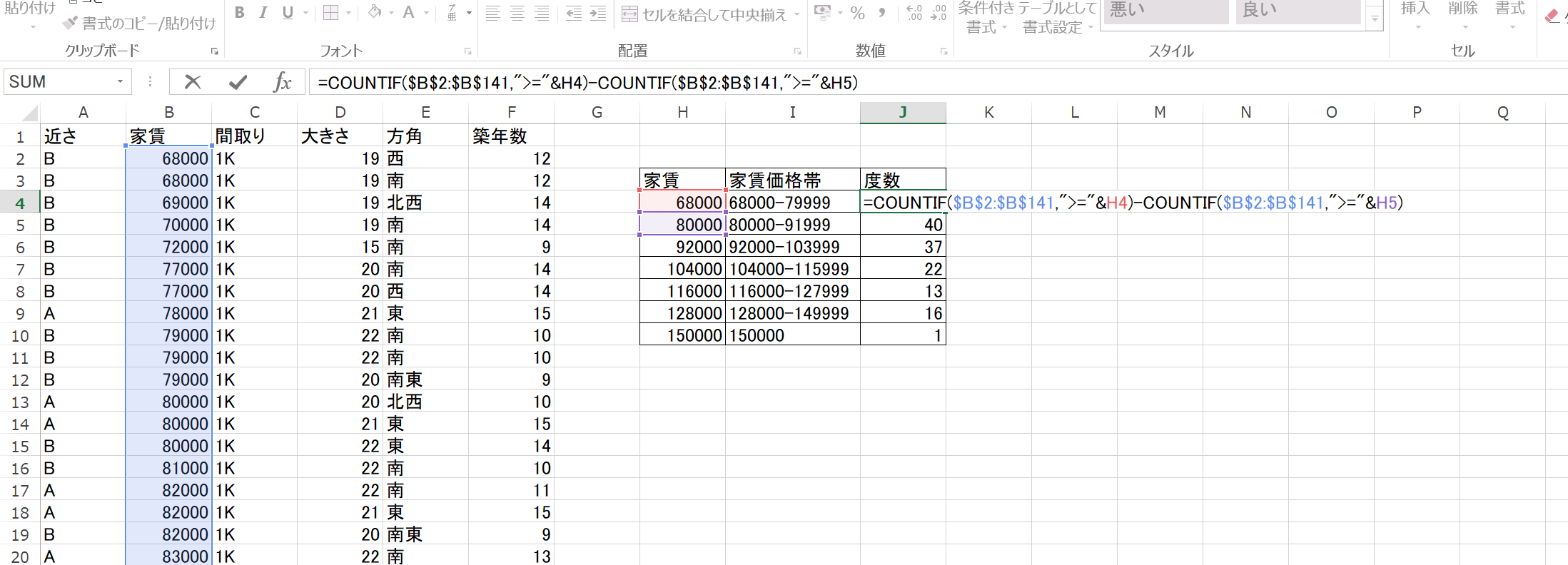
度数分布表は最大値(MAX)と最小値(min)の間をいくつかの階級(class)に分けて、それぞれの階級に含まれる度数(frequency)をカウント。
今回はMAXが150000で、minが68000。俺の家賃は最小値笑
度数分布表ができまして、
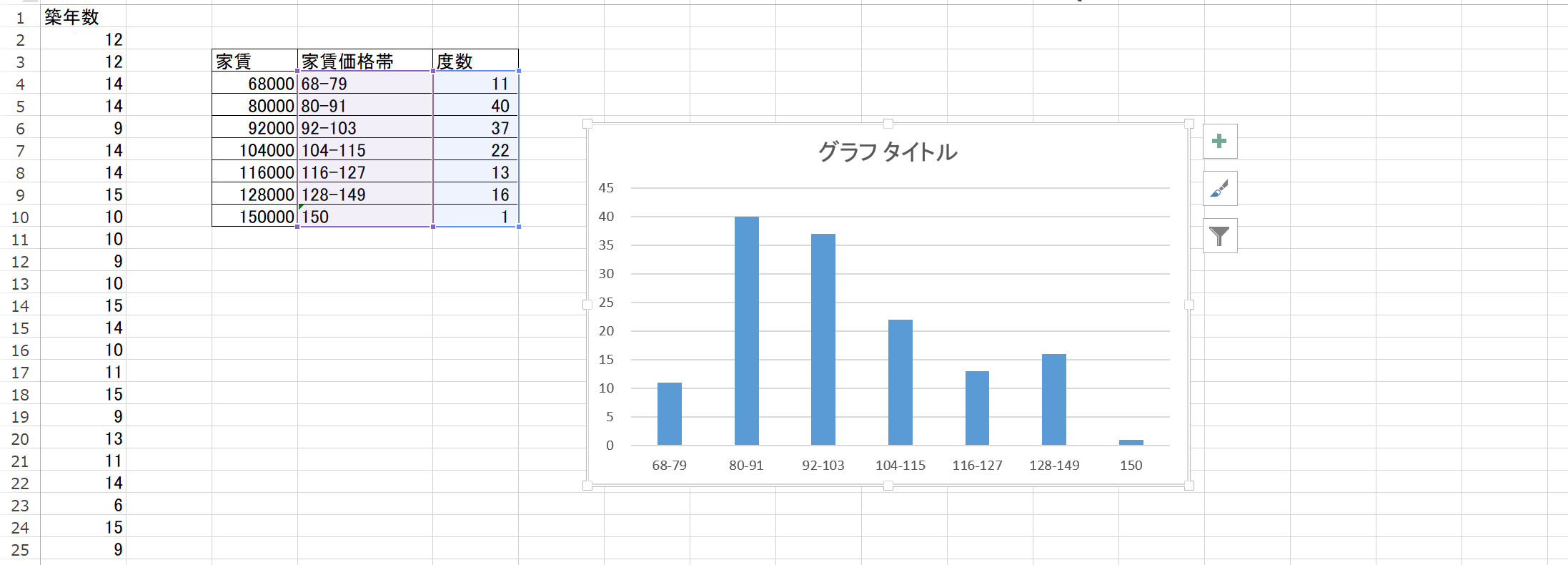
ヒストグラムがこんな感じ。
こういう基礎は、後々習えなくなるもんだから、今のうちに習熟しておこうね。
次回はいよいよ、最小二乗法!!
乞うご期待!
Go Beyond the limits