このブログis何
Googleが開発したOR-Toolsを使って数理最適化を学んでいきます。
内容は殆どがこの本を参考にしたものです。
Practical Python AI Projects: Mathematical Models of Optimization Problems with Google OR-Tools (English Edition)
著者によるコード一覧はこちら
本ブログに記載するコードは著者オリジナルの物と殆ど変わらず、一部日本語に直したりしている程度です。
数学的な厳密さや、理論の解説は優先度低めになってます。ご勘弁を。
今回は : 線形計画~プロジェクトマネジメント編~
複数のタスクが存在し、それぞれに所要時間や先行タスクがある時、最短で終わらせる方法を求めます。
場面設定
たかし君は自粛期間で暇なので料理に挑戦することにしました。ちなみに筆者は料理ダメダメ人間なので適当なこと書いちゃってるかもしれません。
男子小学生らしくカレーライスを作ることにしたたかし君は、熟練のお母さんよりも速く作れるようになりたいと考えました。いくつか工程のあるカレーライスですが、どの工程をいつ始めれば料理時間が最短になるでしょうか?
ポイント
プロジェクトマネジメントの問題でポイントとなるのは、大きく
・各タスクの所要時間
・各タスクの先行タスク
の2つです。先行タスクとは、そのタスクを始める前に必ず完了していなければならないタスクのことです。カレーライスの例では、「肉と野菜を炒める」の先行タスクは、「肉と野菜を切る」、「フライパンにサラダ油をひく」となります。僕の知っているカレーライスではそうです。
この後の議論のために、少し話を一般化しておきます。
タスクの集合$T$があり、各要素には
・所要時間
・$T$の部分集合である先行タスク(空集合も可)
があります。例を下の表に示します。
| タスク | 所要時間 | 先行タスク |
|---|---|---|
| 0 | 3 | {} |
| 1 | 6 | {0} |
| 2 | 3 | {} |
| 3 | 2 | {2} |
| 4 | 2 | {123} |
| 5 | 7 | {} |
| 6 | 7 | {01} |
| 7 | 5 | {6} |
| 8 | 2 | {137} |
| 9 | 7 | {17} |
| 10 | 4 | {7} |
| 11 | 5 | {0} |
タスクが数字で無機質な感じがするので、適当に当てはめてみて下さい。カレーライスにしては工程が多すぎるかもしれませんね。恐らくインドカレーです。
定式化
それでは数式で表現してみましょう。
今回の例で決定変数となるのは、「どのタスクをいつ始めるか」です。先行タスクの制約を守りながらこの変数を上手く決めることで、最後のタスクが終わるまでの時間を最短にすることができます。
タスクの集合を$T$として、各タスクの開始時刻を以下のように定義します。
0 \leq t_i \quad \forall i \in T
上の表の例で言うと、$t_0 = 3$,$t_5=7$です。
先行タスクの制約を考慮するために、タスク$i$の所要時間$D_i$(表の2列目に対応)と、タスク$i$の先行タスクを表す部分集合$T_i \subset T$(表の3列目に対応)を用意しましょう。
これらを用いて、タスク$i$の開始時刻の下限制約を以下の式で表現します。
t_j + D_j \leq t_i \quad \forall j \in T_i ; \forall i \in T
例えばタスク7の先行タスクは6なので、$t_6 + D_6(=7) \leq t_7$が成り立つ必要があります。
しつこいようですが、今回の目的は、プロジェクト(ここではカレー作り)の完了までの時間を最小化することです。もし、各タスクが順番に行われるのであれば、(最後のタスク開始時刻+その所要時間)が該当します。
実際にはそうではなく、いくつかのタスクは平行して処理されるはずです。料理はこの平行処理の上手さでベテラン主婦との差が出ますからね、知らんけど。どのタスクが最後か分からなかったり、最後のタスクが1つでない場合はそうすればよいのでしょうか?
そこで、新しく変数$t$を導入します。この変数に対して、「任意のタスクの開始時刻+所要時間よりも大きい」という制約を設けます。
t_i + D_i \leq t \quad \forall i \in T
そして$t$を最小化することを目的にすれば、$t$はプロジェクトの完了時刻になります。
実装
今回の例題を解くためのコードを記載します。my_or_tools.pyやtableutils.py
の中身に関しては著者GitHubをご覧ください。
from my_or_tools import ObjVal, SolVal, newSolver
def solve_model(D):
s = newSolver('Project management') #ソルバーを宣言
n = 12 #タスク数
max = sum(D[i][1] for i in range(n)) #決定変数の上限を計算
t = [s.NumVar(0,max,'t[%i]' % i) for i in range(n)] #決定変数。タスクiの開始時間
Total = s.NumVar(0,max,'Total') #終了時刻。今回最小にしたい。
for i in range(n):
s.Add(t[i]+D[i][1] <= Total) #目的関数が満たすべき制約
for j in D[i][2]:
s.Add(t[j]+D[j][1] <= t[i]) #先行タスクに関する制約
s.Minimize(Total)
rc = s.Solve()
return rc, SolVal(Total),SolVal(t)
Data = [ [0, 3, []], #例題のデータ
[1, 6, [0]],
[2, 3, []],
[3, 2, [2]],
[4, 2, [1,2,3]],
[5, 7, []],
[6, 7, [0,1]],
[7, 5, [6]],
[8, 2, [1,3,7]],
[9, 7, [1,7]],
[10, 4, [7]],
[11, 5, [0]] ]
def main():
import sys
import tableutils
n = len(Data)
C = Data
if sys.argv[1]=='data': #引数がdataならデータを表示
T=[]
for i in range(n):
TT=[C[i][0],C[i][1]]
s='{'
for j in C[i][2]:
s = s+' '+str(j)
s=s+' }'
TT.append(s)
T.append(TT)
T.insert(0,['Task', 'Duration','Preceding tasks'])
tableutils.printmat(T,True)
elif sys.argv[1]=='run': #引数がrunなら実行結果を表示
rc,V,G=solve_model(C)
T=[]
TT=['Task']+[C[i][0] for i in range(n)]
T.append(TT)
TT=['Start']+[int(G[i]) for i in range(n)]
T.append(TT)
TT=['End']+[int(G[i]+C[i][1]) for i in range(n)]
T.append(TT)
tableutils.printmat(T,True)
main()
結果
上記のコードで以下の最適解が求まります。
| タスク | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 開始時刻 | 0 | 3 | 0 | 3 | 9 | 0 | 9 | 16 | 26 | 21 | 24 | 23 |
| 終了時刻 | 3 | 9 | 3 | 5 | 11 | 7 | 16 | 21 | 28 | 28 | 28 | 28 |
| 表から分かる通り、最短の終了時刻は28です。 | ||||||||||||
| スケジュール表を作ると以下のようになります。 |
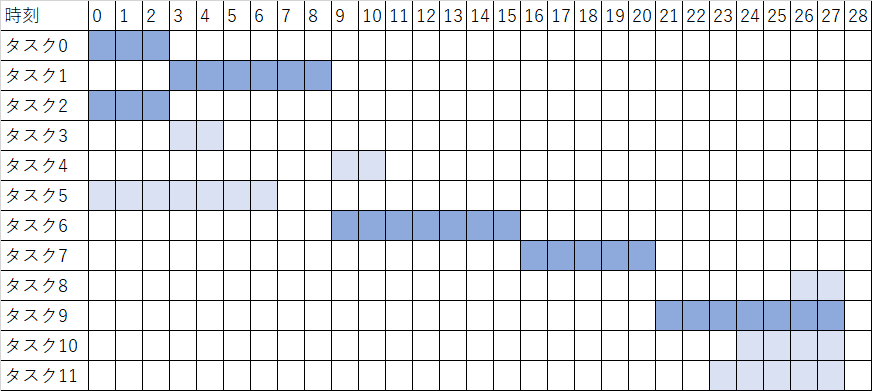
ここで注意しなければならないのは、先行タスクの後でさえあればいつ始めても全体の作業時間に影響しないタスクもあることです。
タスク11なんかは、先行タスクのタスク0が時刻3で終わっているにも関わらずギリギリに始めることになっています。実は今回の定式化ではソルバーによって最適解が変わります。(作業時間の最適値は変わりません)
別の解とスケジュール表を以下に示します。
| タスク | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 開始時刻 | 0 | 3 | 0 | 3 | 9 | 0 | 9 | 16 | 21 | 21 | 21 | 3 |
| 終了時刻 | 3 | 9 | 3 | 5 | 11 | 7 | 16 | 21 | 23 | 28 | 25 | 8 |
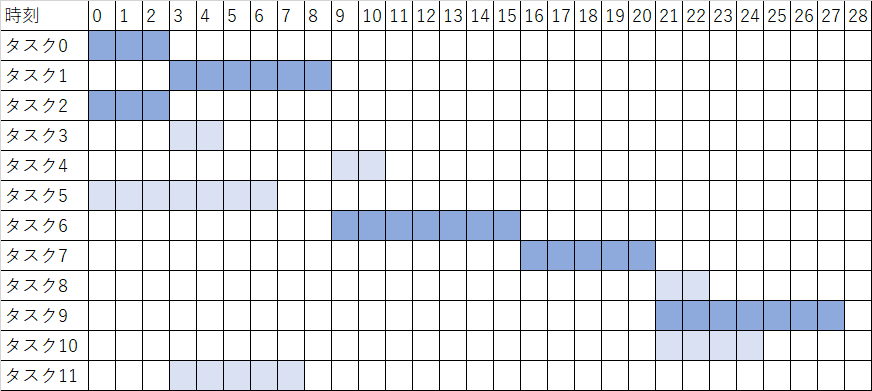 |
下の方のタスクが少し左にズレましたね。先行タスクが終わっている限り、タスクは可能な限り早く始めた方が実用的です。プロジェクトが予定通りに進むことはほとんどなく、後者の方が何かあった時に全体の作業時間が延びるリスクが低いためです。
表で濃い色にしたタスク(0,2,1,6,7,9)は、クリティカルパスになっています。簡単に言うと、このどれか一つでも遅れると全体の作業時間が延びるということです。今回の例では表を作れば一目瞭然ですが、工程の多い大きなプロジェクトだとそうはいきません。クリティカルパスを計算する方法についても今後取り扱おうと思います。
タスクをなるべく早く始める解を出すには
s.Minimize(Total)となっている行をs.Minimize(sum(t[i] for i in range(n)))と書き換えればOKです。
まとめ
たかし君はカレーライスを最短で作るための手順を見つけることに成功しましたが、主婦歴15年のお母さんは一つ一つのタスクの所要時間がたかし君より短いため余裕で負けましたとさ。