1. はじめに
千円程度で購入できるCTセンサとESP32を用いて,電力の簡易計測を行ってみます.あくまで参考値レベルの精度ですので,厳密な値が必要な場合は市販のメータを利用する方が良いでしょう.
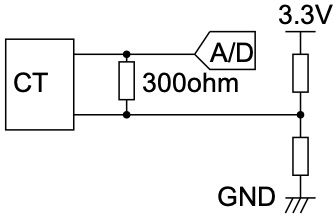
2. 回路
CTセンサとESP32と抵抗3本を用います. 抵抗は300Ω1本,1kΩ2本です. 300ΩはCTセンサの負荷抵抗で, ラジオペンチ様のブログを参考にさせて頂きました.
1kΩは分圧して中点にしています.

3. コード
ちょっと汚いですが...
(50Hz地域用です)
CTsensor.ino
# define PIN_MIC_IN 33
# define MICROSEC_INTERRUPT_INTERVAL 100 //100=10kSa/s //22kHz=45
# define MAX_SIZE 8*1024 //1024//16*1024
# define NUM_PREREAD_SIZE (MAX_SIZE/4) //2048
unsigned int guiStream[MAX_SIZE];
volatile unsigned int guiCountReadAdc=0;
volatile unsigned int guiPreRead=0;
float gfValAve=0;
# define FREQ_POWER_LINE 50
# define N_SAMPLE_POWER_CYCLE (int)(1000*1000/( MICROSEC_INTERRUPT_INTERVAL * FREQ_POWER_LINE ))
# define PI (double)(3.14159265358979323846)
float gfCosTable[N_SAMPLE_POWER_CYCLE];
float gfSinTable[N_SAMPLE_POWER_CYCLE];
# define COEF_IIR_ALPHA (float)0.8
# define COEF_IIR_BETA (1-COEF_IIR_ALPHA)
# define PARAM_RESISTOR 300
# define PARAM_VOLTAGE_RMS 100
# define PARAM_ADC_MAX (float)3.3
# define PARAM_RATIO_CT 3000
# define PARAM_ADC_BITWIDH 12
//#define FACT_POW (3.3*3000/300*100/(float)(1<<12) )
# define FACT_POW (PARAM_ADC_MAX*PARAM_RATIO_CT*PARAM_VOLTAGE_RMS/(PARAM_RESISTOR*(float)(1<<PARAM_ADC_BITWIDH)) )
# define FACT_CUR (PARAM_ADC_MAX*PARAM_RATIO_CT/(PARAM_RESISTOR*(float)(1<<PARAM_ADC_BITWIDH)) )
hw_timer_t *timer1 = NULL;
volatile SemaphoreHandle_t timerSemaphore;
portMUX_TYPE timerMux = portMUX_INITIALIZER_UNLOCKED; //rer to https://techtutorialsx.com/2017/10/07/esp32-arduino-timer-interrupts/
void IRAM_ATTR onTimer1() {
portENTER_CRITICAL_ISR(&timerMux);
guiStream[guiCountReadAdc] = analogRead(PIN_MIC_IN);
if (guiCountReadAdc < (MAX_SIZE-0) ){
guiCountReadAdc += 1;
}
portEXIT_CRITICAL_ISR(&timerMux);
xSemaphoreGiveFromISR(timerSemaphore, NULL);
}
void makeTable(){
float fOmega=0;
for(int uilp=0;uilp<N_SAMPLE_POWER_CYCLE;uilp++){
fOmega = (float)(2*PI*(float)uilp/(float)N_SAMPLE_POWER_CYCLE);
gfCosTable[uilp] = cos(fOmega);
gfSinTable[uilp] = sin(fOmega);
}
}
void setup() {
Serial.begin(115200);
pinMode(PIN_MIC_IN, INPUT);
timerSemaphore = xSemaphoreCreateBinary();
timer1 = timerBegin(0, 80, true);
timerAttachInterrupt(timer1, &onTimer1, true);
timerAlarmWrite(timer1, MICROSEC_INTERRUPT_INTERVAL , true);//us
timerAlarmEnable(timer1);
guiCountReadAdc=0;
guiPreRead=0;
gfValAve=0;
makeTable();
unsigned int uiFlag=0;
while(uiFlag==0)
{
if (xSemaphoreTake(timerSemaphore, 0) == pdTRUE) {
portENTER_CRITICAL(&timerMux);
if(guiCountReadAdc>NUM_PREREAD_SIZE){
uiFlag=1;
guiPreRead=1;
}
portEXIT_CRITICAL(&timerMux);
}//endif xSemaphore
}
//Serial.println("start sampling");
}
void loop()
{
unsigned int uiCounterVal=0;
if (xSemaphoreTake(timerSemaphore, 0) == pdTRUE) {
portENTER_CRITICAL(&timerMux);
uiCounterVal = guiCountReadAdc;
portEXIT_CRITICAL(&timerMux);
}//endif xSemaphore
if ( uiCounterVal >= (MAX_SIZE-1) ){
timerAlarmDisable(timer1);
float fMean=0;
float fDiff=0;
float fSum=0;
fMean = calc_mean();
float fRms = calc_rms(fMean);
float fFund = calc_fundamental(fMean);
//float fPow = fRms * FACT_POW * fFund;
float fPow = FACT_POW * fFund;
Serial.print(fPow);
Serial.print(" , ");
Serial.println(fRms*FACT_CUR);
guiCountReadAdc=0;
timerAlarmEnable(timer1);
}//endif counter
}
float calc_mean(void){
float fMean=0;
for(unsigned int uilp =0;uilp<(MAX_SIZE-1);uilp++){
fMean += (float)guiStream[uilp];
}//end for
fMean = fMean/(float)(MAX_SIZE-1);
return(fMean);
}
float calc_rms(float fMean){
float fDiff=0;
float fSum=0;
for(unsigned int uilp =0;uilp<(MAX_SIZE-1);uilp++){
fDiff = (float)guiStream[uilp]-fMean;
fSum += fDiff*fDiff;
}//end for
float fRms = sqrt(fSum/(float)(MAX_SIZE-1));
return(fRms);
}
# define N_DFT_LOOP_INT (int)((MAX_SIZE-1)/N_SAMPLE_POWER_CYCLE)
# define N_DFT_LOOP_TAIL (int)(MAX_SIZE-1 - N_DFT_LOOP_INT*N_SAMPLE_POWER_CYCLE)
float calc_fundamental(float fMean){
float fSumR=0;
float fSumI=0;
float fTmp=0;
float fSumP=0;
unsigned int uiinx=0;
for(unsigned int uic = 0;uic < N_DFT_LOOP_INT ; uic++){
for(unsigned int uilp =0;uilp<(N_SAMPLE_POWER_CYCLE);uilp++){
fTmp = ((float)guiStream[uiinx]-fMean);
fSumR += gfCosTable[uilp]*fTmp;
fSumI += gfSinTable[uilp]*fTmp;
uiinx++;
}//end for uilp
}//end for uic
for(unsigned int uilp =0;uilp<(N_DFT_LOOP_TAIL);uilp++){
fTmp = ((float)guiStream[uiinx]-fMean);
fSumR += gfCosTable[uilp]*fTmp;
fSumI += gfSinTable[uilp]*fTmp;
uiinx++;
}//end for uilp
float fFund = sqrt( (fSumR*fSumR+ fSumI*fSumI)*2)/(float)(MAX_SIZE-1) ;
return(fFund);
}
4. プログラムの解説
プログラム自体は難しいことはしてません.計算が少し厄介なので,後で説明します.
- 50Hz正弦波テーブル作成(60Hz地域は要変更)
- タイマー割り込みで電流値を一定間隔でサンプリング
- 電流波形から正弦波テーブルを用いて基本波成分を計算
- Vrms=100Vとかけ算して有効電力を算出し,表示
5. 計算の経緯について
5.1. 電力とは
P: 電力,V: 電圧, I:電流 ,とすると
$$
P = V\cdot I
$$
となります.
日本では普通の電源は,V=100[V]なので," I "が判れば電力が求められる...はずが,
試しに,ディスプレイの電力を求めようと,根本にクランプセンサを付けて,電流のRMSを求めて100をかけてもワットチェッカーと同じ値になりません. ワットチェッカーは15.9[W]で,算出されたのは28.0[W]と誤差76%でした.
何故か?
5.2. 有効電力とは
P: 有効電力,v(t): 電圧, i(t):電流
$$
P = \frac{1}{T} \int ^T_0 v(t) \cdot i(t) dt
$$
です.
つまり,v(t)は測定しなければ正しい有効電力は求められません.
と,いうことで,今回の回路では,有効電力は求めることが出来ません.
残念...と諦めてはつまらないので,なんとか近似値を出す方法を考えましょう.
5.3. 歪み波の有効電力測定
次のページが参考になります.
交流電力の基礎知識と電力測定器の仕組み(横河電機)
ディスプレイの電流波形は歪んでいます.一般的にLED照明の電流波形は歪んでいることが多いです.
電圧波形と電流波形に高調波が含まれているとします.
$$
v(t) = V_0 + \sum ^{ \infty } _{n=0} \cdot \cos( n \cdot \omega _n \cdot t - \theta _n)
$$
$$
i(t) = I_0 + \sum^{\infty}_{n=0} I_n \cdot \cos(n\cdot \omega _n \cdot t - \theta _n)
$$
これらを有効電力の定義に代入し,
$$
P = V_0 \cdot I_0 + \sum^{\infty}_{n=0} V_n \cdot I_n \cdot \cos(\phi_n)
$$
となるとされています. (Φは位相差)
この式は,異なる周波数成分の電圧と電流の積の平均がゼロになることを示しています.
電圧の高調波が無い(無歪み)場合,電流の高調波成分をかけてもゼロになります.
よって有効電力は,
$$
P = V_0 \cdot I_0
$$
となります.
つまり,電流の基本波成分のみを求め,電圧のRMS値である100Vをかけると,有効電力が求められます.
6. むすび
今回の方法で電力を算出すると,15[W]弱と誤差も数%になりました. ただし,これは測定対象が力率改善回路が入っているという前提になります. 力率が大きく異なると, 有効電力も大きく差が出ます. しかし,この10年でLEDもすっかり普及し,力率改善回路も普通に導入されるようになりました.なので,今回の手法で参考になる値は求められるのではと考えています.
ところで,LEDの普及は,2010年前後でのパワーエレクトロニクスの進歩と共に進んだように感じます.当時は,電力効率化はとても重要なテーマでした.そして,2011年の東日本大震災で,原発が止まり,電力消費量はとても注目されるようになりパワーエレクトロニクスがより一層注目されました.しかし,次第に忘れそうになった2020年,再び,脱炭素というキーワードが挙がるようになりました.脱炭素には,エネルギー効率の改善と省エネが重要だろうと思います.
電力を測定することで,省エネを心がけるきっかけになればと思います.