やること
ここでは欧州原子核研究機構CERNが開発しているROOTについて記述します。
今回はヒストグラム(Histogram)の一連の操作を記述しようと思います。
内容は以下の通りです。
- ヒストグラムを定義する
- ビンを調整する
- 関数でフィットする
- ヒストグラムの演算操作
- ヒストグラムを積み重ねる
公式のクラスページを参考にしています。
ヒストグラムを定義する
ROOTでは1次元、2次元、3次元それぞれに応じたヒストグラムのクラスが用意されています。
また、変数が自然数なのか、浮動小数なのかといった特徴に応じて、クラスがさらに細かく分かれています。
基本的にTH1Fを使っておけばよいと思います。簡単な例を使ってどんなことができるのかみてみましょう。
サンプル
from ROOT import TCanvas, TH1F, TRandom
rdm = TRandom()
rdm.SetSeed(1)
c = TCanvas()
# ヒストグラムを定義
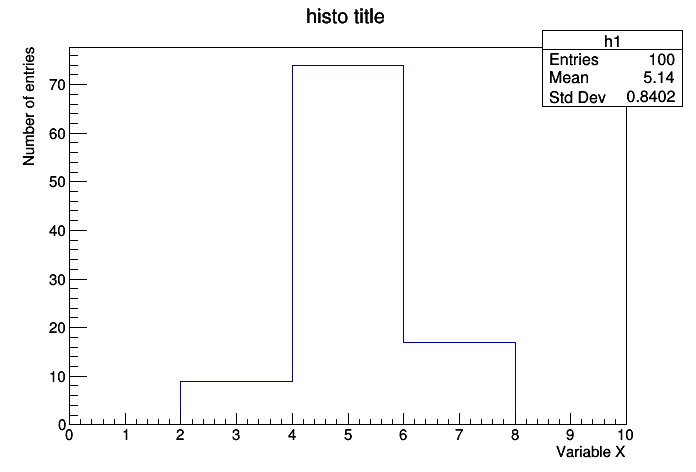
h = TH1F("h1", "histo title;Variable X;Number of entries", 10, 0, 10)
# ガウス分布にしたがって発生させた乱数をヒストグラムに詰める
for i in range(100):
h.Fill( rdm.Gaus( 5, 1) )
# ヒストグラムを描画
h.Draw()
c.SaveAs("test-1.png")
このプログラムで下図が出力されます。
解説
ヒストグラムの定義部分に注目。
h = TH1F("h1", "histo title;Variable X;Number of entries", 10, 0, 10)
引数は次の通り。
- 1つ目(
"h1"): ヒストグラム自体の名前 - 2つ目(
"histo title;Variable X;Number of entries"):タイトル、X軸のタイトル、Y軸のタイトルをセミコロンで分けて書いています。
それぞれのタイトルをh.SetXTitle("Variable X")このように個別に設定することもできます。 - 3つ目(
10):ビンの数。横軸の最小値(0)から最大値(10)までを10個のビンに分割しています。 - 4つ目(
0):横軸の最小値 - 5つ目(
10):横軸の最大値
ビンを調整する
もっとビンの幅を大きくしたい!というときにはRebinを使うと便利。
例えば、今回の場合h.Rebin(2)をfor文の後に書いておくと、
下図のようにビンの幅が2倍(ビンの数は半分)になります。
上の例では、最小値から最大値まで均等なビンでデータを表示していますが、状況によっては不均等なビンで表示したい場合もあります。
この場合は、ビニングを表す配列を用意しておいて、Rebinの引数に渡せばOK。
たとえば、
bin_array = array.array('d',[0., 3., 5., 6., 7., 10.])
h2 = h.Rebin(5, "h2", bin_array)
h2.Draw()
とすれば、次のように不均等のビンで描画できます。ここで、ファイル内でimport arrayしてます。
関数でフィットする
ヒストグラムを表示したあと、どのような関数に従っているのか知りたいことがあります。
そのようなときは、関数でヒストグラムをフィットすることである程度知見を得られます。
ここではガウス分布でヒストグラムをフィットさせたいと思います。
サンプル
以下、サンプルコードです。
from ROOT import TCanvas, TH1F, TRandom, TF1, TMath
rdm = TRandom()
rdm.SetSeed(1)
c = TCanvas()
h = TH1F("h1", "histo title;Variable X;Number of entries", 10, 0, 10)
#
for i in range(100):
h.Fill( rdm.Gaus( 5, 1) )
#
h.Draw()
# フィット関数を定義
f = TF1("f", "[0]*TMath::Gaus(x, [1], [2])", 0, 10)
# テキトーなパラメタを設定
f.SetParameters(1, 1, 1)
# ヒストグラムにフィット
h.Fit(f, "", "", 0, 10)
c.SaveAs("test-4.png")
このコードを実行すると、ターミナル上に次のようなログが出力されます。
[centos@ip-10-0-1-72 part2]$ python test2-4.py
FCN=1.13064 FROM MIGRAD STATUS=CONVERGED 126 CALLS 127 TOTAL
EDM=4.14811e-09 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 2.6 per cent
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 4.33920e+01 5.26777e+00 5.85071e-03 1.66271e-05
2 p1 5.09095e+00 9.56735e-02 1.33674e-04 7.93763e-04
3 p2 9.16954e-01 6.74583e-02 -3.97008e-05 -3.05272e-05
Info in <TCanvas::Print>: png file test-4.png has been created
このようにフィット結果の統計情報とパラメタの値などが表示されます。
出力した図は次の通り。
赤い曲線がフィット結果のガウス分布です。
簡単に結果を得られました。
解説
フィット関数の定義
コード上ではTF1というクラスを使って、関数を定義しています。
f = TF1("f", "[0]*TMath::Gaus(x, [1], [2])", 0, 10)
引数は次の通り。
- 1つ目(
"f"):この関数の名前。テキトーにつける。 - 2つ目(
"[0]*TMath::Gaus(x, [1], [2])"):関数を定義。 今回はガウス分布でフィットしてみたかったので、TMathというクラスのガウス関数を使っています。1つ目の引数は横軸を表す"x"、2つ目は平均値、3つ目は標準偏差です。他の関数や詳細についてはこちら。カギカッコの数字がフィットで求めるパラメタを表します。つまり、規格化定数がパラメタ0、平均値がパラメタ1、標準偏差がパラメタ2となります。 - 3つ目(
0):関数を定義する区間の最小値。 - 4つ目(
10):関数を定義する区間の最大値。
フィットパラメタの初期値
関数を定義した後、下のように初期パラメタをセットしました。
f.SetParameters(1, 1, 1)
今回はテキトーに全パラメタの値を1で初期化していますが、初期化しないとフィットに失敗することがあるので、なんでも設定しておくことが大事です。
ヒストグラムのフィット
h.Fit(f, "", "", 0, 10)
この引数については次の通り。
- 1つ目(
f):フィット関数を指定。 - 2つ目(
""):フィットのオプションを指定。詳しくはこちら。"NQ0"のように複数指定することもできる。最小化アルゴリズムを指定することもできる。 - 3つ目(
""):フィットのグラフィカルオプションを指定。あまり指定したことない... - 4つ目(
0):フィット区間の最小値 - 5つ目(
10):フィット区間の最大値
今回はデフォルトでTF1のフィット後の関数が自動的に描画されていますが、f.Draw()のように明示的に指定してもOK。
フィット関数はTMathで用意されているものを使っていますが、sin(x)+cos(x)のように複数組み合わせたり、自分でオリジナルの関数を作って使用することもできる。
ヒストグラムの演算操作
ROOTではヒストグラムを定数や関数で足し引きしたり、掛け算もできる。
また、ヒストグラム同士で演算できる。
コードは次の通り。
from ROOT import TCanvas, TH1F, TRandom, TF1, TMath
rdm = TRandom()
rdm.SetSeed(1)
c = TCanvas("c", "c", 1200, 300)
c.Divide(4,1)
h1 = TH1F("h1", "histo title;Variable X;Number of entries", 10, 0, 10)
#
for i in range(100):
h1.Fill( rdm.Gaus( 5, 1) )
#
h2 = h1.Clone("h2")
h3 = h1.Clone("h3")
# 定数関数を定義。y = 10
fconst = TF1("fconst", "[0]", 0, 10)
fconst.SetParameter(0, 10)
c.cd(1)
h1.SetTitle("Original")
h1.Draw()
c.cd(2)
h2.SetTitle("+10")
h2.Add(fconst, 1, "") #h2 = h2 + 1*fconst
h2.Draw()
c.cd(3)
h3.SetTitle("-10")
h3.Add(fconst, -1, "") #h3 = h3 + (-1)*fconst
h3.Draw()
c.cd(4)
h4 = h2.Clone("h4") # h2をh4として複製
h4.SetTitle("(h+10)+(h-10)")
h4.Add(h3) # h4 = h4 + h3
h4.Draw()
c.SaveAs("test-5.png")
コード上のAddという関数をつかって、定数関数のfconstを足し引きしてます。
これを実行すると、次のような図が出力されます。
一番左はもとのヒストグラム。左から2番目は定数で10だけ足したもの、3番目は定数で10だけ引いたもの。
一番右は、2番目と3番目をのヒストグラムを足し合わせたものです。
同様に、Multiplyという関数を使えば掛け算を、Divideという関数を使えば割り算をすることができます。
ヒストグラムを積み重ねる
複数のヒストグラムを積み重ねて表示したいときもあります。
そのようなときはTHStackを使うと便利です。
from ROOT import TCanvas, TH1F, TRandom, THStack, TColor
import ROOT
rdm = TRandom()
rdm.SetSeed(1)
c = TCanvas("c", "c", 600, 600)
c.Divide(2,2)
h1 = TH1F("h1", "h1;Variable X;Number of entries", 10, 0, 10)
h2 = TH1F("h2", "h2;Variable X;Number of entries", 10, 0, 10)
# THStackを定義
hs1 = THStack("hs1", "THStack;Variable X;Number of entries")
# ヒストグラムの色を設定
h1.SetLineColor(ROOT.kRed+1)
h1.SetFillColor(ROOT.kRed+1)
h2.SetLineColor(ROOT.kBlue+1)
h2.SetFillColor(ROOT.kBlue+1)
#
for i in range(100):
h1.Fill( rdm.Gaus( 5, 1) )
h2.Fill( rdm.Gaus( 1, 2) )
# THStackにヒストグラムを詰める
hs1.Add(h1)
hs1.Add(h2)
c.cd(1)
h1.Draw()
c.cd(2)
h2.Draw()
c.cd(3)
hs1.Draw()
c.cd(4)
hs1.Draw("nostackb")
c.SaveAs("test-6.png")
このコードを実行すると、下図が出力されます。
上の2つがヒストグラムh1とh2をそれぞれ表示してます。
左下は、h1とh2を積み重ねたTHStackを表示したもの。右下はTHStackの表示オプションを"nostackb"に指定して表示したもの。