Easier timegates for beginners coming to Bemuse

Abstract: Bemuse introduces an easier set of timegates, determined from statistical data of past 60000 games played on Bemuse, which will be applied to charts with level 1~5. Charts at level 6+ are not affected by this change.

Introduction

Bemuse has very strict timegates. More strict than LR2’s EASY judge (which most BMS uses):

Judgment	Bemuse	LR2 #RANK 3
Meticulous / PGreat	20ms	21ms
Precise / Great	50ms	60ms
Good / Good	100ms	120ms
Offbeat / Bad	200ms	200ms

However, this makes this game very unfriendly for beginners.

Analyzing the impact of the problem

I analyzed the data of about 60,000 games played on Bemuse.

Assuming that beginners play level-1 songs (7,000 games), here is the distribution of the given grades:

Grade	Minimum Score	Percentage
F	0	35%
D	300000	15%
C	350000	18%
B	400000	19%
A	450000	10%
S	500000	3%

68% of all the level-1 games ended with bad grades (F, D, C). Getting bad grades all the time is quite demotivating for new players.

First proposal

First, I put a proposal to add beginners timegates with the following thresholds:

Judgment	Normal	Beginner
Meticulous	20ms	50ms
Precise	50ms	100ms
Good	100ms	160ms
Offbeat	200ms	200ms

The beginner timegates would be applied on level-1 and level-2 songs.

I chose to adjust the timegates over other options because:

• I don’t want to introduce options (e.g. adding a beginner mode) as that would complicate the game and the scoreboard.

• I don’t want to adjust the grading threshold as that would make the grading scheme inconsistent. I prefer to be able to say “If you get more than 450,000 you get an A” regardless of levels or settings.

Therefore, I decided to inflate the score for beginner charts, so that they get good grades easier, while retaining the rest of the game mechanics.

Feedback

I received several initial feedback from people in the BMS Chat Discord group:

• People would have hard time adapting to normal timegates when it is suddenly 2.5x smaller.

• Changing the timegates at level-3 seems too sudden. A more gradual transition may be better.

• Some people are not sure whether forcing an easier timegates on easier charts is a good idea or not.

Also:

• It will be very easy to get a full perfect score (555555). The scoreboard will be filled with the same scores if the meticulous timegate is too wide.

Several ideas are suggested:

• Gradual increase in difficulty. As level increases, make the timegates stricter.

• Separate beginner mode.

• Binary judging (e.g. only Meticulous and Offbeat/Missed).

The plan forward

I decided to implement gradual increase in difficulty up to level 5, so that it does not affect any players playing level 6 and above.

I decided not to implement a separate mode due to the reasons listed in the previous section. Also, I decided not to do binary judging as that would result in many people ending up getting the same score (I try to avoid that).

So, I decided to implement 5 sets of timegates:

• Beginner timegates for songs at level 1 and 2.
• Level3 timegates for songs at level 3.
• Level4 timegates for songs at level 4.
• Level5 timegates for songs at level 5.
• Normal timegates for songs at level 6+.

But what numbers should I use for these sets of timegates?

Let’s understand the behavior of players more.

Segmenting the users

I obtained the table of scores at the 1st, 2nd and 3rd quartile for each level.

Note: Level 0 is the tutorial.

Level	Q1	Q2	Q3	Average	n(Games)
0	104686	154259	268021	198136	2765
1	252622	346444	414653	327137	7336
2	322991	381918	426359	366219	2560
3	324557	381131	427655	368571	4374
4	320880	385333	438184	371018	4677
5	329700	388028	436259	375340	5827
6	341833	397973	443670	385106	5423
7	354577	411894	452297	392514	5189
8	377016	421752	456300	408947	4247
9	377461	429192	466141	415859	5267
10	379397	431703	469782	416676	5373
11	400372	443042	474009	428015	2611
12	399461	437981	469937	422399	3610

Then I decided 5 personas:

• Beginners: Level-1 games that scored between Q1~Q2 (252622~346444).
• Level3: Level-3 games that scored between Q1~Q2 (324557~371131).
• Level4: Level-4 games that scored between Q1~Q2 (320880~385333).
• Level5: Level-5 games that scored between Q1~Q2 (329700~388028).
• Normal: Level-8 games that scored between Q1~Q3 (377016~456300).

This allows me to take a closer look at each persona.

The accuracy data

Along with each game’s score, Bemuse also collects the accuracy data, which is a histogram of note offsets.

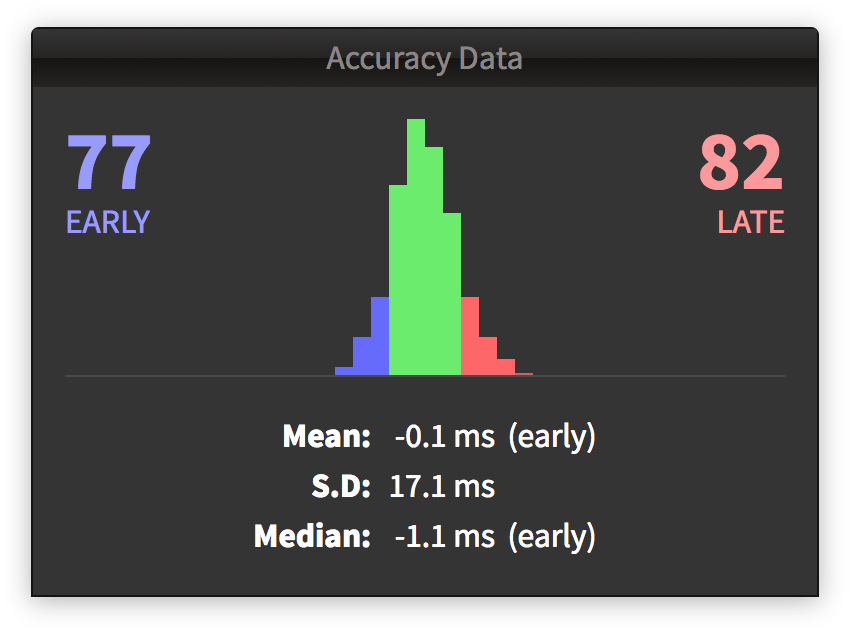
Note offsets generally follows a normal distribution curve. So, by looking at the S.D. (standard deviation) number we could approximate the accuracy. We assume that the mean is 0ms.

First, start with the S.D. value itself:

$$ \sigma = 17.1\text{ms} $$

Calculate the probability that a note would receive a certain judgment, according to the Normal judge:

$$
\begin{align*}
P[Meticulous] & = 2(\Phi(0) - \Phi(-\frac{20\text{ms}}{\sigma})) = 75.8% \\
P[Precise] & = 2(\Phi(-\frac{20\text{ms}}{\sigma}) - \Phi(-\frac{50\text{ms}}{\sigma})) = 23.9% \\
P[Good] & = 2(\Phi(-\frac{50\text{ms}}{\sigma}) - \Phi(-\frac{100\text{ms}}{\sigma})) = 0.3%
\end{align*}
$$

Combine those probabilities to obtain the expected accuracy:

$$
\begin{align*}
E[Accuracy] & = P[Meticulous] + (0.8) P[Precise] + (0.5) P[Good] \\
& = 95.1%
\end{align*}
$$

Which is quite close to the actual accuracy score reported by the game, 95.07%.

Therefore, the S.D. represents how precise the player is able to hit those notes, independent of the timegates used. The lower the S.D., the more precise.

Data of each persona

Next, we look at each persona, and find out:

• The average S.D. (used to approximate the timegates-independent accuracy).
• The average combo bonus score (used to determine expected final score).

Here is the resulting data:

Persona:	Normal	Level5	Level4	Level3	Beginner
E[S.D.]	38ms	50ms	52ms	52ms	64ms
E[Combo bonus]	21340	14752	15009	14800	19912

Then we calculate the grade a persona would get under the Normal judge:

Persona:	Normal	Level5	Level4	Level3	Beginner
P[Meticulous]	40.1%	31.1%	29.9%	29.9%	24.5%
P[Precise]	41.0%	37.2%	36.4%	36.4%	32.0%
P[Good]	18.0%	27.2%	28.2%	28.2%	31.6%
E[Accuracy]	82.0%	74.4%	73.2%	73.2%	66.0%
E[Score]	431112	386685	380897	380768	349705
E[Grade]	B	C	C	C	D

Devising a new judgment scheme

Next, I devised a judgment scheme with the following constraints:

1. For each persona, the expected grade should be B. Expected final score should be 400000~450000.

2. It should still be impractical for experts to get a perfect score on beginner songs. The probably of obtaining a perfect score by an expert should stay below 1%.

For this, we need another persona: the Expert persona, which represents the games that scored over 540000. About 100 games were found, so this persona represents the top 0.16% of all the games. This persona have a S.D. value of 12 ms average.

For beginner songs, we calculate the chance of getting a perfect score by calculating the probability in which this persona would get 100 consecutive Meticulous judgments, $P[Meticulous]^{100}$.

For $P[Meticulous]^{100}$ to stay below 1%, the Meticulous timegate should be no more than 24ms.

With this constraints, it’s time to tweak the knobs!

Result

I played around with different numbers until I came up with this judgment scheme:

Judgment	Normal	Level5	Level4	Level3	Beginner
Meticulous	20ms	21ms	22ms	23ms	24ms
Precise	50ms	60ms	70ms	80ms	100ms
Good	100ms	120ms	140ms	160ms	180ms
Offbeat	200ms	200ms	200ms	200ms	200ms
E[Score]	431112	408684	419273	429940	430191
E[Grade]	B	B	B	B	B

These sets of timegates will hopefully make Bemuse easier for beginners, while retaining the difficulty in the most part.